Алгоритмы определения комплексного коэффициента передачи в системах автоматизированного контроля качества пьезоэлементов.

Воронов Александр Сергеевич,

кандидат технических наук,

Цуриков Виталий Сергеевич,

аспирант кафедры_Информационных технологий,

Алтайский_Государственный Технический_Университет им. И.И. Ползунова.

На сегодняшний день пьезоэлементы используются во многих областях науки и техники: промышленные датчики, двигатели наноперемещений, биморфные зеркала, генераторы, линии задержки и т.д. [1-5]. Малейшие погрешности при изготовлении пьезоэлементов приводят к существенному изменению их эксплуатационных параметров. Следовательно, повышение эффективности контроля качества пьезоэлементов является актуальной задачей.   Наиболее информативным параметром используемым для контроля качества  является комплексный коэффициент передачи пьезоэлемента (ККПП) [7]. Этот параметр представляет собой полную динамическую характеристику и устанавливает однозначную зависимость между электрическим сигналом, поданным на пьезоэлемент, и колебанием его поверхности. Поскольку амплитуда колебаний поверхности пьезоэлемента находится в диапазоне 10^-9…10^-6 м. определение ККПП является нетривиальной задачей.

Для практического определения комплексного коэффициента передачи предложена оптико-электронная измерительная система [6, 7], функциональная схема которой представлена на рисунке 1. На рисунке отражены следующие характеристики: ,  - спектры сигналов на выходе ЦАП1 и ЦАП2; ,  - спектры сигналов на входе АЦП1 и АЦП2; ,  - комплексный коэффициент передачи фильтров на выходе ЦАП1 и ЦАП2; ,  - комплексный коэффициент передачи фильтров на входе АЦП1 и АЦП2;  - ККПП;  - комплексный коэффициент передачи оптико-электронного преобразователя.

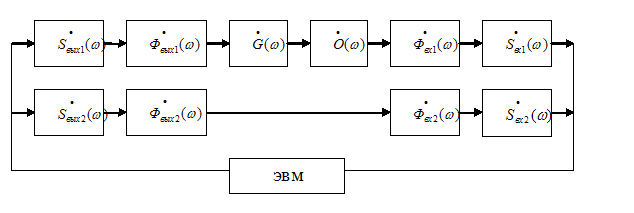
Рисунок 1.

Функциональная схема оптико-электронной системы.

Такая система удобна при использовании АЦП с фильтром на входе и ЦАП с фильтром на выходе. Два идентичных канала позволяют избежать дополнительных вычислений за счет компенсации характеристик АЦП, ЦАП и соответствующих фильтров.

Согласно рисунку 1 вычисление ККПП выглядит следующим образом:

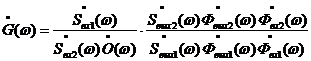.    (1)

Поскольку сигнал на выходе обоих каналов одинаков = и соответствующие фильтры идентичны =,  =, то формула (1)  упрощается:

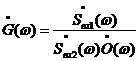.                                              (2)

Оптическая составляющая  в формуле (2) характеризует инертность оптико-электронного преобразователя. Если на интересующем нас диапазоне частот  , что было доказано при моделировании, то имеет место безинерционный оптико-электронный преобразователь:

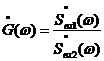.                                                       (3)

Формула (3) является базовой формулой для вычисления ККПП с использованием предложенной измерительной системы. Как говорилось ранее, ,  - комплексные спектры сигнала на входе АЦП1 и АЦП2, однако на практике мы  имеем дело с временным а не спектральным представлением, что обуславливает необходимость алгоритмического обеспечения, позволяющего восстановить амплитудный и фазовый спектры, как составляющие комплексного спектра сигнала.

Классическим методом, позволяющим осуществить переход от временной к частотной области, является использование прямого дискретного преобразование Фурье (ДПФ). Условия, которым должен удовлетворять выходной сигнал, пригодный для последующего преобразования в измерительной системе и анализа при помощи прямого ДПФ формулируются следующим образом. Сигнал должен быть вида:

,                                     (4)

где I – количество гармоник, Ti – период каждой гармоники в отсчетах, кратный количеству отсчетов входного сигнала К -  , d=1…K. Для точного восстановление спектра  с малым шагом по частоте необходимо использовать достаточно длинную выборку сигнала, с многократным прямым ДПФ этой выборки, выборки размера K-1, выборки размера K-2 … и т.д. Такой подход с одной стороны позволяет избежать эффекта растекания спектра, с другой исключает главное преимущество ДПФ, достигнутое на сегодняшний день – производительность. Это объясняется тем, что размер выборки переменный и не всегда может быть кратен степени 2, что не позволяет использовать быстрое преобразование Фурье. Правда, существуют модификации БПФ для разных размеров выборки: степени 2, степени 3, четного числа, нечетного числа и т.д., тем не менее, даже с использованием этих алгоритмов остается проблема многократного их применения на одну и туже выборку уменьшающегося размера. Если предположить, что количество операций для каждой выборки будет такое же, что и для выборки, размер которой кратен степени 2, то общее количество операций для выборки размером K будет определяться как:

.                                                        (5)

Используя формулу (5) для относительно небольшого размера выборки в 1024 отсчета, получим около пяти миллионов операций. Такой результат позволяет сделать два важных вывода.

1. Если требования к шагу по частоте низкие и укладываются в требования к формуле (4) либо необходимо получить только амплитудный спектр, то прямое ДПФ может быть рекомендовано для анализа.

2. В случае невозможности выполнения условий к формуле (4), необходимо использовать другие алгоритмы, позволяющие определить спектр сигнала.

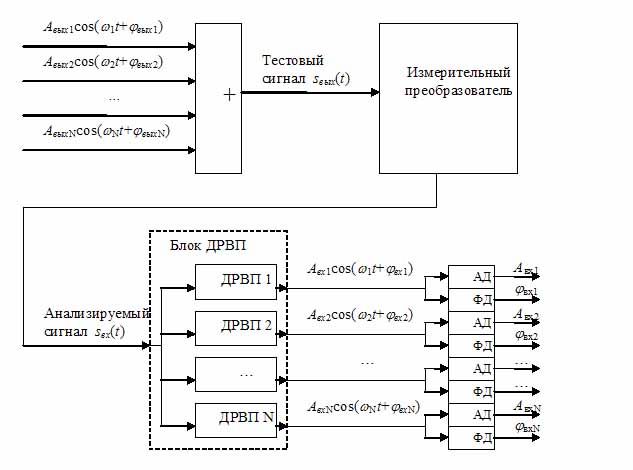
Рисунок 2.

Метод определения спектра на основе ДРВП.

Для измерения амплитудной и фазовой составляющих спектра предложен  метод с использованием дискретных резонаторов второго порядка (ДРВП) [8], изображенный на рисунке 2. Гармонические сигналы, сформированные на входе измерительной системы и характеризующиеся амплитудами (А_вых1, А_вых2, … , А_выхN) и фазами (j_вых1, j_вых2, … , j_выхN), поступают на сумматор и формируют тестовый сигнал s_вых(t). Тестовый сигнал проходит через измерительный преобразователь, на выходе которого регистрируется анализируемый сигнал s_вх(t). В блоке дискретных резонаторов второго порядка каждый резонатор (ДРВП 1, ДРВП 2, … , ДРВП N) настроен на соответствующую частоту одной из гармоник – (w₁, w_2, … , w_N). Блок ДРВП разделяет сигнал на гармоники, каждая из которых поступает на амплитудный детектор (АД) и фазовый детектор (ФД). На выходе АД и ФД регистрируются амплитудные составляющие (А_вх1, А_вх2, … , А_вхN) и фазовые составляющие (j_вх1, j_вх2, … , j_вхN) гармоник. Таким образом, происходит восстановление спектра анализируемого сигнала.

Описанный метод устраняет главный недостаток дискретного преобразования Фурье – жесткую сетку частот. Частоты, которые могут анализироваться этим методом, ограничены только частотой дискретизации, что для исследования областей резонанса пьезоэлементов является чрезвычайно полезным свойством. При этом количество требуемых операций, при прочих равных условиях, оценивается как N², что в сравнении с формулой (10-5) более оптимально, например, для выборки в 1024 элемента – порядка миллиона операций.

Предложенные алгоритмы определения ККПП позволяют значительно повысить эффективность контроля качества пьезоэлементов. Для быстрой оценки ККПП в широком диапазоне частот рекомендуется алгоритм на основе БПФ. Для точной оценки ККПП в узком частотном диапазоне рекомендуется алгоритм на основе набора ДРВП.

Литература.

1.                 Малов В.В. Пьезорезонансные датчики. – 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1989.

2.                 Седалищев В. Н. Высокочувствительные приборы и методы контроля параметров технологических процессов с использованием связанных колебаний в пьезорезонансных структурах: автореф. дис. на соиск. учен. степ. доктора техн. наук. – Барнаул: Изд-во АлтГТУ, 2006.

3.                 Седалищев В.Н. Устройство для измерения уровня сыпучих материалов // Приборы и системы. Управление, контроль, диагностика. – 2006. – №6. – С.49 – 50.

4.                 Зеленка И. Пьезоэлектрические резонаторы на объемных и поверхностных акустических волнах: материалы, технология, конструкция,  применение: пер. с чешск. – М.: Мир, 1990.

5.                 Шермергор Т.Д. Пленочные пьезоэлектрики / Т.Д. Шермергор, Н.Н. Стрельцова. – М.: Радио и связь, 1986.

6.                 Воронов А.С. Теоретическое и экспериментальное исследование амплитудно-частотных и фазочастотных характеристик пьезоэлементов / А.С. Воронов, В.С. Цуриков, С.П. Пронин // Вестник АлтГТУ. – Барнаул, 2006. – № 2. – C. 73-74.

7.                 Воронов А.С. Оптико-электронная измерительная система для определения комплексного коэффициента передачи пьезоэлементов / А.С. Воронов, С.П. Пронин // Приборы и системы. Управление, контроль, диагностика. – 2007. – №3. – С.56–59.

8.                 Сергиенко А.Б. Цифровая обработка сигналов: учебник для вузов. – 2-е изд. – СПб.: Питер, 2006.

Поступила в редакцию 14 августа 2007 г.