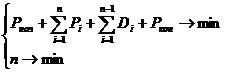Применение цепной резки при фигурном раскрое листовых материалов: описание подхода и алгоритм построения пути.

Тарасенко Павел Юрьевич,

аспирант кафедры Вычислительной математики и кибернетики Уфимского Государственного Авиационного Технического Университета.

При фигурном раскрое листовых материалов часто встречается ситуация, когда толщина раскраиваемого материала слишком велика, чтобы непосредственно начать вырезание. Для обработки таких материалов в определенных точках пути режущего инструмента наносятся специальные отверстия - так называемые точки врезки. Однако при этом расходуется дополнительная энергия и время.

Максимальное количество точек врезки совпадает с количеством контуров на листе. Практически же их число можно значительно уменьшить за счет последовательного ("по цепочке") вырезания двух и более контуров без выключения режущего инструмента (РИ).

1.                              Постановка задачи.

Задача построения пути для цепной резки формулируется следующим образом: необходимо вырезать m контуров так, чтобы количество n точек врезки было наименьшим (n <= m).  

Контуры разделяются на внешние и внутренние. Во внутреннем контуре возможно перемещение без выключения РИ (например - контур отверстия). Взаимные пересечения контуров не допускаются.

Функционально задачу можно разделить на две подзадачи:

1. Построение графа допустимых переходов

Имеется m контуров и информация о вложенности контуров. Необходимо построить ориентированный граф, представленный G = (P,V), где P – контуры, V – разрешенные переходы между ними. Разрешенными будем считать следующие переходы:

·                    переход от контура к непосредственно содержащему его контуру;

·                    пусть k₁ и k₂ непосредственно вложены в один и тот же контур, разрешенным является  переход от контура k₁ к контуру k₂, если k₂ не имеет вложенных контуров, либо от контура k₁ к вложенным контурам контура k₂, не содержащим других вложенных контуров.

2. Поиск пути режущего инструмента с учетом разрешенных переходов, определение точек врезки

Пусть

Задача состоит в нахождении такого пути РИ, чтобы:

            где

2.                              Алгоритм построения пути и определения точек врезки.

Для решения задачи установки точек врезки и поиска пути цепной резки был разработан рекурсивный алгоритм, названный "алгоритмом освобождения контуров".

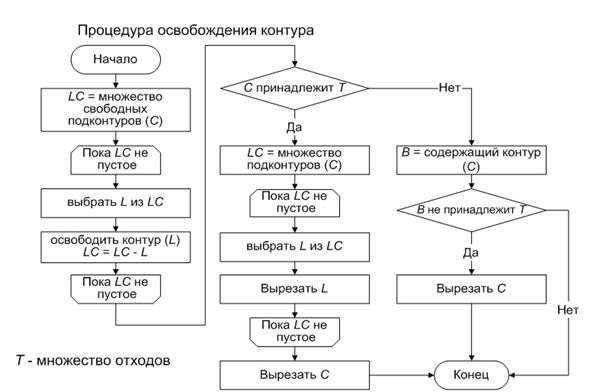
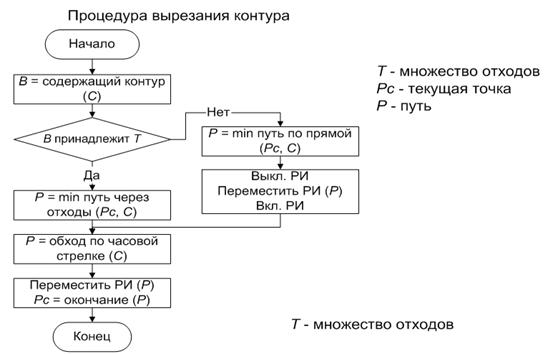
Суть алгоритма в последовательном "освобождении" контуров от вложенных в них контуров.

При этом используются следующие эвристические правила:

1.  Контур считается «свободным», если все вложенные в него контуры вырезаны.

2.  Контур может быть вырезан, если: он свободен и содержащий его контур является внешним, либо, если содержащий контур – внутренний, то вложенные в  него должны быть свободны.

3.                         Заключение.

Предложенный алгоритм автоматического построения пути, не смотря на простоту, позволяет значительно сократить количество врезок на листе за счет фиксации порядка переходов между контурами. При этом возможна дальнейшая минимизация пути режущего инструмента одним из существующих подходов.

4.                         Литература.

1.                SigmaNest Manual, http://www.sigmanest.com. 20 марта 2005 г.

2.                TurboNest Manual, http://www.mtc-europe.co.uk. 15 марта 2005 г.

3.                TurboNest Modules Overview, http://www.mtc-europe.co.uk. 15 марта 2005 г.

4.                D. S. Johnson and L. A. McGeoch, The Traveling Salesman Problem: A Case Study in Local Optimization, Local Search in Combinatorial Optimization, E. H. L. Aarts and J.K. Lenstra (ed), John Wiley and Sons Ltd, 1997, pp 215-310.

Поступила в редакцию 13 ноября 2007 г.