УДК 531+629.5.02.001.24+629.7.02.001.24

Усилия потери устойчивости квадратной двухслойной пластины.

 Аносов Анатолий Петрович,  

доктор технических наук зав. кафедрой Конструкции судов.

Мамонтов Андрей Игоревич,

аспирант кафедры Конструкции судов, заведующий лабораторией.

Дальневосточный Государственный Технический Университет.

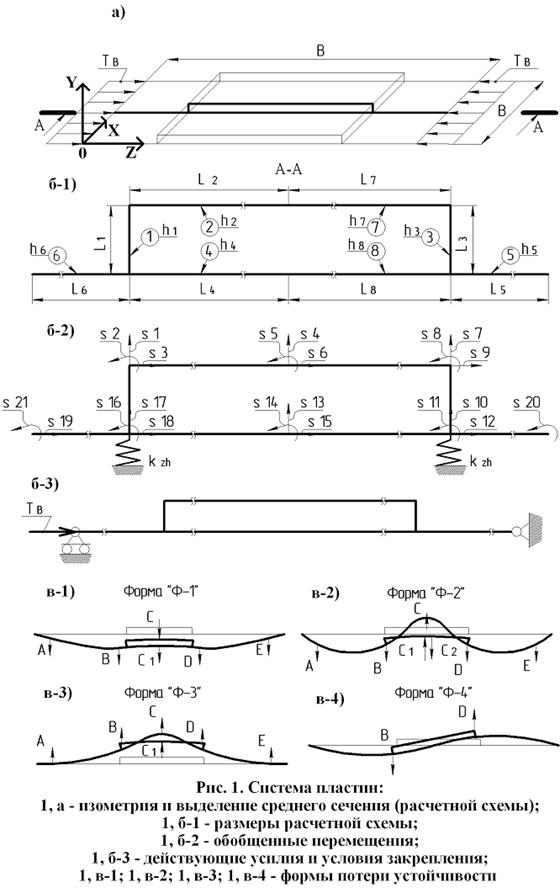
Рассчитывается двухслойная пластина, изображенная на рис. 1, а. Пластина нижнего слоя (нижняя пластина) свободно опирается на жесткий квадратный контур всеми кромками. Пластина верхнего слоя имеет в одном из направлений меньший размер, чем нижняя. В этом направлении она расположена симметрично относительно центра нижней пластины и кромками соединена с ней. Соединение моделируется пластиной с толщиной равной толщине верхней или нижней пластины по принципу «в зависимости от того, что больше». В другом (перпендикулярном) направлении длина верхней пластины равна длине нижней пластины. В этом направлении верхняя пластина имеет опору на контуре, как и нижняя пластина.

Расчетная схема системы пластин образована из среднего сечения А – А и представлена на рис. 1, б. Расчетная схема состоит из нескольких граничных элементов [1, 2], номер каждого из которых выделяется кругом на рис 1, б.

Каждый из элементов на схеме рис. 1, б получен при помощи метода В. З. Власова [3]. При использовании этого метода дифференциальное уравнение сложного изгиба пластины [4] сводится к типу однородного дифференциального уравнения. В рассматриваемой работе указанное преобразование уравнений производится с удержанием  одного члена ряда (первое приближение) в направлении оси OX.

Соединительные элементы 1 и 3 на схеме работают на кручение и, кроме того, являясь ребрами, создают эффект податливых опор. Этот эффект моделируется введением в матрицу всей расчетной схемы коэффициентов жесткости ,

,

где:     -модуль упругости для стали, кГс/мм²;

            -длина ребра или ширина пластины (рис. 1), мм;

            -момент инерции профиля сечения ребра, мм⁴, расчет которого производится с учетом длины присоединенного пояска, равной .

Нижняя пластина сжимается усилиями T _B , приложенными к ее кромке. Сжимающие усилия действуют в направлении перпендикулярном к длинным сторонам верхней пластины (рис. 1, б) и возрастают пошагово. На каждом шаге нагружения применяется итерационный процесс, состоящий из 5 итераций, для определения усилий сжатия в каждом из элементов. Полученные усилия позволяют определить обобщенные перемещения «s» на краях каждого элемента (рис. 1, б), и перемещения внутри, по его длине.

Строятся графики зависимостей перемещений в точках A (точка внутри элемента), B (s 17), С (s 13), C 1 или C 2 (s 4), D (s 10) и E (точка внутри элемента) (рис. 1, в) от T _B, где усилия потери устойчивости T _Э определяются по положению асимптот на графиках этих зависимостей. Форма, по которой система пластин теряет устойчивость, определяется по направлению перемещений в районах асимптот на этих графиках.

Выделяется несколько форм, по одной из которых, в зависимости от варьируемых характеристик, рассматриваемая система пластин теряет устойчивость. Схематично эти формы показаны на рис. 1, в, где стрелками обозначены направления перемещений в области асимптоты.

Для расчета выбираются исходные характеристики расчетной схемы (рис. 1, б): , мм; , мм; , мм; , мм . Величина технологического зазора между пластинами 2 мм : , мм. Значение T _Э откладывается вдоль оси ординат, а соответствующее ему значение длины коротких кромок откладывается вдоль оси абсцисс. Так получается несколько графиков, каждый из которых соответствует определенной толщине пластины верхнего слоя.

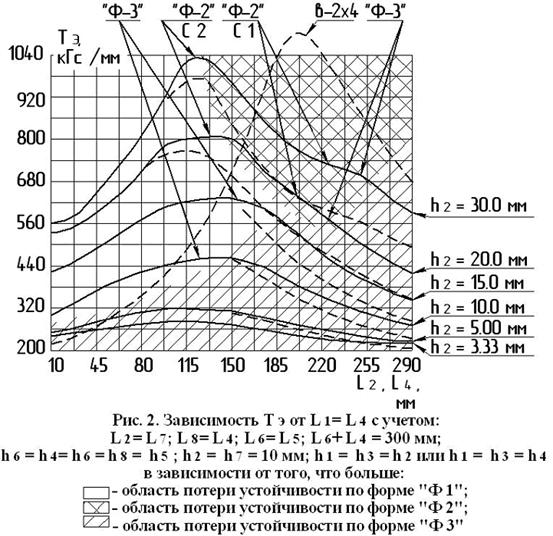
Результат расчета представлен на рис. 2. Стрелками отмечены точки, в которых не действуют формы, указанные на выносках. Стрелки предназначены для определения границ областей, выделенных цветом. До мест, отмеченных стрелками, справа, действуют формы, указанные на выносках.

Жирные штриховые линии на рис. 2 соответствуют значению T _Э , при котором разница перемещений верхней и нижней пластины в вертикальном направлении соответствует 2 мм (величина принятого зазора). Значения этой кривой соответствуют возникновению контакта между поверхностями пластин.

На рис. 2 приведена для качественного сравнения кривая «в-2х4», которая является кривой зависимости значения T _Э от длины накладки с  мм, но без учета влияния краевых эффектов от сторон опорного контура  и . Ее значения вдоль оси ординат умножены на 4.

Сравнивая кривую «в-2х4» и кривую, отмеченную стрелкой с , можно сделать следующие выводы:

Форма «Ф-1» повышает значение T _Э . Это объясняется тем, что при потере устойчивости по этой форме слои в большей степени работают как монолитная пластина (меньше расщепляются). При потере устойчивости по форме «Ф-1» большее влияние оказывает коэффициент жесткости ребер , так как сами ребра оказываются далеко от параллельных им опорных кромок нижней пластины.

Формы потери устойчивости «Ф-2» и «Ф-3» уменьшают значение T _Э по сравнению со значениями кривой «в-2х4». Этот эффект объясняется тем, что, действуя совместно с краевыми эффектами, они приводят к большему расщеплению слоев квадратной пластины, чем пластины сильно вытянутой (сильно вытянутые пластина с накладкой теряют устойчивость по форме «Ф-3», без краевых эффектов).

Наряду с уменьшением T _Э по причинам, указанным в п. 2, значение T _Э для кривых, соответствующих  мм, уменьшается в диапазоне  мм из-за создания благоприятных условий для образования полуволн между ребрами по схеме формы «Ф-2» (рис. 2, в, область темно-серого цвета).

Сопоставление жирных штриховых и сплошных линий показывает, что при малых значениях  верхний слой слабо сопротивляется сжатию. Последнее создает меньший крутящий момент на соединительном элементе, что приводит к уменьшению деформаций центра нижней пластины в вертикальном направлении и к относительному повышению T _Э . Например, в случае  мм верхняя пластина попросту теряет устойчивость, изгибается вверх и не успевает вовлечь в изгиб нижний слой. Контакта между пластинами в этом случае вообще не наблюдается.

Литература.

1.       Баженов В. А. Строительная механика. Применение метода граничных элементов. Специальный курс. / Баженов В. А., Оробей В. Ф., Дащенко А. Ф., Коломиец Л. В. ‑ Одесса: Астропринт, 2001. – 288 c.

2.       Бреббия К. Методы граничных элементов. / Бреббия К., Теллес Ж., Вроубел Л. ‑ М.: Мир, 1987. – 530 с.

3.       Справочник по строительной механике корабля [в трех томах] Т. 2 / под ред. проф. докт. техн. наук О. М. Палий.  - Л.: Изд-во «Судостроение», 1982. – 980 с.

4.       А.А. Курдюмов. Строительная механика корабля и теория упругости. Т. 2. Основы теории упругости. Изгиб и устойчивость пластин и оболочек.  / Курдюмов А.А., Локшин А.З., Иосифов Р.А., Козляков В.В. Л. – Судостроение, 1968. – 464 с.

Поступила в редакцию 12 ноября 2007 г.