Модель декаметрового канала связи с межсимвольной интерференцией.
Богачев Андрей Геннадьевич,
адъюнкт
Академии ФСО России.
Математические модели сигналов в декаметровом
диапазоне волн условно могут быть разделены на
статические и динамические. Так, к основным
статическим моделям относятся одномерные плотности вероятности коэффициентов
передачи радиоканала, отражающие распределения огибающих сигналов и помех, а
также их уровней. Динамические модели описывают временное изменение параметров
сигналов и помех.
При моделировании каналов связи возможны два существенно
разных подхода — структурно-физический и феноменологический [1]. Первый
из них предполагает изучение реальных преобразований переданного сигнала и
механизма образования помех в среде распространения с учетом ее физических
свойств и отражение структуры этих преобразований с необходимой точностью в
модели. К моделям этого типа относится описание линий передачи с помощью
телеграфных уравнений, пространственно-временных радиоканалов – на основе
уравнений Максвелла и т. п.
Феноменологический подход базируется на представлении о канале как о
«черном ящике», внутренняя структура которого не рассматривается, и требует
подбора модели лишь по признаку необходимого приближения наблюдаемых на выходе
сигналов при заданных сигналах на входе. При описании непрерывного канала,
организованного на радиолинии, было бы весьма затруднительно учесть все
реальные преобразования электромагнитного поля в антеннах и свободном
пространстве. Вместо этого такой канал обычно рассматривают как некоторый
фильтр с определенной передаточной функцией или импульсной переходной характеристикой,
т. е. прибегают к феноменологической модели.
Итак, сделаем выводы о пригодности структурно-физических и феноменологических
моделей каналов связи для задач анализа и синтеза систем передачи информации
(СПИ).
1. Структурно-физические модели [2-4].
Весьма сложны, имеют высокую сложность аналитического описания
для которого применяются нелинейные дифференциальные уравнения в частных
производных высокого порядка. Это происходит вследствие попытки учесть большое
количество факторов, влияющих на передачу электромагнитной энергии по каналам.
2. Феноменологические модели [5, 6].
счетчик электроэнергии. Отличные цены. В наличии arzge.ru
Достаточно точно отражают свойства канала связи с одной стороны, и позволяют эффективно решать задачи анализа и синтеза СПИ с
другой.
Феноменологические модели можно классифицировать по способу описания зависимости
выхода от входа.
Прямое описание аналитически задает характер взаимодействия сигнала с
системой и позволяет решить задачу анализа. Однако с его помощью решение задачи
синтеза системы передачи информации является весьма затруднительным.
Косвенное описание модели канала содержит вероятностное
отображение выхода при заданном входе и является основой для синтеза СПИ.
Однако подробный приведенный анализ существующих моделей при косвенном описании
выявил неполноту учета свойств канала, необходимых для решения задачи синтеза.
Так, например, вероятностное описание сигнала на выходе канала не содержит
параметров, описывающих сам канал, и ограничено узким классом входных сигналов.
Неприемлемым также является статическое вероятностное описание каналов, так как
оно не учитывает их память и динамический характер входных сигналов. Кроме
того, приведенные косвенные описания основаны лишь на описании преобразования нескольких
низших моментов случайных процессов в канале связи. В действительности же при
цифровом способе передачи сигналов такие их моментные описания оказываются
недостаточными, так как не учитывают нелинейные свойства входного сигнала.
Анализ последних публикаций в периодических изданиях позволил
выявил тенденцию моделирования канала связи в виде аналитических моделей
импульсной характеристики (ИХ) [7-9]. Однако при цифровой передаче информации
необходимо рассмотрение расширенного канала связи путем включения в него этапов
дискретизации и квантования. Тогда модель импульсной характеристики будет
являться составной частью разрабатываемой модели.
Таким образом, будем формировать модель канала с межсимвольной интерференцией
(МСИ) с учетом следующих требований:
- разрабатываемая модель должна иметь косвенное описание канала отображающее цифровой вход в виде модулирующей
последовательности в непрерывный выход;
- использовать частные модели ИХ непрерывных каналов связи;
- учитывать операции дискретизации и квантования;
- учитывать свойства модулирующей последовательности;
- учитывать многолучевость распространения
радиоволн;
- иметь простое аналитическое описание межсимвольной интерференции с
целью синтеза систем сигналов и разработки алгоритмов оптимального приема.
Определим событийную модель сигнала на выходе канала с межсимвольной интерференции
для некоторого выделенного момента t. Если МСИ не существует, то в выделенный момент времени
мгновенное значение сигнала (далее – состояние сигнала) на выходе непрерывного
канала будет определяться реакцией от передачи одного из сигналов ансамбля
мощностью K. Этот
механизм можно описать с помощью вероятностной смеси [10, 11] K распределений плотности вероятности
каждого сигнала в отдельности. При учете МСИ с каждой компонентой такой смеси
суммируется определенные сигналы от предшествующих значащих интервалов. В
качестве модулирующей последовательности примем двоичную
однородную марковскую цепь с заданной матрицей
переходных вероятностей и вектором безусловных вероятностей начальных состояний
[10]. Тогда каждая компонента смеси формируется путем суммы
реакций канала в данный момент времени t от сигналов передаваемых в предшествующие и рассматриваемый
значащие интервалы. Число учитываемых предшествующих значащих интервалов
NИ
определяется ИХ канала и матрицей переходных вероятностей марковской
цепи. Вектор безусловных вероятностей на предыдущем шаге определяет вероятность
передачи на предыдущем значащем интервале сигнала из ансамбля K. В момент t сигнал от предыдущего шага может
суммироваться с любым сигналом на рассматриваемом значащем интервале. Номер
этого сигнала будет определяться вектором безусловных вероятностей на
предыдущем шаге и матрицей вероятностей перехода за j шагов, где j- разность между номерами
рассматриваемого и предшествующего значащего интервала. Входом канала является марковская последовательность бесконечной длины.
Характеристическая функция динамики одномерной плотности вероятности
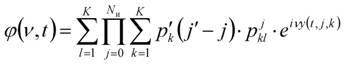
где K- мощность
ансамбля сигналов;
t - текущее
время;
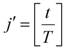-текущее
значение значащего интервала;
T – длительность
значащего интервала;
-реакция
линейной системы в момент t
на k-ый сигнал ансамбля от j-го предшествующего символа символу j/, при этом 
;
NИ-глубина
МСИ в значащих интервалах и памяти источника.
Реакцию линейной системы в момент t на k-ый сигнал ансамбля от j-го предшествующего символа символу j/ найдем по формуле
,
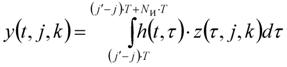где 
-k-ый
сигнал на выходе модулятора для j-го
значащего интервала как функция времени;
- импульсная характеристика канала.
Достоинствами модели являются:
- использование косвенного описания;
- учет памяти источника;
- учет операций дискретизации и квантования;
- возможность использования частных моделей импульсной
характеристики 
любых линейных непрерывных каналов связи.
Общность разработанной модели позволяет конкретизировать ее для частного
случая – декаметрового канала связи с межсимвольной
интерференцией. Тогда в разработанной модели необходимо использовать ИХ декаметрового канала. Для этого можно применить марковскую модель декаметрового
канала связи [7], которая обладает некоторой общностью.
Таким образом, предлагается модель декаметрового
канала связи с МСИ, основанная на рандомизированной
(вероятностной) смеси композиций сигналов от различных элементов модулирующей
последовательности и использовании марковской модели
ИХ канала.
Литература.
1. Кловский Д. Д., Конторович В. Я., Широков С.
М. Модели непрерывных каналов связи на основе стохастических дифференциальных
уравнений / Под ред. Д. Д. Кловского.
– М.: Радио и связь, 1984. - 248 с.
2. Барабашов, Б. Г. Динамическая адаптивная
модель связного декаметрового канала / Б. Г. Барабашов, Г. Г. Вертоградов // Радиотехника. – 1995. – №
12. – С. 29-32.
3. Вертоградов, Г. Г., Уменьшение влияния многолучевости
на точность определения углов прихода интерферометрическими методами / Г. Г.
Вертоградов, Е. В. Кондаков // Радиотехника. – 2003. – № 1. – С. 86-90.
4. Ковалев, И. П. Нелучевая статистическая
модель двухмерного многолучевого радиоканала / И. П. Ковалев // Радиотехника. –
2004. – № 10. – С. 28-32.
5. Семисошенко М. А. Управление
автоматизированными сетями декаметровой связи в
условиях сложной радиоэлектронной обстановки. СПб.: ВАС, 1997. – 364 с.
6. Кловский Д. Д. Передача дискретных сообщений
по радиоканалам. М.: Радио и связь, 1982. – 304 с.
7. Ершов, Л. А. Марковская модель декаметрового
канала связи / Л. А. Ершов, А. В. Коренной, М. А. Шелковников
// Радиотехника. – 1998. – №3. –, С. 57-60.
8. Коренной, А. В. Квазиоптимальный алгоритм фильт-рации импульсной характеристики
декаметрового канала связи / А. В. Коренной, М. А. Шелковников // Радиотехника. – 1998. – № 3. – С. 61-64.
9. Коренной, А. В. Алгоритм квазиоптимальной
фильтрации марковских последовательностей в многолучевых
каналах связи / А. В. Коренной, М. А. Шелковников, Е.
А. Богословский // Радиотехника. – 2003. – № 1. – С. 54-58.
10. Вентцель Е. С. Теория вероятностей: Учеб. для вузов. – 5-е изд. стер. – М.:
Высш. шк., 1998. – 576 с.
11. Тихомиров Д. Л. Эффективность связи и неинформационные параметры сигналов.
М., «Связь», 1975.
Поступила в редакцию 7 августа 2007 г.