Интерполяция установившихся и переходных электрических величин в ЭЭС

 

Гэ Цюнь,

аспирантка.

Научный руководитель – кандидат технических наук, доцент

Арцишевский Ян Леонардович.

Московский энергетический институт (Технический университет).

 

При анализе и проведении исследований установившихся и переходных электрических величин в электроэнергетических системах (ЭЭС) используют следующие способы:

— теоретические аналитические расчеты с использованием различных математических методов, в частности на основе комплексных, символических методов [1] по интервалам времени с постоянными параметрами и конфигурацией расчетной схемы с выдачей результатов расчетов в форме расчетных выражений и цифровых значений электрических величин;

— теоретическое математическое и физическое моделирование по заданным параметрам конфигурации моделируемого объекта с выдачей результатов в форме осциллограмм и их цифровых значений. Для сопоставления с результатами аналитических методов требуется нахождение интерполирующего аналитического представление в виде расчетного выражения;

— практические эксперименты в участке реальной ЭЭС с получением результатов в форме цифровых осциллограмм с помощью цифровых терминалов релейной защиты и автоматики и цифровых регистраторов. Найденные по цифровым осциллограммам интерполирующие расчетные выражения по интервалам сопоставляют с аналитическими формулами.

В перечисленных случаях электрическая величина, например, ток i(t) может быть представлена по интервалам аналитически в виде мнимой части суммы n функций комплексных переменных [2]:

i(t) = Im{exp[t( + jw_k)]},                                                                      (1)

где  = I_mk Ða_k ¾ комплексная амплитуда k-ой слагающей;  + jw_k =  = s_k Ðj_sk ¾ комплексная частота k-ой слагающей [3].

В последних двух случаях по данным в форме цифровых осциллограмм необходимо найти значения параметров каждой составляющей в выражении (1). Целью данной работы является разработка алгоритма определения основных показателей итерационного процесса нахождения значений параметров каждой составляющей интерполяционного аналитического расчетного выражения для представления установившихся и переходных электрических величин в ЭЭС.

Задан интервал времени, т.е. сегмент цифровой осциллограммы тока или напряжения. На этом сегменте имеются две составляющие: синусоида с промышленной частотой (50 Гц) и экспонента. Аналитическая формула в дискретной форме, например, для тока представляется

i(n) = i_s(n) + i_a(n),                                                                                                     (2)

где

i_s(n) = I_m sin(w₀n·T_д+ j),                                                                                          (3)

i_a(n) = A_a exp(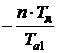).                                                                                          (4)

I_m, w₀ и j ¾ амплитуда, угловая частота и начальная фаза синусоиды;

A_a, Т_a ¾ начальная амплитуда и постоянная времени экспоненты;

f_д и Т_д — частота и период дискретизации цифровой осциллограммы тока.

Известны только дискретные значения суммы в моменты дискретизации. Частота дискретизации выбрана f_д = 600 Гц (период дискретизации Т_д = 1/600 с), т.е. на периоде промышленной частоты (50 Гц) длительностью 20 мс наблюдается N₀ = 12 моментов.

В задаче требуется определить способ организации итерационного этапа нахождения интерполирующего выражения в той же форме записи на одном периоде (20 мс), т.е. определить I_m, j, A_a и T_a. Среднеквадратическое отклонение исходного процесса i(n) и найденного аппроксимирующего процесса i¢(n) на заданном периоде рассчитывается по выражению:

d(%) = 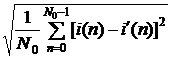· 100 % < 1 %,                                                   (5)

при этом максимальное отклонение, т.е. так называемая в области электроэнергетики полная погрешность [4] определяется по выражению:

e_m(%) = 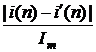· 100 % < 1 %.                                                        (6)

Рассмотрим электрическую величину — ток, являющийся суммой двух составляющих — синусоиды и экспоненты:

i(t) = i_s(t) + i_a(t),                                                                                                        (7)

где четыре параметра (I_m, j, A_a и T_a) полностью определяют значения синусоидальной и экспонентной составляющих этого тока по выражениям:

i_s(t) = I_m sin(w₀t + j),                                                                                                (8)

i_a(t) = A_a exp().                                                                                                (9)

Если периодическая составляющая тока не синусоидальна, то она разлагается на сумму гармонических синусоидальных составляющих.

Как известно, анализ электрических величин сложной формы часто удобнее выполнить, разложив исходную функцию на гармонические составляющие при использовании Фурье анализа [5]. Так как при ограниченном числе членов ряд Фурье обеспечивает наилучшее в смысле среднеквадратической погрешности приближение к исходному сигналу, а при увеличении числа членов ряда Фурье до бесконечности среднеквадратическая погрешность разложения стремится к нулю.

В тригонометрической форме ряд Фурье тока имеет вид

i(t) =  + coskw₀t + sinkw₀t,                                                              (10)

где k = 1, 2, 3, ... — номер гармоники.

Весовые коэффициенты при гармониках a₀, a₁, b₁, …, a_k, b_k, …, можно найти по следующим формулам:

a₀ = dt, a_k = coskw₀tdt, b_k = sinkw₀tdt.                   (11)

Через весовые коэффициенты ряда Фурье определяются:

— уровень постоянной составляющей в токе

A₀ = ,                                                                                                                  (12)

— амплитуда любой гармоники

A_k =,                                                                                                        (13)

— и ее начальная фаза

tg(j_k) = .                                                                                                             (14)

Видно, что при реализации Фурье анализа тока i(t) из-за существования в нем экспоненты появляется уровень постоянной составляющей [5]:

A₀(t) =  = (t) dt = i_s(t) + i_a(t)] dt =

= I_m sin(w₀t + j) + A_a exp()] dt.                                                          (15)

Поскольку

I_m sin(w₀t + j)] dt = 0,                                                                                       (16)

то

A₀(t) = A_a exp()] dt =

= ·[1 - exp(-)]·exp() = A_0m·exp().                                         (17)

Сравнивая (17) с (9), видно,

A₀(t) = K× i_a(t),                                                                                               (18)

и

A_0m = K · A_a,                                                                                                             (19)

где A_0m — начальная амплитуда экспоненты (17);

K = ·[1 - exp()].                                                                                        (20)

Из выражений (19) и (20) видно, что если значения параметров A_0m и K известен, то по (19) можно найти значения параметров экспоненты (Т_a и A_a), и далее найти значения параметров синусоиды (j и I_m).

Зависимость K от постоянной времени Т_a приведена на рис. 1. Значение K при постоянная времени Т_a > 0 находится в диапазоне (0,1).

 

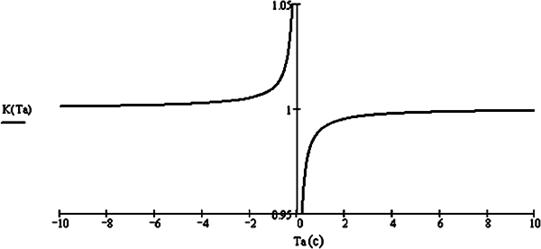
Рис. 1. Зависимость K от постоянной времени Т_a.

 

В области электроэнергетики рассматривается только случай Т_a > 0, и зависимость при этом K от Т_a (0 < Т_a £ 0,2) показана на рис. 2. Для нахождения значения параметров Т_a и A_a зависимость K от Т_a должна быть заранее подготовлена в форме таблицы (см. табл. 1).

 

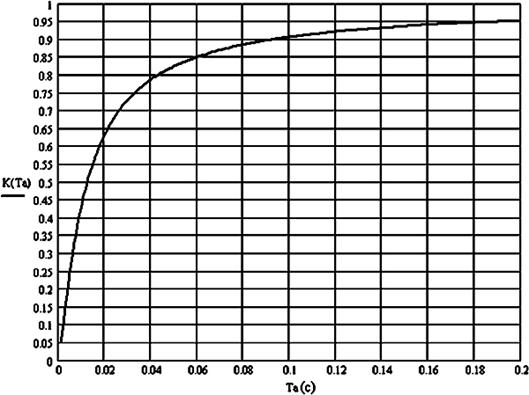
Рис. 2. Зависимость K от постоянной времени Т_a при 0 < Т_a £ 0,2.

 

Таблица 1.

Справочные значения K и Т_a.

K	0,05	0,06	0,07	0,08	0,09	0,10	0,11	0,12	0,13	0,14
Тa(мс)	1	1,20002	1,40004	1,60006	1,80008	2,0001	2,200843	2,401586	2,602329	2,803071
K	0,15	0,16	0,17	0,18	0,19	0,20	0,21	0,22	0,23	0,24
Тa(мс)	3,00389	3,20864	3,413391	3,618141	3,822891	4,028865	4,242677	4,456489	4,670301	4,876481
K	0,25	0,26	0,27	0,28	0,29	0,30	0,31	0,32	0,33	0,34
Тa(мс)	5,104376	5,33227	5,560164	5,770936	6,017241	6,263547	6,509852	6,756158	7,002683	7,270995
K	0,35	0,36	0,37	0,38	0,39	0,40	0,41	0,42	0,43	0,44
Тa(мс)	7,539308	7,80762	8,083089	8,376688	8,670288	8,963887	9,281994	9,603537	9,92508	10,27
K	0,45	0,46	0,47	0,48	0,49	0,50	0,51	0,52	0,53	0,54
Тa(мс)	10,622	10,975	11,358	11,743	12,14	12,561	12,981	13,439	13,897	14,387
K	0,55	0,56	0,57	0,58	0,59	0,60	0,61	0,62	0,63	0,64
Тa(мс)	14,885	15,416	15,957	16,538	17,133	17,765	18,427	19,115	19,845	20,617
K	0,65	0,66	0,67	0,68	0,69	0,70	0,71	0,72	0,73	0,74
Тa(мс)	21,428	22,284	23,191	24,154	25,179	26,272	27,439	28,685	30,018	31,464
K	0,75	0,76	0,77	0,78	0,79	0,80	0,81	0,82	0,83	0,84
Тa(мс)	33,012	34,698	36,525	38,516	40,692	43,084	45,733	48,671	51,888	55,642
K	0,85	0,86	0,87	0,88	0,89	0,90	0,91	0,92	0,93	0,94
Тa(мс)	59,819	64,597	70,102	76,528	84,117	93,22	104,346	118,238	136,104	159,944
K	0,95	0,96	0,97	0,98	0,99
Тa(мс)	193,28	243,312	326,667	493,25	993

           

Для исследования погрешности d от K из рис. 2 выбран ряд точек. На каждой точке — это пара значений K и Т_a. При заданных K и Т_a по (19) можно найти расчетные значения Т_aр и A_aр, что и по (9) можно найти предварительную форму составляющей экспоненты i_aр(t). Из исходного тока компенсируется -i_aр(t), и получается разность i¢_s(t) = i(t) -i_aр(t). Используется Фурье анализ i¢_s(t), и можно найти расчетные значения j_р и I_mр, что и по (8) найти предварительную форму составляющей синусоиды i_sр(t). Так, по (7) сумма i_р(t) = i_sр(t) + i_aр(t) — это найденная аппроксимирующая форма (интерполяция) [6]. По (5) можно найти погрешности d, причем она является зависимостью от K, иными словами, зависимостью от значений Т_a.

Как известно, начальное значение экспоненты зависит от фазы тока в момент возникновения КЗ. Так, для практического исследования погрешности d от значений A_a и T_a выбраны варианты набора начальной фазы (j) тока и постоянной времени (T_a) экспоненты, приведенных в табл. 2.

Для определения первого приближения итерационного значения начальной амплитуды A_0m используется оценка

A_0m = .

 

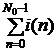Таблица 2.

Варианты набора j, T_a и значения A_a, I_m.

Ta(с) j (°)			1	2	3	4	5	6
			0,006	0,01	0,02	0,03	0,06	0,2
0	0	Aa	0	0	0	0	0	0
		Im	5	5	5	5	5	5
1	30	Aa	-2	-2	-2	-2	-2	-2
		Im	5	5	5	5	5	5
2	60	Aa	-3,4641	-3,4641	-3,4641	-3,4641	-3,4641	-3,4641
		Im	5	5	5	5	5	5
3	90	Aa	-4	-4	-4	-4	-4	-4
		Im	5	5	5	5	5	5
4	120	Aa	-3,4641	-3,4641	-3,4641	-3,4641	-3,4641	-3,4641
		Im	5	5	5	5	5	5
5	150	Aa	-2	-2	-2	-2	-2	-2
		Im	5	5	5	5	5	5

               

Поскольку значение K находится в диапазоне (0,1), то для расчета погрешности d выбрано 95 точек: K = 0,05, 0,06, ..., 0,98, 0,99.Например, в случае K₁ = 0,05, по зависимости K от Т_a (рис. 2 или табл. 1) можно найти соответственное значение Т_aр1 = 0,001. Расчетное начальное значение экспоненты получается по формуле (19):

A_aр1 = .

По расчетным значениям Т_aр1 и A_aр1 аппроксимируют дискретную форму экспоненты по формуле (4)

i_aр1(n) = A_aр1 exp().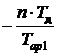

Компенсируя исходные дискретные значения тока расчетными значениями - i_aр1(n), получаются дискретные значения     i¢_sр1(n) = i(n) - i_aр1(n). Расчетные значения параметров I_mр1 и j_р1 получаются по дискретному преобразованию Фурье (ДПФ):

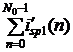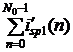a₁₁ = cos, b₁₁ = sin, 

I_mр1 = , j_р1 = arctg().

По расчетным значениям I_mр1 и j_р1 аппроксимируют расчетную дискретную форму синусоиды по формуле (3) i_sр1(n) = I_mр1 sin(w₀n·T_д+ j_р1).

Так, аппроксимируемая дискретная форма тока i₁(n) получается по формуле (1) на основе полученных расчетных значений A_aр1, Т_aр1, I_mр1 и j_р1:

i₁(n) = i_sр1(n) + i_aр1(n).

При этом среднеквадратическое отклонение исходных дискретных значений тока i(n) и найденных дискретных значений i₁(n):

d₁ (%) = 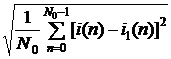 · 100 %.

Далее при K = 0,06, 0,07, ..., 0,98, 0,99 делаем расчет и получаем значения d₂, d₃, ..., d₉₄, d₉₅. Например, ток в случае варианта 21(Т_a = 0,006 с, j = 60°) в табл. 1 показан на рис. 3. По вышеуказанному методу проводится расчет погрешности d при K = 0,05, 0,06, ..., 0,98, 0,99 и получаются значения d₁, d₂, ..., d₉₄, d₉₅. Результат расчета приведен на рис. 3. Таким образом, погрешности d при вариантах 21, 22, 23, 24, 25 и 26 приведены на рис. 3 - 8 (из-за объема статьи здесь показано только эти 6 вариантов).

Когда заданная начальная фаза j = 0, расчетное A_a » 0, поэтому погрешность d не зависит от K, и здесь эти варианты не рассматриваются.

 

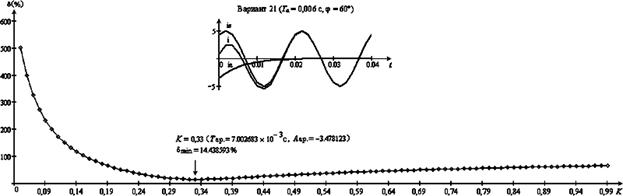
Рис. 3. Погрешность d в случае Т_a = 0,006 с, j = 60° (вариант 21).

 

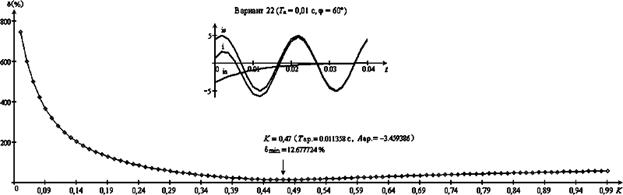
Рис. 4. Погрешность d в случае Т_a = 0,01 с, j = 60° (вариант 22).

 

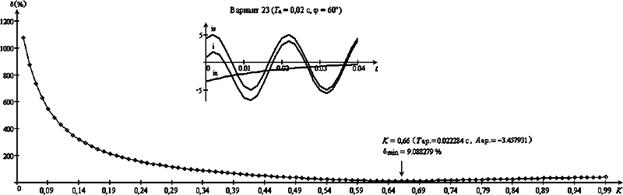
Рис. 5. Погрешность d в случае Т_a = 0,02 с, j = 60° (вариант 23).

 

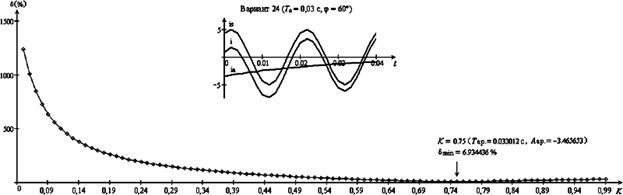
Рис. 6. Погрешность d в случае Т_a = 0,03 с, j = 60° (вариант 24).

 

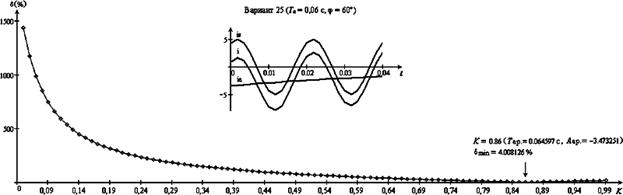
Рис. 7. Погрешность d в случае Т_a = 0,06 с, j = 60° (вариант 25).

 

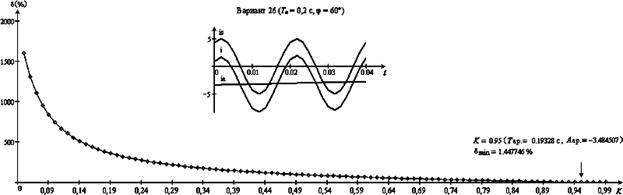
Рис. 8. Погрешность d в случае Т_a = 0,2 с, j = 60° (вариант 26).

 

Из приведенных рисунков и расчета видно, что во всех случаях (варианты набора j и T_a) при расчетных значениях T_aр и A_aр существует только один минимум d_min. Значения среднеквадратической d_min и полной погрешности e_m при расчетных значениях параметров T_aр, A_aр, j_р и I_mр приведены в табл. 3.

 

Таблица 3.

Значения погрешностей d_min и e_m (1-й этап).

Ta(с) j (°)			1	2	3	4	5	6
			0,006	0,01	0,02	0,03	0,06	0,2
1	30	dmin(%)	8,33613	7,319491	5,247123	4,003601	2,314094	0,835857
		em(%)	1,96	2,047	1,906	1,51	0,8468	0,2217
2	60	dmin(%)	14,438593	12,677724	9,088279	6,934436	4,008126	1,447746
		em(%)	3,416	3,566	3,313	2,621	1,468	0,3839
3	90	dmin(%)	16,672259	14,638982	10,494245	8,071925	4,628188	1,671714
		em(%)	3,971	4,122	3,816	2,039	1,693	0,4434
4	120	dmin(%)	14,438593	12,677724	9,088279	6,934436	4,008126	1,447746
		em(%)	3,44	3,552	3,286	2,604	1,463	0,3842
5	150	dmin(%)	8,33613	7,319491	5,247123	4,003601	2,314094	0,835857
		em(%)	1,974	2,039	1,891	1,5	0,8438	0,2218

           

Из результатов расчета в табл. 3 видно, что погрешности вариантов 16 и 56 в первом расчетном этапе уже находятся в диапазоне допустимой (d < 1 % и e_m < 1 %). Это означает, что значения параметров T_aр, A_aр, j_р и I_mр вариантов 16 и 56 могут быть найдены в первом расчетном этапе.

Для понижения погрешности d и получения более точных значений T_aр, A_aр, j_р и I_mр других вариантов необходим дальнейший расчетный этап при использовании метода подбора. Для этого за предварительные значения T_aр, A_aр приняты именно те значения, полученные в первом расчетном этапе.

Кроме вариант 16 и 56, после нахождения расчетных при d_min предварительных значений T_aр, A_aр, j_р и I_mр необходимо найти более точные их значения для того, чтобы d < 1% и e_m < 1%. На основе полученных в первом этапе значений T_aр, A_aр, j_р и I_mр возьмем

(1-25%)T_aр, (1-24%)T_aр, ..., (1-1%)T_aр, (1+0%)T_aр, (1+1%)T_aр, ..., (1+24%)T_aр, (1+25%)T_aр;

(1-25%)A_aр, (1-24%)A_aр, ..., (1-1%)A_aр, (1+0%)A_aр, (1+1%)A_aр, ..., (1+24%)A_aр, (1+25%)A_aр.

По вышеуказанному методу делается расчет для каждой комбинации T_aр и A_aр значений j_р, I_mр и при этом погрешности d и e_m. Например, для варианта 21 (T_aр = 7,002683´10^-3с, A_aр = -3,478123) первая комбинация

T_a1 = (1-25%)×7,002683´10^-3с, A_a1 = (1-25%)×(-3,478123).

Рассмотренным методом можно получить значения j₁, I_m1, и значения погрешностей d₁ и e_m1. Для второй комбинации

T_a2 = (1-24%)×7,002683´10^-3с, A_a1 = (1-24%)×(-3,478123)

получается j₂, I_m2, d₂ и e_m2.

Для вариантов (кроме 16 и 56) в табл. 3 набор комбинаций T_aр и A_aр приведена в табл. 4 рассчитываются в случае каждой комбинации минимум d и e_m и при этом T_a, A_a, j и I_m. Результат расчета приведен в табл. 5.

 

Таблица 4.

Набор комбинаций T_aр и A_aр для вариантов (кроме 16 и 56).

Aaр Taр(с)	1-25%	1-24%	......	1-1%	1	1+1%	......	1+24%	1+25%
1-25%
1-24%
......
1-1%
1
1+1%
......
1+24%
1+25%

 

Таблица 5.

Значения погрешностей d_min и e_m (2-й этап).

Ta(с) j (°)			1	2	3	4	5	6
			0,006	0,01	0,02	0,03	0,06	0,2
1	30	dmin(%)	0,257844	0,160617	0,12641	0,12272	0,243591	——
		em(%)	0,09846	0,04836	0,0564	0,02993	0,09151	——
2	60	dmin(%)	0,446599	0,278166	0,218916	0,212509	0,42182	0,508434
		em(%)	0,1704	0,08376	0,09769	0,05184	0,1585	0,3193
3	90	dmin(%)	0,515688	0,321235	0,252762	0,502157	0,487103	0,587089
		em(%)	0,1967	0,09672	0,1128	0,317	0,183	0,3684
4	120	dmin(%)	0,446599	0,278166	0,218916	0,212509	0,42182	0,508434
		em(%)	0,1705	0,08374	0,09765	0,05184	0,1586	0,3188
5	150	dmin(%)	0,257844	0,160617	0,12641	0,12272	0,243591	——
		em(%)	0,09848	0,04835	0,05638	0,02993	0,09157	——

               

Из табл. 5 видно, что в случаях всех вариантов после второго расчетного этапа получились результирующие значения T_a, A_a, j и I_m, удовлетворяющие требованиям d < 1% и e_m < 1%.

Так, результаты расчета в табл. 3 и 5 показывают, что по приведенному в данной работе методу за два расчетных этапа возможно найти интерполяционные значения сегмента электрической величины длительностью один период с двумя составляющими — экспонентой и синусоидой.

 

Обобщая вышеприведенные исследования можно принять следующий  алгоритм интерполяции переходных и установившихся электрических величин, приведенный на рис. 9.

В алгоритме предусматривается следующие преобразование и расчеты:

Ввод необходимых исходных данных.

Ввод исходных данных: значений промышленной частоты  f₀ (или w₀), частоты дискретизации f_д (или периода дискретизации Т_д), зависимости K от Т_a и др. Поскольку K = 0,05, 0,06, ..., 0,98, 0,99, для экономии запоминающего устройства вводятся только значения K от Т_a на этих 95 точках, приведенные в приложении.

Предварительный Фурье анализ и аппроксимация синусоидой.

Ввод цифровых данных осциллограммы длительностью один период, например, значений тока i(n) при n = 0, ..., N₀ (N₀ = f_д/f₀ — это число цифровых данных на одном периоде). Фурье анализ по следующим формулам

A₀ = ,

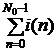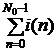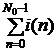a₁ = cos, b₁ = sin.

Так, амплитуда и начальная фаза I_m = , j = arctg().

То ток i(n) можно аппроксимировать i¢(n) = I_m sin(w₀n·T_д+ j).

При этом полная погрешность

e_m(%) = 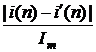· 100 %.

 

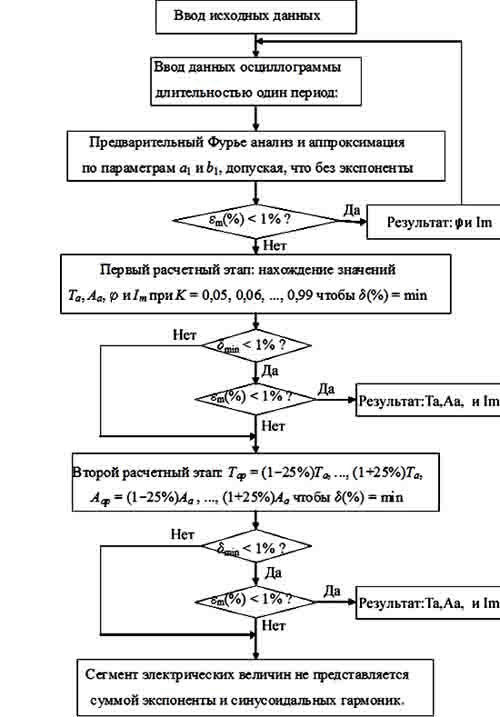
Рис. 9. Блок алгоритма интерполяции электрических величин.

 

Если e_m(%) < 1%, то ток на этом периоде является синусоидальным. Результирующие окончательные значения — это j и I_m.

Первый расчетный этап.

Когда e(%) > 1 %, расчет состоит как максимум из двух этапа. Первым является нахождение значений T_a, A_a, j и I_m при K = 0,05, 0,06, ..., 0,98, 0,99 чтобы среднеквадратическое отклонение

d (%) = 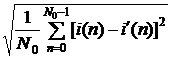· 100 % = min.

При составлении программного обеспечения можно снизить объем расчета, поскольку зависимость d от K при K = 0,05, 0,06, ..., 0,98, 0,99 имеет только один минимум. Поэтому расчет нужно делаться только до d_K(%) < d_K+0,01(%).

Второй расчетный этап.

После нахождения d_min и при этом значений T_a, A_a, j и I_m если d_min < 1%, то проверяется полная погрешность по

e_m(%) = 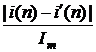· 100 %.

Если e_m(%) < 1%, то параметры T_a, A_a, j и I_m — это окончательные значения, удовлетворяющие допустимому условию e_m(%) < 1%.

Если d_min > 1%, то предусматривается второй расчетный этап. Для экономии объема расчета при каждом выбранном T_a (см. табл. 4) можно делать расчет до d(%) < 1% и e_m(%) < 1%. При этом параметры T_a, A_a, j и I_m — это окончательные значения.

Если за два этапа расчетного процесса не удается подобрать значения параметров апериодической составляющей и гармоник периодической составляющей, то выявляется невозможность представить сегмент осциллограммы в искомой форме суммы экспоненты и синусоидальных гармоник.

Таким образом в работе получен алгоритм и разработаны численные примеры нахождения значений параметров интерполирующего выражения для представления установившихся и переходных электрических величин в участке ЭЭС, причем окончательные значения параметров определяется всего за два расчетных этапа. Если после второго этапа удовлетворяющих условию d(%) < 1% и e_m(%) < 1% параметров не удается определить, то данный сегмент не представляется суммой синусоидальных гармоник и экспоненты, так как в состав электрических величин входят и другие слагающие.

Разработанный алгоритм рекомендуется использовать для сжатия аварийной информации в форме цифровых осциллограмм.

 

Литература.

 

1. Нейман Л. Р., Демирчян К. С., Теоретические основы электротехники: В 2-х т. Учебник для вузов. Том 1. – 3-е изд., перераб. и доп. – Л.: Энергоиздат. Ленингр. отд-ние, 1981. – 536 с.

2. Лосев С. Б., Чернин А. Б., Расчет электромагнитных переходных процессов для релейной защиты на линиях большой протяженности. М., «Энергия», 1972. – 144 с.

3. Арцишевский Я. Л., Гипервекторное представление непериодических несинусоидальных электрических величин, Известия ВУЗов, т. Электромеханика, 1978г., № 8, стр. 817 – 821.

4. Казанский В. Е., Измерительные преобразователи тока в релейной защите. – М.: Энергоатомиздат, 1988. – 240 с.

5. Харди Г. Х., Рогозинский В. В., Ряды Фурье. М., Физматгиз. 1962г., 156 с.

6. Хемминг Р. В., Численные методы (для научных работников и инженеров). М., 1972 г., 400 с.

 

Поступила в редакцию 08.10.2008 г.