Методы определения правильности выборочных ответов.

Хоа Тат Тханг,

аспирант Московского Государственного Строительного Университета.

На сегодняшний день, для определения правильности выборочных ответов, большинство систем дистанционного обучения использует простой анализ выборочного ответа [2]. То есть правильность выборочного ответа оценивается путем сравнения ответа и эталона. Если ответ полностью совпадает с эталоном, то ответ считается правильным. Но если ответ частично отличается от эталона, то ответ считается неправильным и студент при этом не набирает никакого балла. Если учесть, что чаще всего применяется схема "N вариантов – из них один правильный", то такой подход является оправданным. Но в том случае, если применяется схема "N вариантов – из них k правильных (0≤k<N)" или когда требуется установить соответствие, то такой подход не корректен. Следует ввести дифференцированную оценку. Например, ответ (1,3,5) ближе к эталону (3,4,5) чем ответ (2,4,5), поэтому он должен быть оценен выше. Для дифференцирования оценки необходимо использовать подход, который позволял бы определять степень сходства ответа и эталона. Далее рассмотрен подход, предложенный автором.

Схема «N вариантов – из них k правильных (0≤k<N)».

Пусть даны два множества Мэ (множество эталона) и Мо (множество ответа). Элементы двух множеств состоят из пар (х, μ(х))

Где - множество вариантов

или:

Мэ = { ( х_э1, μ(х_э1)), (х_э2, μ(х_э2)),( х_э3, μ(х_э3)),…, (х_э_N, μ(х_э_N)) }

Мо = { ( х_о1, μ(х_о1)), (х_о2, μ(х_о2)),( х_о3, μ(х_о3)),…, (х_о_N, μ(х_о_N)) }

Пусть N = Мах( | Мэ |, | Мо |) = максимальная мощность множеств = количество элементов в множестве.

Пусть

Мк = Мэ ∩ Мо

К = |Мк|

Тогда, если примем r за расстояние между множествами (0 <= r <=1), то

r =1- К/N

Степенью сходства множеств – величина обратная к величине расстояния

δ = 1 – r = К/N.

Таким образом, если вопрос имеет оценку = с, то оценка, получаемая студентом =

Недостаток этого метода в том, что – если в задании «N вариантов – из них k правильных» студент не отмечает ни один верный вариант, то он все равно получает оценку = с*(N-k)/N. Если число верных вариантов близко к N, то такой вариант приемлемый. Но в противном случае, целесообразно применить другой метод.

Пусть даны два множества Мэ (множество эталона) и Мо (множество ответа). (Здесь учитываются только отмеченные варианты)

Где - множество вариантов

или:

Мэ = { х_э1,х_э2, х_э3,…,х_э_M₁ }

Мо = { х_о1,х_о2, х_о3,…,х_о_M₂ }

Пусть N = Мах(|Мэ |, | Мо |) или Мах(М1, М2)

Пусть

Мк = Мэ ∩ Мо

К = |Мк|

Тогда если примем r за расстояние между множествами (0 ≤ r ≤1), то

r =1- К/N

Степенью сходства множеств – величина обратная к величине расстояния

δ = 1 – r = К/N.

Таким образом, если вопрос имеет оценку = с, то оценка, получаемая студентом =

Таким образом, если студент не может выбрать один верный ответ то он не получает ни какую оценку.

Схема «Установление соответствия».

Для ответа студент должен выбрать в левой колонке соответствующий элемент. Для определения расстояния между эталоном и ответом нам легче представлять эталон и ответ как две точки в N арном пространстве. И так:

Хэ = {xэ1, xэ2,…, xэk,…, xэN} – Хэ – эталонный ответ

Хо = {xо1, xо2,…, xоk,…, xоM} - Хо – ответ студента (здесь M <= N)

Коэффициент сравнения определяют следующим образом:

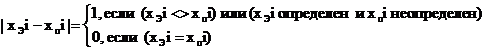
Для определения расстояния между двумя точками воспользуемся обычная формула

Отсюда видно, что наибольшее значение R = N (если все координаты разные или ответ полностью не совпадает с эталоном) а наименьшее значение R = 0 (если все координаты совпадают или ответ полностью совпадает с эталоном)

Если обозначаем 0<=r <=1 то имеем:

Степенью сходства множеств – величина обратная к величине расстояния

δ = 1 – r; .

Таким образом, если вопрос имеет оценку = с, то оценка, получаемая студентом =

Схема «Установление последовательности».

Для списка элементов правильность ответа проверяется путем определения расстояния между списками. Понятие расстояния между списками базируется на работе Кендала [6], где введена мера сравнения порядка списков.

Пусть имеется два списка Хэ, Хо

Хэ = {xэ1, xэ2,…, xэk,…, xэN} – Хэ – эталонный ответ

Хо = {xо1, xо2,…, xоk,…, xоN} - Хо – ответ студента

состоящие из элементов одного и того же базового множества R.

Требуется определить расстояние между списками.

Коэффициент сравнения определяют следующим образом:

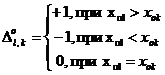
где l<k

Расстояние по Кендалу вычисляется по следующей формуле:

Если компоненты обоих списков упорядочены однотипно, то имеется место следующее равенство: для всех l,k и результат суммирования равен половине числа размещений из n по два. Число размещений из n по два равно:

Поэтому

При этом максимальное расстояние между списками равно 2. Оно получается

в том случае, когда элементы списков упорядочены в противоположном порядке.

Если обозначаем 0<=r <=1 то имеем:

Степенью сходства множеств – величина обратная к величине расстояния

δ = 1 – r; .

Таким образом, если вопрос имеет оценку = с, то оценка, получаемая студентом =

Вопрос в свободной форме.

Задания в свободной форме, бывают в виде арифметического выражения и в виде текстового выражения. В свою очередь, арифметическое выражение может быть вычислимым значением и формулой. По Карпову И.П. [2]. Для вычислимого значения целесообразно определить эталон (правильное значение) и допустимую погрешность ε. Один из вариантов использования погрешности заключается в том, что, если ответ находится в ε-окрестности эталона:

(E – ε) ≤ А ≤ (E + ε)

где Е – эталон, А – полученный ответ, то ответ считается правильным, иначе ответ неверен.

Если выражение требуется рассматривать как формулу, то можно воспользоваться алгоритмом унификации, разработанным в 1966 г. Ж Питра и независимо от него Дж. Робинсоном [5]. Этот алгоритм позволяет определить идентичность любых двух выражений и не зависит от формальной системы, к которой применяется.

Использование ответов, вводимых в свободной текстовой форме, является самой естественной и наиболее сложной задачей при организации системы контроля знаний. Задача распознания текстов на естественном языке была поставлена на рубеже 60х – 70х гг. Были различные попытки ее решения, например [1, 3, 4]. Было создано ряд экспериментальных программ, способных вести диалог с пользователем на естественном языке. Однако широкого распространения такие системы пока не получили – как правило, из-за невысокого качества распознавания фраз, жестких требований к синтаксису “естественного языка”, а также больших затрат машинного времени и ресурсов, необходимых для их работы. Чем длиннее текст, тем сложнее его распознавать.

Для решения этой задачи автор предлагает такой способ:

Необходимо дать обучаемому образец ответа.

· дополнять надо наиболее важное;

· дополняющее слово или словосочетание ставится в конце предложения и лучше должно быть единственным;

Если может быть несколько верных ответов, необходимо их все включить в ответ, чтобы обучаемый выбрав любой верный ответ, получил оценку.

Дополняющее слово или выражение рекомендуется использовать как можно короче.

Если ответ длинный или слишком длинный, в таком случае ответ рекомендуется оценивать только преподавателем.

Для облегчения компьютерного анализа, при сравнении ответа обучаемого и эталона, лучше их все преобразовать в тексты высшего или нижнего регистра. Потом удалить все лишние пробелы, только после этого сравнивать

Литература.

1. Искусственный интеллект : В 3-х кн. Кн. 1. Системы общения и экспертные системы: Справочник / Под ред. Э.В. Попова. – М.: Радио и связь, 1990. – 464 с.

2. Карпова И. П. Исследование и разработка подсистемы контроля знаний в распределительных автоматизированных обучающих системах./ Москва 2002

3. Коутс Р., Влейминк И. Интерфейс "человек-компьютер": Пер. с англ. – М: Мир, 1990. – 501 с.

4. Лехто Г.Ф., Тарасов В.А. Экспертные технологии контроля и диагностики знаний обучаемых // Материалы Международной конференции-выставки "Информационные технологии в непрерывном образовании" // Петрозаводск, 5- 9 июня 1995 г. – http://petrsu.karelia.ru/psu/general/conferences/data/19950605/

5. Лорьер Ж.-Л. Системы искусственного интеллекта. / Пер. с франц. – М.: Мир, 1991. – 568 с. (Алгоритм унификации – с. 116-161.)

6. Фор А. Восприятие и распознавание образов / Пер. с фр. / Под ред. Г.П. Катыса. – М.: Машиностроение, 1989. – 272 с.

Поступила в редакцию 11 февраля 2008 г.