Анализ и решение проблемы удаления узла
из АВЛ-дерева.
Андреев Олег Валерьевич,
доктор химических наук,
профессор,
Филиппов Вадим Анатольевич,
проректор по научной работе,
Лактионов
Федор Викторович,
аспирант,
зав. сектором программного
обеспечения.
Тюменский Государственный
Университет.
Для хранения большого числа упорядоченных информационных
объектов обычно используют двоичные деревья поиска [1, 2, 3]. Сбалансированные
двоичные деревья поиска используют для гарантированно быстрой обработки
информации. АВЛ-деревья – разновидность сбалансированных деревьев, названных по
первым буквам фамилий их изобретателей, Г. М. Адельсона-Вельского и
Е. М. Ландиса (
Цель работы.
Проанализировать результаты балансировки узлов АВЛ-дерева и
выявить причину возникновения ошибок при добавлении и удалении узла из
АВЛ-дерева. Предложить эффективный способ решения проблемы.
Базовая терминология для АВЛ-поворотов.
На рисунке 1 показана ситуация для так называемого правого
поворота, т.е. чтобы восстановить равновесие, нужно перетянуть связку узлов {A, B, C, D, F} вправо, по часовой
стрелке вокруг узла E. В этом случае, узел B встанет на место узла A, а A спустится на уровень узла D. Левое поддерево узла B поднимется на один уровень и тем самым, компенсирует
дисбаланс всего дерева. Узел E после поворота сменит родителя с B на A и устроится в
его левом поддереве.
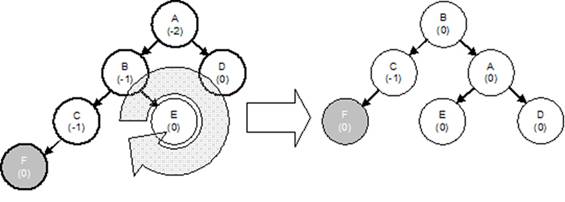
Рис. 1.
Правый поворот в АВЛ-дереве.
Данный фрагмент дерева очень удобен для демонстрации
алгоритма, потому что позволяет построить все возможные варианты
разбалансировки, анализируя балансы только трех ключевых узлов: A, B и E.
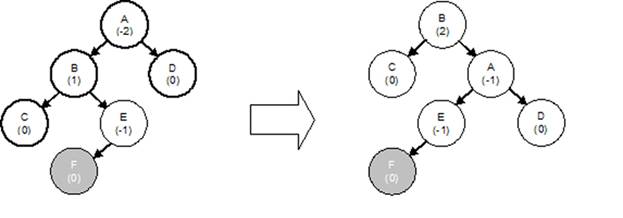
Рис. 2.
Правый поворот в АВЛ-дереве
при добавлении нового узла в поддерево E.
На рисунке 2 видно, что если добавить узел в поддерево E, правый поворот
не изменит ситуации. Дерево останется разбалансированным. В данном случае нужно
повернуть узлы дважды. На рисунке 3 показан двойной правый поворот, который
состоит из левого полуповорота вокруг узла B и правого полуповорота вокруг узла E.
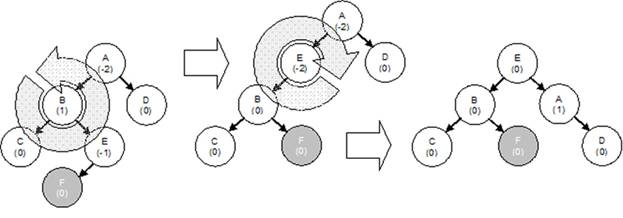
Рис. 3.
Двойной правый поворот в
АВЛ-дереве.
Конечно, нет необходимости последовательно строить оба
полуповорота, достаточно понимать, что узел E проскальзывает между узлами A и B, отдавая при этом им свои соответствующие левое и правое
поддеревья.
Анализ балансировки узлов АВЛ-дерева.
Рассмотрим две таблицы. В первой содержатся значения баланса
узлов A, B и E после двойного правого поворота. Вследствие того, что полуповороты
производились вокруг двух узлов B и E, эта таблица представляет двумерную матрицу переходов для
баланса узлов A, B и E. Как можно заметить, если значение баланса узла B равно -1, то после поворота дерево никогда не
восстанавливает равновесие, а при нулевом
значении баланса узла B существует одна ситуация, когда левое поддерево снова
необходимо перестроить. Таким образом, только при единичном значении баланса узла B можно рассчитывать на лучший результат двойного поворота.
В этом случае, как минимум два узла восстанавливают свой баланс до нуля.
Таблица
1.
Баланс
узлов A,B,E после двойного правого
поворота.
|
B E |
-1 |
0 |
1 |
||||||
|
A |
B |
E |
A |
B |
E |
A |
B |
E |
|
|
-1 |
2 |
-2 |
-1 |
1 |
-1 |
-1 |
1 |
0 |
0 |
|
0 |
1 |
-2 |
-1 |
0 |
-1 |
-1 |
0 |
0 |
0 |
|
1 |
1 |
-3 |
-1 |
0 |
-2 |
-1 |
0 |
-1 |
0 |
Во второй таблице содержатся значения баланса тех же узлов,
но уже после применения простого правого поворота.
Таблица
2.
Баланс
узлов A,B,E после простого правого поворота.
|
B E |
-1 |
0 |
1 |
||||||
|
A |
B |
E |
A |
B |
E |
A |
B |
E |
|
|
-1 |
0 |
0 |
-1 |
-1 |
1 |
-1 |
-1 |
2 |
-1 |
|
0 |
0 |
0 |
0 |
-1 |
1 |
0 |
-1 |
2 |
0 |
|
1 |
0 |
0 |
1 |
-1 |
1 |
1 |
-1 |
2 |
1 |
Здесь следует обратить внимание на то, что баланс узла E всегда остается
неизменным, баланс узла B увеличивается на единицу, а баланс узла A всегда
принимает значение -1, кроме случая
перевеса поддерева B влево.
Теперь можно проследить зависимость между этими двумя
поворотами. По результатам анализа таблиц, во всех ситуациях, решение о
применении того или иного поворота должны основываться на начальном значении
баланса узла B, то есть первого узла относительно разбалансированного, со стороны
которого и произошло нарушение равновесия.
Если баланс этого узла равен -1, то
самый лучший результат даст простой правый поворот. При значении баланса узла B равном единице, лучший результат даст двойной
правый поворот. А при нулевом балансе возникает спорная ситуация, которая
должна решаться самим разработчиком. Хотя двойной поворот и приводит к балансу -2, но, применив второй простой поворот
к его поддереву, большее число узлов будет уравновешено. Это приведет к плавным
изменениям во всем дереве, что в свою очередь обуславливает меньшее число
ситуаций, когда будут необходимы повороты. Тем не менее, намного проще будет
реализовать простой поворот.
Левый и двойной левый повороты строятся аналогично, только
отражены в правое поддерево. Таблицы так же актуальны, только для использования
в левых поворотах, необходимо поменять знаки баланса всех значимых узлов и
значений в таблице.
Условие рекурсивной корректировки АВЛ-узлов.
Если построить все варианты разбалансированного дерева с нулевым балансом узла B и посчитать
высоты деревьев после поворотов, то можно заметить: ни один из этих поворотов
не меняет высоту дерева. Это означает, что баланс дерева, находящегося на
предыдущем уровне необходимо снова скорректировать в зависимости от операции (добавление
или удаление узла), то есть балансировка узлов в данном случае восстанавливает
только локальное равновесие
поддерева, но целевое дерево по-прежнему не сбалансировано. Именно этот момент
является корнем проблем при удалении узла из АВЛ-дерева, поскольку для всех остальных
случаев требуется только один поворот узлов.
Исходя из анализа таблиц балансировки, число поворотов в
худшем случае, когда каждый последующий поворот породит новый, будет составлять
не более log(n) -1, где n
– количество узлов в дереве, при условии, что из всех возможных поворотов,
каждый третий поворот не меняет высоту дерева. В этом случае, вероятность того,
что возникнет второй поворот, составляет 2/3,
так как из трех состояний баланса узла предыдущего уровня {-1,0,+1}, только 0 не
будет выводить дерево из равновесия после коррекции. Но если поворот
потребуется сразу в первом же поддереве верхнего уровня, то, так как узел B будет всегда
иметь баланс, равный по модулю единице,
то независимо от его расположения, следующий двойной поворот всегда будет
приводить дерево в полное равновесие:
{A(t-1)=-1; B(t-1)=1} => { B(t)=1; E(t)=-1}
Таким образом, в операциях добавления и удаления узла,
общее число поворотов составит не более 3*(log2n)/
2. Следовательно, при реализации нерекурсивных методов добавления и
удаления узла, глубина дополнительного стека так же будет составлять не более 3*(log2n)/ 2.
Следует так же заметить, что все остальные повороты всегда
приводят баланс корневого узла поддерева в нулевое состояние. Следовательно,
при добавлении узла в АВЛ-дерево, приращение баланса и соответствующий ему
поворот следует выполнять до тех пор, пока баланс вершины корневого поддерева
не станет равным нулю, а при удалении узла из АВЛ-дерева, наоборот – пока
баланс вершины корневого поддерева равен нулю.
Учет пустого поддерева при реализации
алгоритмов в Visual Studio.
Следует отметить, что, узел B при простом повороте может содержать пустое поддерево (его баланс
может быть неположительным при правом повороте и неотрицательным при левом), а E – его потомок, следовательно,
указатель на узел E может оказаться
недействительным. В Visual Studio версии 6.0, после инициализации переменных
типа Type& производится чтение
её содержимого, что может привести к обращению по нулевому адресу. Чтобы этого
избежать, необходимо использовать в методах переменные типа Type*.
Проверка корректности нерекурсивных методов.
При проведении контрольного тестирования работоспособности
алгоритмов добавления и удаления узлов, для заполнения АВЛ-дерева использовался следующий алгоритм:
1.
Производится обратный обход
некоторой целочисленной последовательности N
= {n0, n1, n2, n3,… nR - 1}: ni = i, где R
– конечное число узлов дерева.
2.
На каждой итерации
обхода, производится случайный выбор индекса k в диапазоне [0…i].
3.
k-й член последовательности N добавляется в
дерево.
4.
Производится обмен
значениями N[k] и N[i], таким образом, имитируется выбывание используемого
элемента из последовательности.
5.
Проверяется дерево на соответствие
критерию АВЛ, в случае несоответствия, счетчик ошибок увеличивается на единицу.
6.
Итерации продолжаются
до тех пор, пока не будут добавлены все R членов последовательности
N.
После добавления всех узлов, число ошибок выводится на
экран.
Удаление узлов дерева производилось по аналогичному
алгоритму, но в качестве исходной последовательности N
использовалась отработанная последовательность, используемая при заполнении
дерева, так как её начальное состояние перед обходом не имеет значения: после заполнения
дерева, индексы последовательности будут только лишний раз перемешаны.
Для того, чтобы убедиться в надежности алгоритмов, тестирование
производилось с R равным 30 000, а число
экспериментов составляло 1000. Системные параметры на исполняем компьютере – Intel® Pentium® 4CPU
2.40 GHz 1,00 Gb ОЗУ Microsoft Windows XP Professional
SP2. На протяжении всех итераций, счетчик ошибок ни разу не
был увеличен, то есть эксперимент полностью подтвердил изначально выдвинутые замечания
по реализации АВЛ-алгоритмов.
Литература.
1.
Кормен, Томас Х.,
Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн, Клиффорд. Алгоритмы:
построение и анализ 2-е издание. Пер. с англ. – М.: «Вильямс», 2005. – 1296 с.
2.
Майкл Ласло.
Вычислительная геометрия и компьютерная графика на C++:
пер с англ. – М.: «Бином», 1997. 304 с.: ил.
3.
Майкл Ласло. Двоичные
деревья поиска:
http://algolist.manual.ru/ds/btree.php
4.
С.Д. Кузнецов, ИСП
РАН, ЦИТ. Методы сортировки и поиска: http://www.citforum.ru/programming/theory/sorting/sorting2.shtml
5.
Балансированные по
весу деревья (АВЛ-деревья):
http://www.mpei.ac.ru/homepages/mm/Lab/A1496/uov/sb.htm
6.
Построение АВЛ-дерева:
http://khpi-iip.mipk.kharkiv.edu/library/datastr/book_sod/kgsu/din_0077.html
7.
AVL-деревья:
http://www.rsdn.ru/article/alg/bintree/avl.xml
8.
Оценки времени
исполнения:
http://www.codenet.ru/progr/alg/sort_search/int.php
9.
Структуры данных и
хэширование:
http://algolist.manual.ru/ds/index.php
Поступила в редакцию 26.03.2008 г.