Автоматический поиск оптимального
пути для подвижного объекта на векторных картах электронно-картографических
навигационных и информационных систем.
Боран-Кешишьян Анастас Леонидович,
аспирант Морской Государственной
Академии имени адмирала
Ф.Ф. Ушакова.
Научный
руководитель: кандидат технических наук, профессор
Сенченко
Виктор Григорьевич.
Сегодня внедрение Электронно-Картографических
Навигационных и Информационных Систем (ЭКНИС) на суда российских судовладельцев
и корабли Военно-Морского Флота РФ, позволяет перейти на качественно
новый уровень организации процессов навигации и управления судном. Штурман,
освобожденный от обработки значительного объема информации, будет иметь
возможность сконцентрироваться на принятии основных стратегических решений, базируясь
на прогнозе и рекомендации автоматических систем, построенных на базе ЭКНИС.
Одна из таких систем может быть представлена в виде программного модуля,
позволяющего автоматически определять безопасную траекторию движения судна на
базе векторной карты, в любой, требуемый ситуацией момент времени.
Нахождение
безопасной траектории следования подвижного объекта, каким может являться торговое
судно или военный корабль,
сводится к проблеме нахождения минимального
по стоимости пути во взвешенном, направленном графе и разрешается применением
алгоритмов, широко используемых
в современной робототехнике. В
качестве таких алгоритмов можно назвать следующие: A-звездочка (А*), Dijkstra, Генетические алгоритмы поиска и другие
[1,2,3,4,5].
Граф строится на базе векторной карты, набор
данных которой может рассматриваться как объектно-ориентированная база данных.
Каждый объект класса
имеет идентификатор объекта, который используется для однозначного определения
данного объекта в системе. Идентификатор назначается системой и не зависит от
состояния объекта.
Курсы кадрового делопроизводства Пройдите курсы 2018 mgutu.ru Изготовление швартовных тумб тсс производство тумб швартовых. Оптимальные цены morskoesoglasie.ru
Так, например объект Wreck на векторной карте стандарта S-57 [6], имеет следующее описание в базе
данных:
Объект: Wreck
Аббревиатура: WRECKS
Код в базе: 159
Тип исходного
геометрического элемента: P, A
Всевозможные атрибуты описываемого объекта
сведены в таблицу 1.
Таблица 1.
Атрибуты объекта векторной карты.
|
Группа атрибутов |
Вид атрибутов |
|
А |
CATWRK; CONRAD; CONVIS;
EXPSOU; NOBJNM; OBJNAM; QUASOUSTATUS; TECSOU; VALSOU; WATLEV; |
|
B |
INFORM; NINFOM; NTXTDS;
PICREP; SCAMIN; TXTDSC; |
|
C |
SORDAT; SORIND; |
Далее более подробно рассмотрим
атрибут CATWRK, который является одним из основных. Последний определяет категорию препятствия
(см. Таблица 2).
Таблица
2.
Категории
атрибута CATWRK.
|
№ |
Значение категории |
INT 1 |
M-4 |
|
1 |
Non-dangerous wreck |
IK 29; |
422.6; |
|
2 |
dangerous wreck |
IK 28; |
422.5; |
|
3 |
distributed remains of
wreck |
IK 31; |
422.8; |
|
4 |
wreck showing mast/masts |
IK 25; |
422.2; |
|
5 |
wreck showing any portion
of hull or superstructure |
IK 24; |
422.2; |
С точки зрения обеспечения
безопасности, наибольший интерес представляет категория dangerous wreck. В данном случае,
при предвычислении траектории движения подвижного
объекта не должны допускаться пересечения ячеек с данным значением категории. К подобным этому, можно отнести
опасные изобаты или запретные для плавания районы.
Для реализации
алгоритмов поиска, карту района необходимо представить
в виде взвешенного графа. Граф в свою очередь трансформируется в весовую матрицу.
Для алгоритмической реализации производим дискретизацию поверхности карты.
Дискретизация – есть процесс разделения карты на равные ячейки, в виде клеток и
более сложных структур. Вся совокупность принятых ячеек и составит граф района [7].
В итоге совокупность
вершин графа представляется в виде сетки, с известными
границами ячеек в географической системе координат ![]()
![]() а так же координатами их центра
а так же координатами их центра ![]() . Размер
ячеек или шаг сетки определяется применительно к конкретному району. Так в
районах с огромным количеством навигационной информации необходимо задаваться
маленьким шагом сетки, чтобы не трансформировать карту в неразрешимую ситуацию.
Необходимо отметить, что при большом шаге сетки в некоторых случаях работы алгоритма построения
траектории может не получиться гладкая линия. Маленький же шаг сетки, в свою
очередь, может замедлить работу алгоритма, но предвычисленная траектория будет
более гладкой и точной в первом приближении.
. Размер
ячеек или шаг сетки определяется применительно к конкретному району. Так в
районах с огромным количеством навигационной информации необходимо задаваться
маленьким шагом сетки, чтобы не трансформировать карту в неразрешимую ситуацию.
Необходимо отметить, что при большом шаге сетки в некоторых случаях работы алгоритма построения
траектории может не получиться гладкая линия. Маленький же шаг сетки, в свою
очередь, может замедлить работу алгоритма, но предвычисленная траектория будет
более гладкой и точной в первом приближении.
Далее необходимо
задаться моделью движения объекта, от чего и будет зависеть сложность дальнейшего
представления района. В нашем случае модель движения усложнена достижением
пункта назначения не только по кратчайшей траектории, но по наиболее
безопасному,
в навигационном отношении, маршруту. Такое усложнение требует
введения понятия стоимости прохождения участка карты.
Процесс переноса
картографической информации с векторной карты на принятую сетку разбивается на
несколько этапов.
Первый этап
заключается в нахождении запретных участков для плавания. К ним причисляем, например,
береговую черту (COALNE), изобаты (DEPCNT) с атрибутом VALDCO, меньшим, чем текущая осадка судна, затонувшее судно
WRECK с категорией CATWRK
- dangerous wreck и
т.д.
Координаты точек ![]() , формирующих запретные
участки и отдельно лежащие опасные объекты, берутся из ООБД векторной карты, затем сравниваются с границами клеток принятой
сетки (
, формирующих запретные
участки и отдельно лежащие опасные объекты, берутся из ООБД векторной карты, затем сравниваются с границами клеток принятой
сетки (![]() ) и
если они попадают в этот диапазон
) и
если они попадают в этот диапазон ![]() , то клетке присваивается
запрет на прохождение (
, то клетке присваивается
запрет на прохождение (![]() ).
).
Второй этап. Рекомендованным
маршрутам (RCRTCL), полосе движения в СРД (TSSLPT) задается вес равный единице.
Третий этап. Всем
ячейкам, заключенным между ¥ и 1, будут присваиваться веса от наибольшего принятого веса до 1.
Так, например, если от препятствия до
опасности заключено 5 ячеек и максимально принятый вес равен 10, то
распределение весов будет происходить следующим образом: ¥ - 10 – 8,2 – 6,4 - 4,6 – 2,8 – 1.
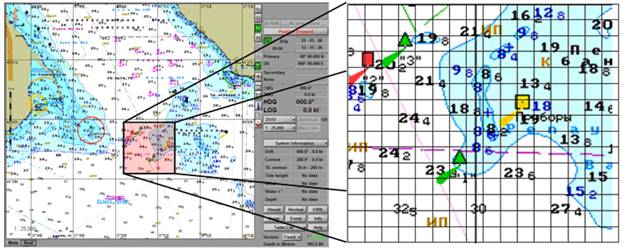
Рис. 1.
Представление векторной карты для реализации алгоритма
поиска траектории.
После производства
трансформации векторной карты, получим матрицу весов (см. Рис. 2), для дальнейшей
реализации алгоритмов поиска пути.
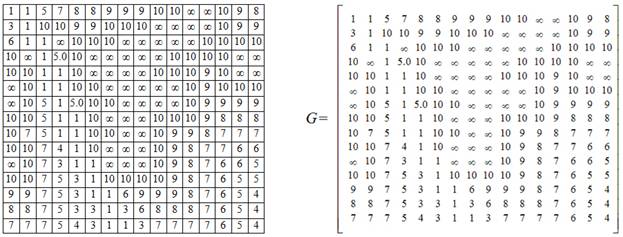
Рис. 2.
Результат трансформации векторной карты в матрицу
весов.
Полученная матрица весов может быть
использована при нахождении траектории с помощью алгоритма Дейкстра
[4], а так же другиx алгоритмов поиска.
Дейкстра разработал классический алгоритм для прохода
по графам, грани которых имеют различный вес. На каждом шаге он ищет
необработанные узлы,
близкие к стартовому, затем просматривает соседей
найденного узла и устанавливает или обновляет их соответствующие расстояния от
старта.
Этот алгоритм принимает во внимание стоимость
или длину пути и обновляет узлы, если к ним найден лучший путь. В нашем случае
наименьшая стоимость прибытия в точку назначения из точки старта, определенная
моделью кратчайшего пути, усложняется стоимостью, зависящей от класса
посещаемой местности. Исходя из этого, полученная траектория будет не только
наикратчайшей, но и оптимальной, проходя, в первую очередь, через наиболее
благоприятные участки карты.
Общая концепция представленная в данной
статье, заключается в разбиении пространства сеткой, которая моделируется
взвешенным графом или матрицей весов, что позволяет решать множество задач связанных
с теорией графов, а так же задачи поиска оптимальной траектории в автоматическом
режиме.
Литература.
1. Cherkassky B. V.,
Goldberg A.V. Shortest Paths Algorithms: Theory and Practice // Technical
Report, STAN-CS-93-1480. Computer Science Department.
2. Kimmel R., Amir A., Bruckstein
A. Finding shortest paths on surfaces using level sets propagation // IEEE
Transactions on Pattern Analysis and Machine Intelligence. vol.
17, no. 6. 1995.
3. Stefanakis E., Kavouras M. On the determination of the Optimum Path in
Space from A.U. Frank, W. Kuhn (editors) Spatial Information Theory // A
theoretical basis for GIS, COSIT95 Proceedings. LNCS 988.
1995.
4. Dijkstra E. W. A note on
two problems in connection with graphs // Numerische Mathematik. 1959.
5. Goldberg, D. E.
Genetic Algorithms in Search, Optimization, and Machine Learning // Addison-Wesley:
6. International
Hydrographic Organization. IHO transfer standard for digital hydrographic data
// Publication S-57. Edition 3.1. 2000.
7. Gibbons. A. Algorithmic Graph Theory // Cambridge University Press Ltd. 1985.
Поступила в редакцию 31.03.2008 г.