Определение
координат быстро движущегося объекта с использованием низкоскоростных
видеокамер.
Кочин Александр Васильевич,
кандидат
физико-математических наук,
Трещалин Андрей Петрович,
соискатель,
ассистент кафедры Радиотехник,.
Московский
Физико-Технический Институт.
1. Введение.
Определение координат объектов
по видеопоследовательности, полученной от нескольких камер видеонаблюдения -
актуальная задача в таких областях, как охранные системы, системы обеспечения
безопасности, диспетчерские системы и т.д. В последнее время все чаще подобные
системы стали применяться для технического обеспечения различных спортивных
соревнований.
В настоящей работе
рассматривается создание прототипа теннисного судьи.
Прототип должен удовлетворять
следующим требованиям:
1. Время срабатывания не более 0.3 сек.
2. Точность определения места касания не хуже 10 см.
Сложность задачи состоит в том,
что скорость полета теннисного мяча может достигать 200 км/ч и более. При
использовании обычных видеокамер с черезстрочной разверткой и частотой кадров
25 кадров/сек. за время кадра мяч пролетит до 3 метров. Это означает, что для
получения требуемой точности необходимо либо использовать высокоскоростные
видеокамеры, либо использовать нестандартные методы видеообработки. Стоимость
высокоскоростных видеокамер оказывается слишком высокой для построения подобных
систем. В данной работе описывается вариант построения системы, использующий
обычные камеры видеонаблюдения.
Основная идея построения
рассматриваемой системы состоит в следующем.
В качестве датчиков используются
видеокамеры с черезстрочной разверткой системы PAL. Частота следования кадров
25 кадров/сек, следовательно частота полукадров получается 50 полукадров/сек.
При этом выдержка устанавливается равной длительности полукадра, т.е. 20
миллисекунд. В результате на последовательности видеокадров после
видеообработки возможно получить практически непрерывное изображение траектории
движения мяча.
Далее предположим, что имеются
две видеокамеры, для которых произведены процедуры калибровки и привязки. Тогда
имеются два двумерных изображения траектории полета мяча, полученные с откалиброванных
и привязанных камер. С другой стороны полная калибровка и привязка камер
означает, что известны фундаментальная матрица и полная матрица преобразований,
связывающие координаты точек изображений и трехмерных мировых координат.
Используя эпиполярную геометрию
и известную фундаментальную матрицу, можно найти на изображении траектории,
полученной со 2-й камеры, точку, соответствующую точке, заданной на изображении
траектории, полученной с 1-й камеры и наоборот.
Далее имея две соответствующие
точки на изображениях, полученных с двух камер, с помощью матрицы
преобразований находим трехмерную мировую координату токи траектории.
В результате получаем трехмерную
траекторию полета мяча. При этом точность получения координат траектории
зависит от разрешения видеокамер, расположения камер, точности калибровки и
привязки.
Был разработан макет системы,
состоящий из
1) двух видеокамер;
2) двух плат видеообработки на основе сигнального процессора;
3) персонального компьютера.
Видеосигнал с каждой камеры
подается на свою плату видеообработки для выделения движущихся объектов и
определения двумерной траектории движения мячика.
Траектории передаются в
компьютер для получения трехмерной траектории и определения координат места
касания мячиком корта.
В настоящей работе описывается
получение двумерных координат изображения траектории полета мяча из
видеопоследовательности, полученной от одной камеры.
2. Описание алгоритма
определения двумерной траектории.
Нахождение двумерной траектории
состоит из следующих основных задач:
1. Выделить точки движущегося объекта.
2. Сформировать прямоугольные объекты.
3. Определить начало траектории в кадре и отслеживать
траекторию после нахождения начала.
4. Получение двумерных координат изображения траектории.
2.1. Определение
движущихся точек.
Определим кадр изображения,
взятый в момент времени 
как множество 
точек (x,y) . Пусть 
– функция яркости
точки изображения, определённая на множестве .
2.1.1. Простейший алгоритм
выделения точек объекта.
Рассмотрим простейший алгоритм
вычитания фона [1].
Алгоритм сохраняет первый кадр видеопоследовательности, а потом для каждого
следующего кадра применяет порог к модулю разности текущего и сохраненного
изображения по каждому пикселю.
1. Сохраняем первое изображение видеопоследовательности.
Обозначим его , а яркость точек как B.
2. Для каждого следующего кадра (обозначим текущий кадр 
, а яркость точек как C) если
, x = 1 … w, y = 1 …
h, где w и h это ширина и высота картинки соответственно, то
пиксель (x,y) считается переднеплановым, иначе он считается заднеплановым.
2.1.2. Алгоритм, основанный на
нормальном распределении.
Рассмотрим алгоритм,
использующий нормальное распределение [1, 2]. Данный алгоритм
моделирует каждый пиксель заднего плана с помощью одномерной нормально
распределенной случайной величины т.е.
Первые n кадров (когда камере
виден только задний план) для каждого пикселя алгоритм производит оценку
параметров модели 
и 
, используя аппарат математической статистики, а после того
как обучение закончено, попиксельно использует вероятностный порог для того,
чтобы определить принадлежит ли значение пикселя заднему плану или переднему.
Итак:
1. Обучение модели заднего плана по первым n кадрам. Для оценки
параметров модели и для каждого пикселя можно применять выборочное среднее и
среднее квадратичное отклонение значений в данном пикселе т.е.
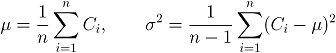
где 
- значения в пикселе
по первым n кадрам.
2. Далее для каждого следующего кадра и для каждого пикселя.
Обозначим C значение в текущем кадре для (x,y) пикселя. Если 
, то данный пиксель сегментируется в задний план, иначе он
сегментируется в передний план.
Параметр e влияет на
чувствительность алгоритма. Очень часто пользуются e=3.
Алгоритм должен обладать
свойством адаптации к изменениям заднего плана, поэтому для среднего значения и отклонения применяется скользящее
среднее.
2.2. Группировка в
прямоугольные объекты.
Прямоугольные объекты
используются для определения появления мяча в поле зрения камеры.
Пусть необходимо выделить
прямоугольные области изображения, охватывающие достаточно крупные движущиеся
объекты [3].
После процедуры выделения
движущихся точек принимают значения 0
для заднего плана и 1 для объекта. Обозначим через 
множество точек 
.
Задачу можно формализовать
следующим образом : необходимо разбить множество точек на максимально
возможное число прямоугольных подмножеств 
так, чтобы они не
пересекались. Введем также обозначение 
для упорядоченного
множества прямоугольных подмножеств .
В терминах теории графов можно
предложить следующий алгоритм решения формализованной задачи :
1. На множестве конструируем графы с
вершинами – точками 
и следующим критерием
связности: точки, лежащие рядом друг с другом – связные.
2. Конструируем графы более высокого уровня с вершинами –
прямоугольниками, охватывающими графы более низкого уровня, и связностями –
ненулевое пересечение этих прямоугольников.
3. Повторяем пункт 2 до тех пор, пока не получим несвязный граф
наивысшего уровня.
Полученные прямоугольные области
как раз и охватывают движущиеся объекты на исходных изображениях. Подмножество описывается
упорядоченной совокупностью чисел 
, где 
– минимальные и
максимальные координаты x и y , выбранные из всех точек 
; nG – число точек 
. Множество 
описывается некоторым
упорядоченным списком подмножеств с указателем на так
называемый граничный элемент списка. Также используется исходная матрица , заполненная
значениями яркости точек 
, принимающими значения 0 и 1.
1. Наращиваем значение y (переходим к элементам
следующей строки матрицы ).
2. Если для граничного подмножества выполняется условие 
, то граничным становится следующий элемент фактор-множества
и повторяется шаг 2.
3. Наращиваем значение x (переходим к элементу
следующего столбца матрицы ).
4. Если 
, то для подмножеств из множества , начиная с граничного
и заканчивая последним, проверяется, не примыкает ли точка (x,y) к текущему
подмножеству по условию:
Если да, то включаем текущую
точку (x,y) в текущее подмножество , производя необходимое изменение координат подмножества, и
увеличивая на единицу счётчик nG.
5. Если на шаге 4 точка (x,y) не была включена ни в одно из
рассмотренных подмножеств , то добавляем новое подмножество вида (x, y, x, y,1) в
конец множества .
6. Переходим к шагу 3, если в строке матрицы остались ещё элементы.
7. Проверяем попарно все граничные подмножества и, если пересекаются,
то объединяем их. При этом условие пересечения двух подмножеств можно записать
в виде : 
или 
и 
или 
.
8. Соответствующим образом изменяя значение y ,
переходим к шагу 1, если ещё не перебрали все строки матрицы .
2.3. Поиск начала и
отслеживание траектории.
Для нахождения траектории полета
мяча необходимо определить начало траектории, то есть понять, что в поле зрения
видеокамеры появился летящий мяч. Очень удобно для этой цели использовать
моменты.
Моменты подмножества G
бинарного изображения определяются следующим образом:
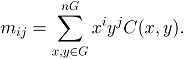
Ориентация главной оси инерции:
Эксцентриситет (удлиненность):
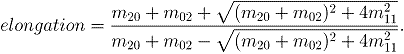
Таким образом, если в двух
полукадрах одного кадра имеются объекты, имеющие близкие ориентации главных
осей инерции и эксцентриситет, расположены как "продолжение" один другого
и с числом точек больше порогового значения, то можно считать, что найдено
начало траектории.
2.4. Получение двумерных
координат изображения траектории.
Для определения точек
траектории, находим "вписанные мячи".
1. Если длина прямоугольного объекта больше высоты, то проходим
по всем X, иначе проходим по всем Y объекта.
2. Для каждого X (соответственно Y) находим 
такие, что расстояние
между соседними точками, определенными ранее как точки объекта, не превышает 2.
Центры этих "вписанных
мячей" и будут искомыми точками траектории.
3. Техническая реализация и результаты экспериментов.
Для экспериментальной проверки
алгоритмов был разработан макет электронного теннисного судьи, состоящий из
- Двух цветных камер видеонаблюдения Sanyo VCC-6572P:
1.
видеовыход системы PAL (720 x 576
точек, 25 кадров в секунду);
2.
черезстрочная развертка
(50 полукадров в секунду);
3.
внешняя синхронизация
(видеосигнал с выхода первой камеры подается на вход синхронизации второй
камеры).
- Двух плат видеообработки ADSP-BF561 EZ-KIT Lite, включающих:
1.
сигнальный процессор ADSP-BF561 Blackfin;
2.
оперативная память 64 MБ (16 M x 16-бит x 2);
3.
флэш память 8 MБ (4 M x 16-бит);
4. видео декодер ADV7183A;
5. последовательный порт.
- Персонального компьютера (ноутбука):
1.
процессор Pentium 1.6 ГГц;
2.
оперативная память 512 МБ;
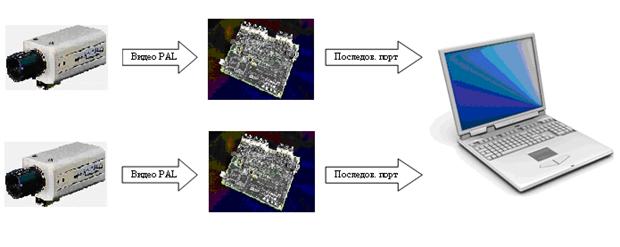
Рис. 1.
Структурная схема прототипа электронного теннисного судьи.
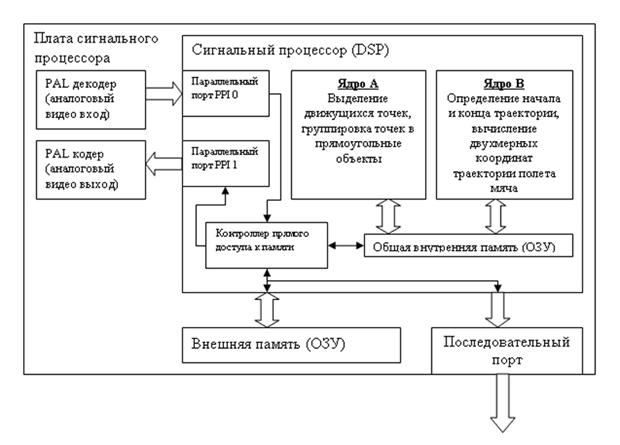
Рис. 2.
Плата сигнального процессора.
3.1. Результаты испытаний.
Точность определения координат
места касания корта мячиком, полученная в результате эксперимента:
Координата Х (поперек корта) <
10 см;
Координата У (вдоль корта) <
3 - 5 см;
Камеры расположены по краям
корта на расстоянии ~ 2 м от корта на высоте ~ 1.5 м, касание в квадрате
подачи, скорость полета мяча ~ 10 - 50 м/с.
4. Выводы.
Предложены алгоритмы,
позволяющие получить двумерные координаты изображения траектории полета мяча из
видеопоследовательности, полученной от "медленной" видеокамеры.
Результаты экспериментов показывают, что при этом возможно достигнуть точности
до одного пикселя матрицы видеокамеры.
Литература.
1. http://cgm.graphicon.ru/content/view/67.
2. Omar Javed,
Khurram Shafique, Mubarak Shah "A Hierarchical Approach to Robust
Background Subtraction using Color and Gradient Information", 2002.
3. http://cgm.graphicon.ru/content/view/53/.
Поступила в редакцию
17.06.2008 г.