Повышение финансовой пропускной способности центра обработки данных

 

Ворожцов Анатолий Сергеевич,

кандидат технических наук, доцент,

Тутова Наталья Владимировна,

аспирант Московского технического университета связи и информатики.

 

В настоящий момент многие операторы связи и сервис-провайдеры оказывают услуги хостинга приложений электронной коммерции в центрах обработки данных (ЦОД). В пиковые периоды нагрузка, поступающая на сайты электронной коммерции, может значительно превышать средние показатели. В результате Web-серверы могут оказаться не в состоянии обслужить всех клиентов. Долгое время ожидания загрузки Web-страниц и отказы в соединении являются типичными индикаторами плохого качества обслуживания на сайтах электронной коммерции. Качество обслуживания снижается для всех пользователей, посещающих сайт в течение пиковых нагрузок, поскольку ресурсы делятся поровну между всеми пользователями. Стандартные политики управления ресурсами серверов ЦОД не различают пользователей и не оказывают дифференцированного качества обслуживания. Поэтому в случае плохого качества обслуживания с сайта могут уйти пользователи, в том числе активно делающие покупки.

Ресурсы в системах электронной коммерции должны выделяться из экономических соображений, учитывая поведение пользователей на сайте. Так, активным пользователям наиболее склонным сделать покупку необходимо предоставить наилучшее качество обслуживания. Поскольку технические ресурсы сайты ограничены, это может достигаться за счет сокращения ресурсов для пассивных пользователей.

Поведение пользователей сайтов электронной коммерциии характеризуется сессией. Под сессией понимается последовательность логичных и связанных запросов и время на обдумывание между запросами от одного пользователя за одно посещение сайта. Время на обдумывание является интервалом времени, начинающимся после ответа системой электронной коммерции на запрос пользователя и до поступления нового запроса в систему от этого пользователя.  Причем время на обдумывание должно быть меньше некоторого порогового значения, при превышении которого считается, что запрос от этого же самого пользователя принадлежит уже другой сессии.

Поведение пользователей на сайтах электронной коммерции рассматривалось в различных работах. Различные типы пользователей характеризуются различными типами сессий. Так пользователи, имевшие длинную сессию, очень редко делали покупки, тогда как пользователи, имевшие сравнительно короткую сессию, делали покупки наиболее часто. Это можно объяснить тем, что пользователи, которые делают покупки, заранее знают, зачем они пришли на сайт, тогда как остальные пользователи просто просматривают описания товаров [1].

В [2] предложена политика управления ресурсами сайта электронной коммерции с целью увеличения финансовой пропускной способности, под которой понимается денежная сумма, накопленная в электронных корзинах покупателей и трансформированная в доход торговой компании. Управление ресурсами было основано на схеме выставления приоритетов пользователям. Приоритеты выставлялись в зависимости от длины сессий, измеряемой числом запросов, и сумме, накопленной в их электронных корзинах. В соответствии с приоритетом пользователям выделяется определенный набор технических ресурсов, таких как процессоры, диски, память. Проведенное имитационное моделирование показало, что в результате использования такой схемы приоритетов финансовая пропускная способность сайта электронной коммерции в периоды пиковых нагрузок может быть увеличена от 5 до 30%.

В работе предлагается альтернативный подход к определению длительности сессии, путем нахождения аналитического выражения плотности вероятности длительности сессий, в соответствии с которым будут приниматься решения о присвоении приоритетов. Нахождение плотности распределения вероятностей длительности сессий традиционным путем обработки статистики является некорректным, поскольку при превышении времени на обдумывание порогового значения сессия автоматически закрывается. Для решения этой проблемы определим плотность распределения вероятности длительности сессий через распределения таких случайных величин, как число поступивших сессий и относительное число элементарных запросов в сессии. Элементарный запрос характеризуется длительностью, которая складывается из минимальной длительности загрузки страницы и минимального времени на обдумывание. Для каждого сайта длительность элементарного запроса может быть различной.

Результаты обработки статистики сайтов электронной коммерции приведены в различных работах. Поступление сессий подчиняется закону Пуассона, а время на обдумывание имеет логарифмически-нормальное распределение [3].

Эти результаты во многом совпадают с результатами обработки журналов доступа Web-серверов российских сайтов электронной коммерции в часы наибольшей нагрузки. Гипотезы о том, что поступление сессий подчиняется закону Пуассона, а число элементарных запросов в сессию, большую часть которого составляет время на обдумывание, распределено по логарифмически-нормальному закону, не противоречат наблюдениям.

Знание этих закономерностей позволяет сделать вывод плотности вероятности длительности сессий. Выражение, связывающее длительность сессии τ_i c относительным числом элементарных запросов x и количеством сессий N за период наблюдений T, можно записать следующим образом:

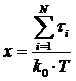,                                                                                                              (1)

где 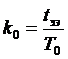 — безразмерный постоянный для данного сайта коэффициент;

t_эз — длительность элементарного запроса;

T₀ — минимальный период наблюдения за реализацией пользовательских сессий;

T — время наблюдения за реализацией пользовательских сессий.

Предположим, что длительности сессий, инициируемых различными пользователями, распределены одинаково и независимо, а также не зависят от общего числа сессий за период T.

Используя принятые допущения, было найдено выражение, связывающее характеристическую функцию относительного числа элементарных запросов φ(t) c характеристической функцией длительности сессии φ₁(t), имеющее следующий вид:

.                                                                                               (2)

Если параметр логарифмически-нормального закона σ ≤ 0,1, то допустима приближенная замена логарифмически-нормального закона распределения числа запросов нормальным [4], характеристическая функция которого имеет вид:

,                                                                                                    (3)

где (a, σ²)—параметры нормального распределения.

Подставив выражение (3) в формулу (2) и прологарифмировав, получим выражение для характеристической функции длительности сессий.

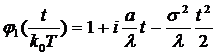                                                                           (4)

Найдем 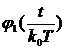 при . Для этого необходимо построить зависимости параметров от времени α(T), σ(T) и λ(T). Данные зависимости хорошо аппроксимируются функциями вида , тогда:

(T) = ;                                                                                      (5)

(T) = ;

(T) = .

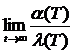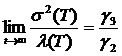Тогда пределы  =  = с₁ и = с₂.

Таким образом,

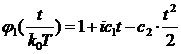.                                                                                   (6)

Полученное выражение характеристической функции длительности сессий позволяет найти плотность распределения вероятности относительной длительности сессий, имеющее следующий вид:

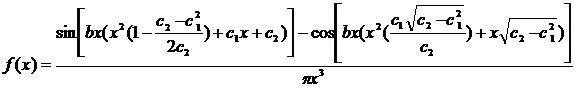, (7)

где .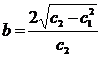                                                                                                        

Поскольку выражение (7) найдено при условии, что параметр закона распределения числа запросов σ ≤ 0,1, то это в значительной степени ограничивает область его применения. Поэтому целесообразно найти такое выражение для распределения длительности сессий, которое было бы справедливо для σ > 0,1. Известно, что закон распределения случайной величины может быть представлен рядом Эджворта, первые члены которого составляют А-ряд Шарлье и имеют вид [5]:

,                                                    (8)

где ;                                                                                                         (9)

x — случайная величина, закон распределения которой аппроксимируется рядом Эджворта;

 — оценка математического ожидания этой случайной величины;

f₂(z), f₃(z)—производные второго и третьего порядка от нормальной плотности вероятности f(z);

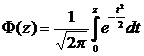;                                                                                            (10)

 — оценка ассиметрии;                                                                            (11)

 — оценка эксцесса;                                                                         (12)

, ,  — оценки второго, третьего и четвертого центральных моментов соответственно.

Таким образом, зная первый начальный момент, второй, третий и четвертые центральные моменты длительности сессий, можно получить приближенное выражение для ее закона распределения.

Известно, что знание закона распределения позволяет определить все его моменты, поэтому можно считать моменты распределения числа запросов и распределения числа сессий известными.

Выразим требуемые моменты распределения длительности сессий через указанные известные моменты (логарифмически-нормального и Пуассона), воспользовавшись полученным соотношением (2).

Отсюда можно получить следующее:

,                                                                                           (13)

где   — характеристическая функция длительности сессий;

 — характеристическая функция числа запросов.

Известно также [6], что начальные моменты распределения определяются через характеристическую функцию. Эта взаимосвязь позволит определить первый, второй, третий и четвертые начальные моменты распределения длительности сессий:

;                                                                                                                  (14)

;                                                                                                   (15)

;                                                                                   (16)

,                                                        (17)

где α₁, α₂, α₃, α₄ — первый, второй, третий, четвертый начальные моменты числа запросов.

Зная начальные моменты, определим центральные моменты распределения длительности сессий.

r₁=0;

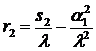,                                                                                                        (18)

где s₂ — второй центральный момент распределения числа запросов;

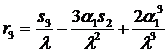,                                                                                      (19)

где s₃—третий центральный момент распределения числа запросов;

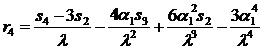,                                                               (20)

где s₄—четвертый центральный момент распределения числа запросов.

Подставляя найденные моменты в формулу закона распределения длительности сессий F(z), представленную первыми четырьмя членами ряда Эджворта, получим выражения для плотности вероятности относительной длительности сессий в виде:

,

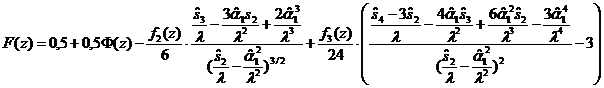где 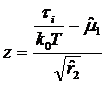;                                                                                               (21)

— относительная длительность i-ой сессии;

— оценка первого начального момента распределения относительной длительности сессий;

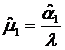 — оценка первого начального момента распределения числа запросов;

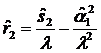— оценка второго центрального момента распределения относительной длительности сессий;

 — оценка второго центрального момента распределения числа запросов.

Аналитическое выражение плотности распределения длительности сессий может использоваться для обоснования выставления приоритетов пользователям сайтов электронной коммерции в политике управления ресурсами серверов ЦОД сервис-провайдера, предложенной в [2]. При этом, в зависимости от параметра закона распределения числа элементарных запросов, для нахождения плотности распределения вероятности длительности сессий может использоваться выражение (7), либо (21).

 

Таким образом, поступление сессий имеет пуассоновское распределение, а число элементарных запросов в сессии подчиняется логарифмически-нормальному закону. Предложенная методика определения длительности пользовательских сессий позволит определить их величину, начиная с которой следует ограничивать доступ к сайтам пассивных пользователей, что может повысить финансовую пропускную способность центра обработки данных до 30 % .

 

Литература.

 

1.                  Menascé D., Almeida V., Fonseca R., Mendes M. A Methodology for Workload Characterization of E-commerce Sites, Proc. Of ACM E-COMMERCE 99.

2.                  Menascé D., Almeida V., Fonseca R., Mendes M. Business-oriented resource management policies for e-commerce servers, Performance Evaluation 42 (2000), pages 223–239.

3.                  Liu Z., Niclausse N., Jalpa-Villanueva C. Web traffic modeling and performance comparison between HTTP 1.0 and HTTP 1.1. Systems Performance Evaluation: Methodologiesand Applications. CRC Press, 2000, pages 177–189.

4.                  Абезгауз Г.Г., Тронь А.П., Копенкин Ю.Н., Коровина И.А. Справочник по вероятностным расчетам. — М.: Воениздат, 1966.

5.                  Дунин-Барковский И.В., Смирнов Н.В. Теория вероятностей и математическая статистика в технике. — М.: Гостехиздат, 1955.

6.                  Павловский З. Введение в математическую статистику. — М.: Статистика, 1967.

 

Поступила в редакцию 14.08.2008 г.