Математическое моделирование динамики городской застройки

с помощью клеточных автоматов

Арзамасцев Александр Анатольевич,

доктор технических наук,

Соломина Ольга Александровна,

аспирант кафедры компьютерного и математического моделирования

Тамбовского государственного университета им. Г.Р.Державина.

Управление развитием городской застройки является одной из наиболее важных и, в тоже время, трудно решаемых задач. Для обеспечения эффективного регулирования городских процессов, связанных с территориальным развитием города, необходимо использовать системный подход и математического моделирование.

Целью данной работы является разработка дискретной математической модели динамики городской застройки. Исследование пространственной организации города осуществляется с помощью программы-симулятора, основанной на методе клеточных автоматов [1]. Симулятор реализован в виде программного комплекса в среде разработки С++ Builder.

В качестве примера рассматривается динамика застройки территории города Тамбова. При моделировании использовались данные, полученные в [2].

Тушенка оптом

Крупнокусковые консервы ГОСТ от завода АРГО. Антикризисные цены!

tyshenka-optom.ru

Математическая модель имеет следующий вид.

G –дискретное метрическое множество размерности N´N; (i, j) – координаты ячейки,  0 £ i £ N, 0 £ j £ N,   NÎ. В данном случае N=110.

В начальный момент времени имеется 1 тип объектов – «объект застройки»

 ,                                                              (1)

где n – общее количество объектов типа А в начальный момент времени, n=10; (i_n, j_n) – индексы n-го объекта типа А, характеризующие расположение данного объекта на сетке.

Для каждого объекта должно выполняться неравенство:

"l,m:,  А_l,А_m      |i_l – i_m| + |j_l – j_m| > 0,                                                               (2)

которое означает, что каждый объект в системе имеет отдельную ячейку.

Выбор параметров объектов типа А в начальный момент времени осуществляется в соответствии с выражением:

 {n, l, l^max, r, v, τ, n^reg }                                                                               (3)

где  n- количество объектов заданного типа; l- возраст объектов в начальный момент времени; l^max  - максимальная продолжительность жизни объектов;  r – шаг перемещения объектов; v - диапазон обзора объекта; τ - период регенерации объектов; n^reg - количество появляющихся объектов за 1 итерацию при регенерации.

В данном случае объекты не перемещаются, т.е. r=0. Диапазон обзора не задаем (v=0). Продолжительность жизни l^max Î(200;400), а l=0.

,                                                                   (4)

(l)_t  ³ l^max Þ А = А – {А_n},                                                                              (5)

Выражение (4) определяет изменение возраста объекта. Выражения (5) позволяют исключить объект из множества объектов системы, если отведенный ему максимальный срок жизни уже истек.

                                                                  (6)

 {l, l^max, r, v, τ, n^reg },                                                                                   (7)

Увеличение количества объектов в множестве объектов типа А определяется выражением (6). При этом определение параметров нового объекта происходит в соответствии с выражением (7).

Наиболее вероятностным подходом к рассмотрению хронологической последовательности расширения городской территории является учет ландшафтных особенностей местоположения города. Для обозначения рек, водоемов и мест непригодных для строительства по своим топографическим особенностям используются «мертвые» зоны – ограниченные части сетки, в которых не возможно появления объектов при регенерации. «Мертвые» зоны могут стать зонами «притяжения», если им задать коэффициент притяжения (начиная с 0). Зоны «притяжения» влияют на расположение объектов при регенерации. Поэтому «мертвые» зоны появляются на сетке с 0 итерации и имеют коэффициент притяжения. В данном случае это будут зоны, обозначающие Тамбовское водохранилище, канал реки Цны, река Студенец и часть сетки справа от канала реки Цны, так как правый берег реки Цны является низменным и заливным и не может служить строительной площадкой.

Для определения мест на дискретной сетке, в которых будут располагаться зоны, используется карта Тамбова. При этом масштаб соблюдается и зоны строятся с учетом того, что сторона каждой ячейки составляет 87.5 м. Точку, от которой начинается регенерация объектов, обозначающую место начала строительства крепости, зададим координатами (75,51).

Зоны, обозначающие часть реки Студенец и часть канала реки Цны, расположенные ближе к начальной точке регенерации, имеют высокие коэффициент притяжения. Зонам, обозначающим оставшуюся часть канала реки Цны, присвоим более низкие коэффициенты притяжения.

Строительство линии ж/д дороги Москва-Саратов в конце 1860-х гг., прошедшей через Тамбов, оказало несомненное влияние на последующий характер формирования городской планировки. Для обозначения железной дороги также будем использовать зоны и задавать им коэффициенты притяжения.

Для управления темпами застройки территории воспользуемся тем, что при задании параметров регенерации объектов можно задавать количество объектов появившихся за одну итерацию и менять это количество с определенного номера итерации. Начиная со 154 итерации (соответствующей 1790 году) увеличим n^reg - количество объектов, появляющихся за 1 итерацию.

Для проверки адекватности данной модели рассмотрим соответствие результатов, полученных при моделировании, имеющимся планам города Тамбова (Рис. 1).

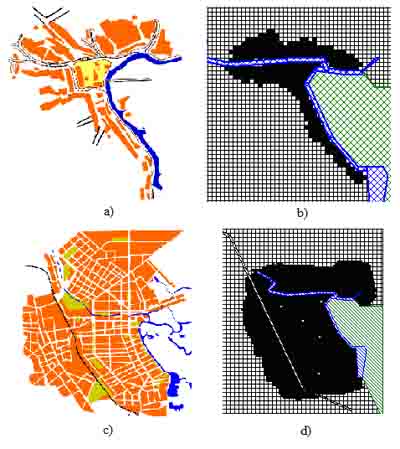
Рис.1. Сравнение результатов моделирования динамики городской застройки и картографических данных  в различные моменты времени: а), b) 1781 год и модель, полученная  на 145 итерации; c), d) 1989 год и модель, полученная  на 353 итерации.

Как видно из приведенного выше рисунка, данная модель позволяет получить достоверную информацию о динамике роста территории города.

Использование подобных моделей с учетом имеющихся ресурсных ограничений позволит вырабатывать более адекватные, более целесообразные решения в области стратегического управления городской застройкой.

Литература.

1.                  Соломина О.А., Арзамасцев А.А. Универсальный симулятор на основе клеточного автомата // Вестн. Тамб. ун-та. Сер. Естеств. и техн. науки. Тамбов, 2008. Т.13. Вып. 1. С. 109-111.

2.                  Горелов А.А. Историко-географические факторы застройки южной части г. Тамбова (1636г. – нач. XX века). Гуманитарные науки: проблемы м решения. Сборник научных статей / Под ред. А.А. Слезина. СПб.: Нестор, 2003.

Поступила в редакцию 06.10.2008 г.