Вычисление эксплуатационных характеристик физического принципа действия в энерго-информационной модели цепей при входных величинах, заданных четкими/нечёткими значениями

НА ГЛАВНУЮ

Хоменко Татьяна Владимировна,

кандидат технических наук,

Мурыгин Михаил Анатольевич,

аспирант Астраханского государственного технического университета,

Инженер-программист 1-ой категории ООО «Газпром добыча Астрахань».

В настоящее время одной из автоматизированных систем поиска новых технических решений, которая позволяет определять лучшие решения из полученных альтернатив, является система «Интеллект». Однако выбор лучших вариантов проводится по совокупности эксплуатационных характеристик, значения которых определены экспертами в скалярной форме, что не всегда возможно, в условиях увеличения требований к эксплуатационным характеристикам. В данной статье предлагается методика вычисление эксплуатационных характеристик физического принципа действия в энерго-информационной модели цепей, при входных величинах, заданных четкими/нечёткими значениями, что расширит возможности автоматизированные системы поиска новых технических решений.

В основу данной автоматизированной системы поиска новых технических решений «Интеллект» [1] положены энерго-информационные модели явлений различной физической природы. Разработанный единый математический аппарат включает описания физико–технических эффектов (ФТЭ) и получение физического принципа действия (ФПД) в виде последовательно совместимых ФТЭ [2]. Описания каждого ФТЭ представлены в виде паспорта, где указаны значения шести эксплуатационных характеристик (ЭХ) в виде точной количественной оценки. Значения ЭХ определены экспертами и носят субъективный характер. Однако, показано, что ЭХ представимы как в виде нечёткой переменной, так и в виде лингвистической переменной [3].

Таким образом, определяется задача вычисления ЭХ, заданных в различной форме для дальнейшего процесса принятия решения в области проектирования.

Результатом вычисления формул, при входных нечётких множеств, является нечеткое множество. Исходя из полученного нечеткого множества и исходных данных входных величин, необходимо определить нечеткую/лингвистическую переменную, которая и будет представлять собой значение эксплуатационной характеристики ФПД в ЭИМЦ.

Согласно [4], бинарной операцией на нечетком множестве называется отображение .

Пусть:

– F1, F2/L1, L2 – две нечеткие/лингвистические переменные;

– и – степень принадлежности (функция принадлежности) элемента a и b, соответственно, нечеткому множеству и , характеризующие нечеткие/лингвистические переменные;

– и носители нечетких множеств и .

Тогда:

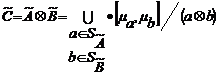(1)

– бинарная операция, осуществляемая над нечеткими множествами и ,

где: – нечёткое множество;

– операция, выполняемая над элементами нечетких множеств и , характеризующих нечеткие/лингвистические переменные F1, F2/L1, L2;

– свертка, выполняемая над значениями функций принадлежности.

Используемый в данной работе вариант свертки функций принадлежности:

является наиболее жестким вариантом, поскольку он не допускает компенсации низких значений одной функции принадлежности за счет другой.

Такой подход к определению арифметических операций является прямым, соответствующим непосредственно базовым основам теории нечетких множеств и сводящимся к оперированию с функциями принадлежности.

Случай 1. Входная величина:

скалярная оценка – нечёткая переменная F.

Выходная величина: нечёткая переменная F.

Согласно определению, для описания нечеткой переменной F необходимо определить тройку :

– нечеткое множество, характеризующее нечеткую переменную F, есть результат соответствующего вычисления по формуле (1).

X – универсальное множество есть результат арифметической операции над универсальным множеством входной нечеткой переменной F и скалярного значения k, соответствующей той, которая выполнялась над нечеткой переменной F и скалярным значением k. Универсальное множество в этом случае будем рассматривать как некоторый интервал:

N – имя полученной нечеткой переменной есть результат применения правил определения имени нечеткой переменной.

Имя N нечёткой переменной F заносится в паспорт ФПД, остальные элементы кортежа, описывающие нечёткую переменную, заносятся в базу знаний автоматизированной системы поиска новых технический решений и, в дальнейшем, используются для ранжирования.

Случай 2. Входная величина:

скалярная оценка – лингвистическая переменная L.

Выходная величина: нечёткая переменная F.

В качестве результата будем рассматривать получение нечёткую переменную F, а не лингвистическую переменную L, так как к полученному в результате нечеткому множеству сложно будет подобрать эквивалентный терм.

Согласно определению, для описания нечеткой переменной F необходимо определить тройку :

X – универсальное множество есть результат арифметической операции над универсальным множеством входной лингвистической переменной L и скалярного значения k, соответствующей той, которая выполнялась над нечеткой переменной L и скалярным значением k. Универсальное множество в этом случае будем рассматривать как некоторый интервал:

Случай 3. Входная величина:

нечеткая переменная F1 – нечеткая переменная F2.

Выходная величина: нечеткая переменная F.

Согласно определению, для описания нечеткой переменной F необходимо определить тройку :

X – универсальное множество есть результат арифметических операций над универсальными множествами входных нечетких переменных F1 и F2, соответствующих тем, которые выполнялись над нечеткими переменными F1 и F2. Универсальные множества в этом случае будем рассматривать как некоторые интервалы:

N – имя полученной нечеткой переменной есть результат применения правил определения имени нечеткой переменной *, описанному во второй главе.

Случай 4. Входная величина:

нечёткая переменная F – лингвистическая переменная L.

Выходная величина: нечеткая переменная F.

Согласно определению, для описания нечеткой переменной F необходимо определить тройку :

X – универсальное множество есть результат арифметических операций над универсальными множествами входных нечетких переменных F и L, соответствующих тем, которые выполнялись над нечеткими переменными F и L. Универсальные множества в этом случае будем рассматривать как некоторые интервалы:

Случай 5. Входная величина:

лингвистическая переменная L1 – лингвистическая переменная L2.

Выходная величина: лингвистическая переменная L.

Согласно определению, для описания лингвистической переменной L необходимо определить кортеж :

– нечеткое множество, характеризующее лингвистическую переменную L, есть результат соответствующего вычисления по формуле (1).

X – универсальное множество есть результат арифметических операций над универсальными множествами входных лингвистических переменных L1 и L2, соответствующих тем, которые выполнялись над лингвистическими переменными L1 и L2. Универсальные множества в этом случае будем рассматривать как некоторые интервалы:

T, G, M – элементы кортежа, характеризующие лингвистическую переменную L есть элементы кортежа исходных лингвистических переменных L1 и L2, так как термы, описывающие значения лингвистических переменных, должны строится из одних и тех же базовых термов и подчиняться тем же синтаксическим и семантическим правилам.

N – имя лингвистической переменной L есть терм, описывающий значение данной лингвистической переменной.

Однако получить терм – имя лингвистической переменной L, непосредственно из результирующего нечеткого множества , полученного в результате соответствующих вычислений, не представляется возможным.

Для получения такого терма необходимо определить наиболее соответствующее результирующему нечеткому множеству сочетание базовых термов и модификаторов.

Имя N лингвистической переменной L заносится в паспорт ФПД, остальные элементы кортежа, описывающие лингвистическую переменную, заносятся в базу знаний автоматизированной системы поиска новых технический решений и, в дальнейшем, используются для ранжирования.

В разрабатываемой системе «Выбор лучших технических решений» ранжирование полученных альтернатив и выбор лучших решений проводится по шести ЭХ, значения которых рассчитываются по предложенной методике и которые возможно задать как в точной количественной форме, так и в лингвистической форме.

Реализация такой системы позволит, во-первых, расширить возможности представления значений ЭХ ФТЭ, во-вторых, применять разработанную систему на ранних этапах проектирования технических объектов.

Литература.

1. Зарипов М.Ф., Петрова И.Ю. Предметно-ориентировання среда для поиска новых технических решений «Интеллект». /IV Санкт-Петербургская международная конференция «РИ-95», С. - Пб.,1995,с.60-61.

2. Зарипов М.Ф., Зайнуллин Н.Р., Петрова И.Ю. Энерго-информационный метод научно-технического творчества / Учебно-методическое пособие /М.: ВНИИПИ, 1998. – 124 с.

3. Использование лингвистических переменных в качестве значений эксплуатационных характеристик физико-технических эффектов. М.А. Мурыгин, Т.В. Хоменко.

4. Научно-технический журнал «Прикаспийский журнал: управление и высокие технологии» Астрахань: Издательский дом «Астраханский университет», 2008. № 1(1), стр.89-91.

5. Нечеткие множества в моделях управления и искусственного интеллекта. /Под ред. Д.А.Поспелова. - М.: Наука. Гл. ред. физ.-мат. лит., 1986. - 312 с.

6. Поспелов Д.А. Логико-лингвистические модели в системах управления. - М.: Энергоиздат, 1981. - 232 с.

Поступила в редакцию 05.11.2008 г.