Преобразователи
динамического диапазона звуковых сигналов на основе
модулирующих
функций
Харитонов
Владимир Борисович,
кандидат технических
наук, профессор,
Зирова
Юлия Константиновна,
аспирант кафедры звукотехники,
Санкт-Петербургский
государственный университет кино и телевидения.
Преобразование динамического диапазона
звуковых сигналов на основе модулирующих функций в теории модуляционного
анализа-синтеза является безынерционным. Причем речь идет не о нелинейной обработке
мгновенных значений сигнала, которая обладает безынерционностью, но вносит в
обработанный сигнал нелинейные искажения. Обработка сигналов по их модулирующим
функциям теоретически в ряде случаев решает проблему преобразования
динамического диапазона сигналов без внесения в них искажений. На практике, как
отмечают авторы [1], выполнившие аналоговую реализацию устройств обработки
модулирующих функций, невозможно добиться теоретических результатов из-за
ограниченной точности и нестабильности параметров аналоговых устройств
выделения и обработки модулирующих функций. В данной статье изложены результаты
исследования цифровой реализация устройства преобразования динамического
диапазона на теоретической основе модуляционного анализа-синтеза, позволившей
выяснить потенциал метода средствами точной цифровой обработки сигналов.
Изначально преобразователи динамического
диапазона (ПДД) звуковых сигналов применялись в радиовещании для защиты
звуковых трактов от перегрузок, согласования диапазона уровней сигналов с динамическим
диапазоном каналов, по которым они передаются, и ослабления влияния шума
носителей записи. По схожим причинам компрессировали звук для
кинематографического канала звукопередачи, поскольку динамический диапазон
аналоговых фотофонограмм, как правило, составляет 35–45 дБ, а диапазон уровней звуковой
программы (воспринимаемый слухом) может достигать почти 110 дБ. Часто прибегают
к компрессированию как речи, так и музыки для сглаживания динамики звука и
повышения разборчивости речи на «живых» выступлениях, когда, например, выступающий
по каким-то причинам значительно удаляется от микрофона или приближается к
последнему. Можно привести еще много примеров применения только амплитудных компрессоров.
Но преобразование динамического диапазона не ограничивается его сжатием, а
включает еще лимитирование, шумоподавление и экспандирование звуковых сигналов.
Все эти виды обработки звука сейчас широко применяются и предположительно еще
долгое время будут помогать звукорежиссерам воплощать их творческие идеи и
решать технические задачи.
Некоторые причины включения ПДД в звуковые
тракты с переходом к цифровым способам записи потеряли свою актуальность: динамический
диапазон цифровых носителей записи и звуковых трактов сопоставим с динамическим
диапазоном человеческого слуха. Но в кинотеатре, если не сжимать динамический
диапазон звукового сопровождения кинофильма при его прослушивании, то тихие
фрагменты просто потонут в шумах зрительного зала. Также, если не ограничивать
верхнюю границу уровня сигнала, можно оглушить зрителей или перегрузить
усилители мощности и кинотеатральные громкоговорители. Таким образом, преобразование динамического диапазона кинематографического
звука необходимо для обеспечения комфортного прослушивания в зале кинотеатра. В
формате цифрового звука Dolby Digital, применяемом для
записи фонограмм большинства современных фильмов, предусмотрено формирование
специального сигнала управления динамическим диапазоном. В аппаратуре
воспроизведения предусмотрено использование этого сигнала для регулирования
динамического диапазона, причем имеется возможность изменения степени
компрессирования в зависимости от условий конкретного зрительного зала. В связи
с этим сохраняет актуальность разработки преобразователей динамического
диапазона, обеспечивающих высокое качество обработки звуковых сигналов при минимальном
вмешательстве звукооператора.
шины armour-shina.ru
По критерию быстродействия ПДД делятся на две
группы: инерционные (с динамически изменяющимся коэффициентом передачи) и
безынерционные (мгновенного действия).
Инерционные преобразователи используются в звукотехнике
уже в течение многих десятилетий, принцип их работы, достоинства и недостатки
достаточно подробно описаны в литературе [2; 3]. Их работа основана на
выделении из сигнала огибающей, формировании на основе огибающей управляющего
сигнала и последующем перемножении этих двух сигналов: входного звукового и
управляющего:
![]() ,
,
где ![]() – входной сигнал,
– входной сигнал, ![]() – управляющий сигнал,
– управляющий сигнал, ![]() – выходной сигнал.
– выходной сигнал.
Перемножению во временной области
соответствует свертка спектров названных сигналов в частотной области.
![]() ,
,
где ![]() – частотный спектр
входного сигнала,
– частотный спектр
входного сигнала, ![]() – частотный спектр
управляющего сигнала,
– частотный спектр
управляющего сигнала, ![]() – частотный спектр
выходного сигнала.
– частотный спектр
выходного сигнала.
Для формирования сигнала управления
применяется низкочастотная фильтрация максимальных или среднеквадратичных
значений входного сигнала. В результате такой фильтрации сигнал управления изменяется
инерционно, по отношению к изменениям амплитудного или среднеквадратичного
значения сигнала. Из-за противоречивости требований, предъявляемых к фильтрации
функции коэффициента передачи, возникают недостатки инерционных
преобразователей:
·
плавное
нарастание сигнала управления приводит к выбросам выходного сигнала при резком
увеличении сигнала на входе. Эти выбросы могут выйти за пределы линейного
участка характеристики передачи звукового тракта. При этом появятся нелинейные
искажения;
·
резкое
нарастание сигнала управления избавит от выбросов, но в то же время сигнал управления
приобретет крутой фронт – это обогатит его спектр, а значит, после свертки спектров
входного сигнала и сигнала управления значительно обогатится спектр выходного
сигнала. Это обусловит появление слышимых эффектов работы ПДД;
·
замедленный
процесс восстановления коэффициента передачи при резком уменьшении сигнала
приводит к появлению эффекта «дыхания шума паузы». Этот эффект выражается в
заметном на слух снижении громкости тихого фрагмента сигнала с постепенным
последующим ее увеличением;
·
резкое
восстановление коэффициента передачи обусловит появление пульсаций в управляющем
сигнале при обработке звукового сигнала с интенсивными низкочастотными
составляющими. Эти пульсации вызывают амплитудную модуляцию обрабатываемого
сигнала и приводят к появлению нелинейных искажений.
Для того чтобы перечисленные искажения не
были заметны на слух, необходимо подбирать оптимальные параметры фильтра для
определенного вида звукового материала: речи или музыки.
Известны безынерционные ограничители уровня
сигнала, в них ограничению подвергаются мгновенные значения сигнала,
превышающие некоторое заданное пороговое значение сигнала. При этом изменяется
форма сигнала и появляются большие нелинейные искажения, поэтому такие
устройства практически не используются. Их применяют, в основном, как средство
защиты от перегрузки тракта передачи сигнала.
Безынерционное преобразование динамического
диапазона звуковых сигналов на основе модулирующих функций в теории
модуляционного анализа-синтеза свободно от перечисленных недостатков
инерционных устройств и вышеупомянутых безынерционных ограничителей уровня
сигнала. В теории модуляционного анализа-синтеза все преобразования, в том
числе преобразование динамического диапазона, основываются на выделении из
сигнала и последующей обработки модулирующих функций: амплитудной и/или
частотной. Кроме преобразования динамического диапазона сигнала, на основе
модуляционных преобразований возможно осуществить: безынерционное управление
тембром звуковых сигналов [4], сжатие частотного диапазона звуковых сигналов на
основе выделения и нелинейной обработки их мгновенной частоты [5] и другие виды
преобразований [8].
Аналоговый безынерционный
компрессор на основе модулирующих функций оказался довольно сложным в реализации.
Результаты его работы, представленные в [6; 7], показывают, что все недостатки
инерционных компрессоров в данном случае отсутствуют. Но из-за ограниченной
точности и нестабильности параметров аналоговых устройств выделения и обработки
модулирующих функций результаты далеки от теоретически возможных. В связи со
сложностью аналоговой реализации, безусловно, огромный интерес представляет
создание цифрового безынерционного ПДД на основе модулирующих функций.
Во-первых, это позволит улучшить качество обработки звука за счет использования
алгоритмов преобразования динамического диапазона, недоступных или
труднореализуемых с необходимой точностью в аналоговой форме. Во-вторых, в
связи с повсеместным использованием цифровых способов записи, обработки и воспроизведения
звука наиболее естественно выполнять преобразование динамического диапазона
также в цифровой форме. Точная цифровая реализация ПДД на основе модуляционного
анализа-синтеза позволит в полной мере выяснить потенциальные возможности
метода, чему до сих пор препятствовали принципиально неустранимые погрешности
аналоговой реализации.
Перед изложением результатов
работы цифрового безынерционного компрессора имеет смысл рассмотреть подробнее
модулирующие функции и основы модуляционных преобразований сигналов.
Согласно теории модуляционного
анализа-синтеза, произвольный сигнал можно представить как результат
совместного применения амплитудной и частотной модуляции:
![]() ,
,
если удачно выбрать пару модулирующих функций
![]() – амплитудную модулирующую
функцию и
– амплитудную модулирующую
функцию и ![]() – частотную
модулирующую функцию. В теории доказано, что для однозначного выбора этой пары
функций необходимо исходный сигнал дополнить опорным с помощью преобразования
Гильберта. Понятия о модулирующих функциях сигнала были введены еще в
– частотную
модулирующую функцию. В теории доказано, что для однозначного выбора этой пары
функций необходимо исходный сигнал дополнить опорным с помощью преобразования
Гильберта. Понятия о модулирующих функциях сигнала были введены еще в
Огибающей (амплитудной модулирующей функцией)
пары сигналов, сопряженных по Гильберту ![]() , называют неотрицательную функцию времени
, называют неотрицательную функцию времени
![]() . (1)
. (1)
Мгновенной частотой (частотной модулирующей
функцией) пары сигналов ![]() называют производную
от текущей фазы:
называют производную
от текущей фазы:
![]()
Введенные Д. Габором понятия нашли широкое
применение при описании преобразований узкополосных сигналов.
Ю. М. Ишуткин в [8] предложил обобщить
введенные Д. Габором определения модулирующих функций, не накладывая
ограничений на ширину частотного спектра сигналов.
Идея обработки звукового сигнала путем
воздействия на его модулирующие функции, предложенная Ю. М. Ишуткиным, состоит
в том, чтобы:
1. По известному вещественному сигналу ![]() с помощью преобразования
Гильберта создать комплексный сигнал
с помощью преобразования
Гильберта создать комплексный сигнал
![]() ,
,
где ![]() – Гильбертово
отображение сигнала
– Гильбертово
отображение сигнала ![]() .
.
2. Для этой пары сигналов ![]() вычислить модулирующие
функции: амплитудную модулирующую функцию и частотную модулирующую функцию
сигнала.
вычислить модулирующие
функции: амплитудную модулирующую функцию и частотную модулирующую функцию
сигнала.
3. Преобразовать модулирующие функции в целях
обработки с помощью линейных и нелинейных цепей.
4. По измененным модулирующим функциям синтезировать
новый звуковой сигнал.
Совокупность первых двух операций, в
результате которых становятся известными модулирующие функции сигнала, называют
модуляционным анализом. Последняя операция носит название модуляционного
синтеза. Структура канала полного модуляционного анализа-синтеза представлена
на рис.1 [8].
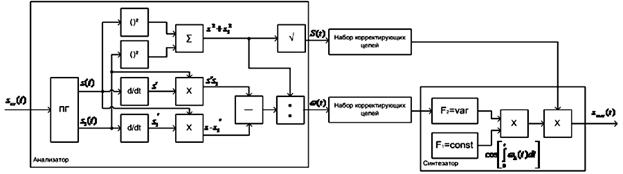
Рис.1.
Структура канала полного модуляционного анализа-синтеза.
Безынерционность преобразования динамического
диапазона достигается благодаря возможности полного доступа к амплитудной
модулирующей функции сигнала и непосредственному мгновенному воздействию на эту
функцию с целью создания требуемого вида преобразования динамического
диапазона. В зависимости от выбора функции воздействия на мгновенную амплитуду можно
реализовать любой вид ПДД: компрессор, лимитер, шумоподавитель, экспандер.
Поскольку для реализации преобразования динамического диапазона не нужно
воздействовать на частотную модулирующую функцию, то и нет никакой
необходимости в ее выделении. Это обстоятельство не только упрощает алгоритм
обработки, но и избавляет от решения нетривиальной задачи – устранения скачков
фазы сигнала, появление которых неизбежно при вычислении функции арктангенса. Таким
образом, помимо прочих операций, для безынерционного преобразования динамического
диапазона в первую очередь необходимо на стадии модуляционного анализа реализовать
преобразование Гильберта. Как отмечают авторы [1], выполнившие аналоговую
реализацию устройств модуляционного анализа-синтеза оказалось очень сложно
реализовать преобразование Гильберта с требуемой высокой точностью на
аналоговой элементной базе. Практическая деятельность по реализации
фазовращателей показала, что обеспечить получение теоретически возможной
точности фазового сдвига очень сложно. А погрешность приводит к искажениям
огибающей и паразитной амплитудной модуляции сигнала, которые сильно влияют на
качество звука. Кроме того, проблематично выполнить выделение амплитудной
модулирующей функции с сохранением динамического диапазона сигнала не уже 70–80 дБ.
Связано это с тем, что динамический диапазон существующих аналоговых
перемножителей не превышает 74–80 дБ. И если при вычислении огибающей
возвести в квадрат сигнал с динамическим диапазоном 80 дБ, то при идеальном
выполнении этой операции динамический диапазон должен удвоиться и составлять
160 дБ, из которых на выходе реального перемножителя, реализующего
операцию возведения в квадрат, останется только 80дБ, а после извлечения
квадратного корня – только 40дБ. Поэтому было предложено [1] отказаться от
вычисления амплитудной модулирующей функции непосредственно по формуле (1), а использовать
дополнительное преобразование. Таким дополнительным преобразованием является
перенос сигнала на высокую частоту с последующим выделением и обработкой
амплитудной модулирующей функции на высокой частоте.
Для построения цифровой
системы необходимо произвести требуемые преобразования цифрового представления
звукового сигнала. Цифровой безынерционный ПДД может быть построен по схеме с
прямым регулированием. С учетом дискретизации аналоговых сигналов его
структурная схема изображена на рис.2.
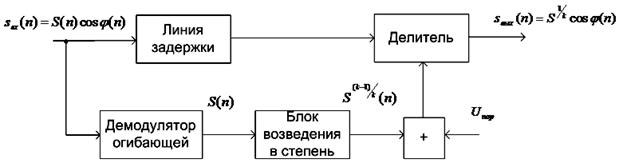
Рис.2. Структурная схема цифрового
безынерционного компрессора с прямым регулированием.
Исходный сигнал представлен
как
![]() ,
,
где ![]() — дискретная
мгновенная амплитудная модулирующая функция, а
— дискретная
мгновенная амплитудная модулирующая функция, а ![]() — дискретная
мгновенная фаза сигнала. В демодуляторе огибающей выполняется преобразование
Гильберта и вычисление амплитудной модулирующей функции. Частотный спектр
исходного сигнала, в соответствии со свойством спектра произведения образов,
будет равен
— дискретная
мгновенная фаза сигнала. В демодуляторе огибающей выполняется преобразование
Гильберта и вычисление амплитудной модулирующей функции. Частотный спектр
исходного сигнала, в соответствии со свойством спектра произведения образов,
будет равен
![]() , (2)
, (2)
где ![]() — частотный спектр
амплитудной модулирующей функции,
— частотный спектр
амплитудной модулирующей функции, ![]() — символ прямого преобразование
Фурье, его выполнение в данном выражении формирует в качестве второго операнда
свертки частотный спектр косинуса мгновенной фазы сигнала, а
— символ прямого преобразование
Фурье, его выполнение в данном выражении формирует в качестве второго операнда
свертки частотный спектр косинуса мгновенной фазы сигнала, а ![]() — частотный спектр
сигнала.
— частотный спектр
сигнала.
В результате нелинейного
преобразования мгновенной амплитудной модулирующей функции, выполняемого в
блоке возведения в степень, получаем новую дискретную амплитудную модулирующую
функцию ![]() , где
, где ![]() — некоторая нелинейная
функция, в данном случае — степенная, реализующая амплитудную характеристику
ПДД требуемого вида. Новой амплитудной модулирующей функции будет соответствовать
новый частотный спектр
— некоторая нелинейная
функция, в данном случае — степенная, реализующая амплитудную характеристику
ПДД требуемого вида. Новой амплитудной модулирующей функции будет соответствовать
новый частотный спектр ![]() . Частотный спектр синтезированного по измененной амплитудной
модулирующей функции сигнала будет иметь вид
. Частотный спектр синтезированного по измененной амплитудной
модулирующей функции сигнала будет иметь вид
![]() .
.
Введение линии задержки
необходимо для синхронизации исходного сигнала с сигналом огибающей, вычисление
которой неизбежно сопровождается временной задержкой.
Добавление к новой огибающей
постоянного сигнала ![]() необходимо для того, чтобы преобразование начиналось со
значения огибающей, превышающих пороговый уровень, задаваемый постоянным слагаемым.
необходимо для того, чтобы преобразование начиналось со
значения огибающей, превышающих пороговый уровень, задаваемый постоянным слагаемым.
Для частного случая реализации
амплитудной характеристики компрессора со сжатием динамического диапазона в два
раза сигнал на выходе безынерционного ПДД можно представить следующим соотношением:
![]() .
.
Выполнение большинства
требуемых математических операций цифровой системой осуществляется с высокой
точностью. Пожалуй, наиболее сложным элементом цифрового ПДД является широкополосный
цифровой преобразователь Гильберта (ЦПГ), входящий в состав блока демодуляции
огибающей. От него во многом зависит качество ПДД. Для достижения высокого
качества преобразования ЦПГ должен в широкой полосе частот, от 32 Гц до
16000 кГц, обеспечивать частотно-независимый фазовый сдвиг сигнала на ![]() с погрешностью порядка
с погрешностью порядка
![]() . Величина фазовой погрешности выбирается такой, чтобы
возникающие из-за нее пульсации мгновенной амплитуды тонального сигнала не были
заметны на слух. При такой фазовой погрешности их уровень не превысит
-80 дБ. Реализация такого преобразователя рассмотрена в [10].
. Величина фазовой погрешности выбирается такой, чтобы
возникающие из-за нее пульсации мгновенной амплитуды тонального сигнала не были
заметны на слух. При такой фазовой погрешности их уровень не превысит
-80 дБ. Реализация такого преобразователя рассмотрена в [10].
Компьютерная модель цифрового
безынерционного компрессора на основе модулирующих функций, построенная по
схеме рис.2, при проверке работоспособности на тестовых однотональных сигналах
дала положительные результаты, показав тем самым правильность найденных
алгоритмических решений, а также успешное решение проблем, неизбежно возникающих
при переходе от аналогового представления сигналов к цифровому. Амплитудная
модулирующая функция исходного однотонального сигнала представляет собой
постоянную функцию времени. В результате нелинейного преобразования амплитудной
модулирующей функции получается новая временная амплитудная модулирующая
функция, но в случае с однотональным сигналом это будет снова постоянная
функция времени. Спектр исходной амплитудной модулирующей функции и нелинейно
преобразованной для однотонального сигнала состоит из одной гармоники на
частоте сигнала. Результат свертки синтезированного по измененной амплитудной
модулирующей функции однотонального сигнала заведомо будет подобен по форме
исходному сигналу.
Проверка работы
безынерционного ПДД на реальном звуковом сигнале дала неожиданные результаты, а
именно временами очень плохое качество звука прошедшего нелинейную обработку.
Для поиска причины, вызывающей заметные на слух артефакты при прослушивании обработанного
сложного звукового сигнала, был выполнен анализ форм модулирующих функций (сравнение
значений на выходе цифровой модели с расчетными значениями), а также
сопоставление форм их частотных спектров. В качестве тестового сигнала ![]() для такой проверки был
выбран сигнал, состоящий из двух гармонических компонентов с частотами
для такой проверки был
выбран сигнал, состоящий из двух гармонических компонентов с частотами ![]() Гц и
Гц и ![]() Гц:
Гц:
![]() ,
,
где, ![]() — частота
дискретизации сигнала, равная 44 100Гц.
— частота
дискретизации сигнала, равная 44 100Гц.
Ниже приведена расчетная
временная диаграмма тестового сигнала ![]() и его частотный спектр
(рис. 3а), а также временные диаграммы и частотные спектры его амплитудной
модулирующей функции (рис. 3б) и косинуса фазы (рис. 3в). Спектры амплитудной
модулирующей функции и косинуса фазы состоят из множества компонент, но в
результате свертки таких спектров остаются всего две составляющие.
и его частотный спектр
(рис. 3а), а также временные диаграммы и частотные спектры его амплитудной
модулирующей функции (рис. 3б) и косинуса фазы (рис. 3в). Спектры амплитудной
модулирующей функции и косинуса фазы состоят из множества компонент, но в
результате свертки таких спектров остаются всего две составляющие.
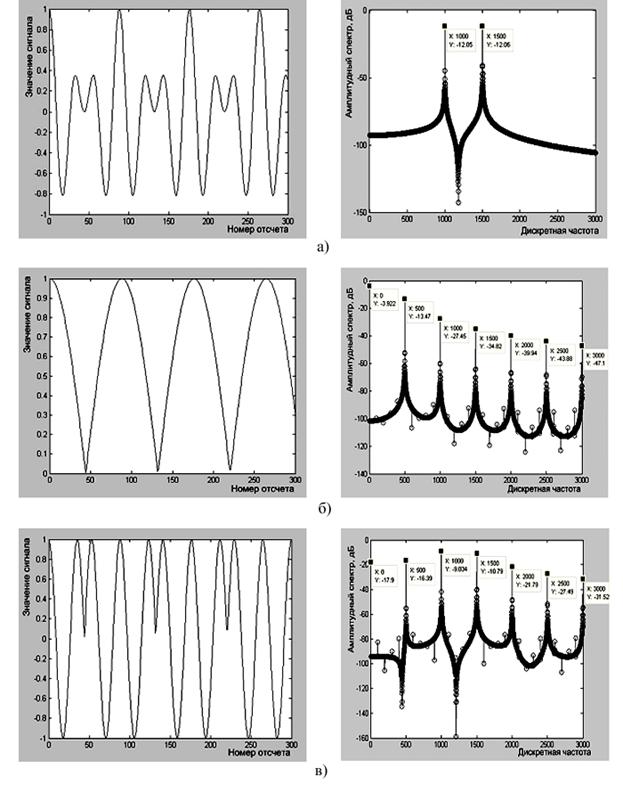
Рис.3. Временные функции (справа) и частотные спектры
(слева): а) сигнала биений с частотами 1000 и 1500Гц; б) амплитудной
модулирующей функции сигнала биений; в) косинуса фазы сигнала биений.
Аналитическое выражение для
временной амплитудной модулирующей функции имеет вид:
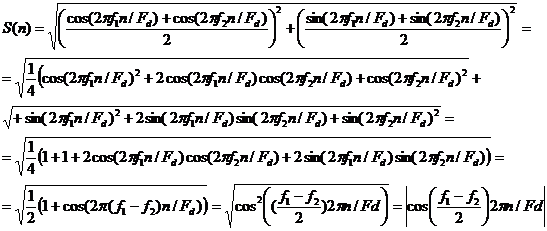
Для вычисления ее спектра
удобно воспользоваться табличным косинус-преобразованием Фурье [11] функции ![]() при
при ![]()
|
|
|
|
|
|
Табличные значения гамма-функции
![]() для аргументов в
диапазоне от 0 до 2, а также формулы для вычисления гамма-функции для больших и
отрицательных значений аргументов представлены в [12]. В таблице 1 сведены
результаты аналитического расчета спектральных составляющих амплитудной модулирующей
функции на угловых частотах
для аргументов в
диапазоне от 0 до 2, а также формулы для вычисления гамма-функции для больших и
отрицательных значений аргументов представлены в [12]. В таблице 1 сведены
результаты аналитического расчета спектральных составляющих амплитудной модулирующей
функции на угловых частотах ![]() от 0 до
от 0 до ![]() с периодом равным
с периодом равным ![]() . В дискретной области частоте
. В дискретной области частоте ![]() соответствует частота
соответствует частота ![]() , равная отношению частоты дискретизации к количеству
отсчетов на периоде сигнала. Практически полное совпадение значений,
обозначенных на диаграммах рис. 3, с результатом аналитического расчета
подтверждает правильность построений рис. 3.
, равная отношению частоты дискретизации к количеству
отсчетов на периоде сигнала. Практически полное совпадение значений,
обозначенных на диаграммах рис. 3, с результатом аналитического расчета
подтверждает правильность построений рис. 3.
Таблица 1.
Аналитические значения спектра амплитудной
модулирующей функции.
|
|
Дискретная
частота |
|
|
0 |
0 |
–3,93 |
|
|
500 |
–13,47 |
|
|
1000 |
–27,45 |
|
|
1500 |
–34,82 |
|
|
2000 |
–39,94 |
|
|
2500 |
–43,88 |
|
|
3000 |
–47,1 |
Сжатию динамического диапазона
в два раза соответствует степенная обработка амплитудной модулирующей функции с
показателем степени равным 1/2. Для этого случая на рис. 4 показаны различия временных
функций и частотных спектров исходного (штриховая линия) и обработанного (сплошная
линия) сигналов (рис. 4а), а также их амплитудных модулирующих функций (рис.
4в). Спектры исходных и обработанных сигналов сдвинуты на диаграмме относительно
друг друга на 30 отсчетов для более наглядного представления их различий.
В табл. 2 представлены
результаты аналитического расчета спектра нелинейно преобразованной огибающей,
вычисленные по формуле (3) для ![]() . Они практически точно совпадают со значениями,
обозначенными на диаграммах рис. 4, что подтверждает точность последних.
. Они практически точно совпадают со значениями,
обозначенными на диаграммах рис. 4, что подтверждает точность последних.
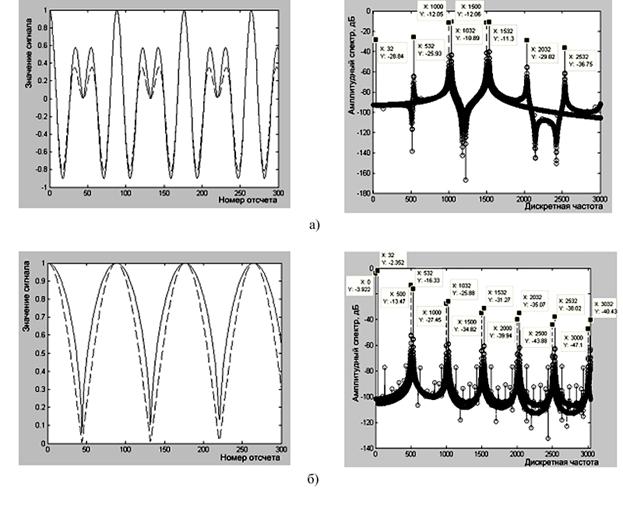
Рис.4. Временные функции (справа) и частотные спектры
(слева): а) сигналов на входе и выходе безынерционного преобразователя; б)
амплитудной модулирующей функции входного сигнала и результата ее степенной
обработки.
Таблица 2.
Аналитические значения спектра нелинейно
преобразованной амплитудной модулирующей функции (степень 1/2).
|
|
Дискретная
частота |
|
|
0 |
0 |
-2,35 |
|
|
500 |
-16,33 |
|
|
1000 |
-25,87 |
|
|
1500 |
-31,25 |
|
|
2000 |
-35,03 |
|
|
2500 |
-37,95 |
|
|
3000 |
-40,33 |
Нелинейное преобразование
амплитудной модулирующей функции видоизменило ее спектр (рис. 3б). В результате
свертки такой нелинейно преобразованной огибающей и входного сигнала выходной
сигнал будет иметь существенно обогащенный спектр по сравнению со входным (рис.
3а). В синтезированном по измененной огибающей сигнале биений появятся
дополнительные составляющие, которые можно рассматривать как интермодуляционные
искажения. Они меняют субъективное восприятие преобразованного сигнала. Очевидно,
что в любом другом случае, кроме обработки однотонального сигнала, из-за изменения
только одного из операндов в выражении (2) будет получен спектр преобразованного
сигнала, отличающийся от исходного. Степень обогащения спектра выходного
сигнала зависит от широкополосности огибающей: чем шире спектр нелинейно преобразованной
огибающей, тем сильнее обогащается частотный спектр преобразованного сигнала.
Таким образом, в чистом виде
безынерционное преобразование динамического диапазона звуковых сигналов на
основе модулирующих функций непригодно из-за изменений частотного спектра преобразованного
сигнала, в ряде случаев, отчетливо заметных на слух. Можно, конечно,
отфильтровать спектр нелинейно преобразованной огибающей, примерно до ширины
критической полосы слуха в низкочастотной части звукового диапазона. Тогда
дополнительные составляющие окажутся в
пределах одной критической полосы с составляющими спектра исходного
сигнала и окажутся замаскированными. Но ПДД при этом потеряет свойство
безынерционности из-за ограниченной длительности переходной функции фильтра мгновенной
огибающей.
Выводы:
·
Цифровая
модель ПДД позволила избавиться от неустранимых погрешностей аналоговой
реализации и выяснить потенциальные возможности метода ПДД на основе нелинейной
обработки модулирующих функций.
·
Прослушивание
фонограмм после обработки цифровым ПДД на основе модулирующих функций обнаружило
возникновение в некоторые моменты слышимых грубых искажений звукового сигнала.
·
Анализ
временных функций и частотных спектров сигналов, возникающих при ПДД с использованием
модулирующих функций, позволил объяснить возникновение слышимых искажений обогащением
частотного спектра обработанного сигнала вследствие изменения спектра
амплитудной модулирующей функции. Для уменьшения заметности искажений
необходимо фильтровать преобразованную амплитудную модулирующую функцию. При
этом ее спектр сужается, и при условии, что дополнительные составляющие
оказываются в одних критических полосах слуха с основными составляющими, первые
эффективно маскируются вторыми. Правда при этом ПДД теряет свойство безынерционности.
·
В связи
с наличием у безынерционных ПДД на основе модулирующих функций принципиальных
недостатков, представляется, что создание более совершенных ПДД должно идти по
пути улучшения инерционных преобразователей.
Литература.
1.
Основы
модуляционных преобразований звуковых сигналов: Монография/ Ишуткин Ю. М., Уваров
В. К.; Под ред. В. К. Уварова. – СПб.: СПбГУКиТ, 2004.
2.
Радиовещание и
электроакустика: Учебник для вузов/ А. В. Выходец, М. В. Гитлиц,
Ю. А. Ковалгин и др.; Под ред. М. В. Гитлица. – М.: Радио и
связь, 1989.
3.
Udo Zoelzer. Digital Audio Signal Processing. John
Willey & Sons.
4.
Осташевский Е. Н.
Разработка метода и аппаратуры управления нестационарными фазами сигналов для
преобразования тембра при создании звуковых эффектов: Автореф. дис. канд. тех.
наук. – Л.: ЛИКИ, 1987.
5.
Уваров В. К.
Точное компандирование частотного и динамического диапазонов звуковых сигналов.
– СПб.:СПбГУКиТ, 2002.
6.
Плющев В. М.
Разработка метода и устройств безынерционного преобразования динамического
диапазона звуковых сигналов: Автореф. дис. канд.тех.наук. –Л.: ЛИКИ, 1986.
7.
Применение
модуляционных преобразований звуковых сигналов: Монография/ В. К. Уваров,
В. М. Плющев, М. А.
Чесноков; Под ред. В. К.
Уварова – СПб.:СПбГУКиТ, 2004.
8.
Перспективы
обработки звуковых сигналов по их модулирующим функциям. Ишуткин Ю. М. Труды Ленинградского института
киноинженеров, ![]() . –с. 102-115.
. –с. 102-115.
9.
D.Gabor, J.IEE 93, (pt3), (1946).
10.
Журнал научных
публикаций аспирантов и докторантов, ISSN 1991-3087,
11.
Интегральные
преобразования и операционное исчисление, В. А. Диткин, А. П. Прудников, Главная редакция
физико-математической литературы изд-ва «Наука», М.,
12.
Справочник по
математике (для научных работников и инженеров). Г. Корн, Т. Корн. – М., 1977.
Поступила в редакцию 16.10.2008
г.
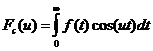
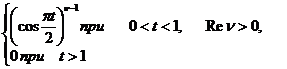
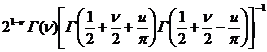 (3)
(3)