УДК 621.755 - 251

Методика определения величины и места расположения неуравновешенности по сигналам от дисбаланса.

Кочкин Сергей Вячеславович,

аспирант кафедры «Автоматика и телемеханика» Пензенского Государственного Университета,

старший научный сотрудник ООО «НПП «Техника», г. Пенза.

При измерении дисбаланса в балансировочных устройствах измерительной задачей является определение величины и угловой координаты расположения неуравновешенности по сигналам от дисбаланса.

Известен способ определения величины и угловой координаты расположения неуравновешенности, использующий разложение сигнала в ряд Фурье. [1] По основным амплитудам гармоник вычисляются величины неуравновешенности, а по полученной фазе этих гармоник – угловая координата расположения неуравновешенности.

Несмотря на очевидную простоту, этот метод имеет два существенных недостатка:

- метод не учитывает неравномерности периодов колебаний внутри измерений, которые в случае балансировки в режиме сферического циркуляционного движения при различных типах привода составляет от 0,1 до 3 %;

- метод сложен с вычислительной точки зрения при реализации его ограниченными средствами микроконтроллера.

Поэтому предлагается применять в случае балансировки в вибрационных режимах алгоритм определения величины и места расположения неуравновешенности в отдельных периодах.

На рисунке 1 показан метод определения величины и угловой координаты места расположения неуравновешенности без разложения в гармонический ряд.

Рис. 1.

Определение величины и угловой координаты расположения неуравновешенности.

Метод заключается в разбиении всего сигнала на отдельные периоды, определение параметров неуравновешенности в каждом периоде и усреднения полученных значений.

Для реализации этого метода предлагается следующий алгоритм:

I. Делается допущение о том, что сигнал является гармоническим или близким к нему на одном периоде. Сигнал центрируется относительно оси X по формуле:

, где   - центрированный относительно оси X одномерный массив значений.

II. На периодический сигнал накладывается импульс опорного сигнала. При этом не критично, какой фронт опорного сигнала – восходящий или нисходящий используется для этого. Важно, чтобы всегда это был один и тот же фронт.

III. Из сигнала выделяется первый синусоидальный период. Например, перебором  значений ищется самый первый член ряда значений с координатой  с учетом условия увеличения значений при движении вправо (синусоидальный сигнал). Затем находятся два следующих пересечения с осью Х. Интервал  есть искомый период данного колебания. Значения этого периода сохраняются в , а индексы (количество отсчетов) – в Т. Дальнейшие операции проводятся именно с этими данными.

IV. Измеряется фазовый сдвиг  (количество отсчетов) между началом сигнала и рабочим фронтом импульса опорного сигнала. По величине этого фазового сдвига определяется угловая координата места расположения неуравновешенности по формуле .

V. По формуле  определяется амплитуда колебания. Эта амплитуда линейно (на определенном промежутке) соотносится с величиной неуравновешенности.

VI. После этого меняется текущий период на следующий, и операции по пп. IV-V повторяются n раз (n – количество периодов в измерении).

VII. Полученные результаты усредняются по формулам:

; .

VIII. Для определения истинного значения дисбаланса необходимо вычесть из вектора полученного дисбаланса вектор собственного дисбаланса устройства. Внешний вид этих значений вместе с полученными значениями дисбаланса показан на рисунке 2 в декартовых и в полярных координатах.

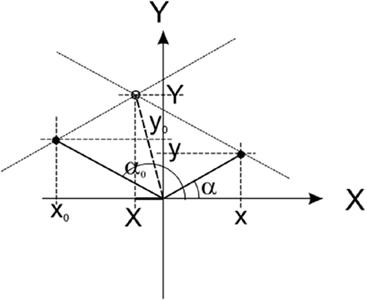
Рис. 2.

Вектор дисбаланса и вектор собственного дисбаланса.

Процедуру вычитания собственного дисбаланса удобней всего проводить не в полярных, а в декартовых координатах.

Перевод полученных значений дисбаланса в декартовы координаты производится по формулам: ,.

Проекции вектора истинного дисбаланса определяются по формулам:

, , где  и  параметры собственного дисбаланса устройства.

IX. Истинные значения величины и угловой координаты расположения дисбаланса в полярных координатах, связанных с осью балансируемого ротора, получаем по формулам:

, , где К – масштабный коэффициент, полученный при проведении процедуры масштабирования.

Проведя все подстановки, получаем параметры неуравновешенности:

,

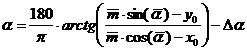, где  - коэффициент угловой коррекции, а именно, разница между положением датчика опорного сигнала и нулевой отметкой угловой шкалы (определяется при тарировке и масштабировании).

Для уменьшения величин ошибок предлагается проводить обработку полезного сигнала перед расчетом величины дисбаланса по приведенному алгоритму.

В данном случае стоит задача фильтрации с устранением быстрых (высокочастотных) составляющих, которые чаще всего обусловлены шумом либо помехами. В результате из высокочастотной зависимости получается другая, сглаженная зависимость, в которой доминирует низкочастотная составляющая. Наиболее простыми и эффективными способами сглаживания можно считать регрессию различного вида. Однако регрессия часто уничтожает информативную составляющую данных, оставляя лишь наперед заданную пользователем зависимость. [2] Поэтому более рационально использовать такие методики, как сглаживание. Сглаживание сигнала предлагается проводить на всем промежутке измерений, и только потом делить его на отдельные периоды с целью определения параметров неуравновешенности.

При выборе методики сглаживания был проведен анализ известных способов, таких, как сглаживание методом «бегущих медиан», локальное сглаживание адаптивным алгоритмом, основанное на анализе ближайших соседей каждой пары данных и др.

В результате сравнительного анализа методов сглаживания был выбран метод сглаживания всего сигнала функцией, использующей ядро функции Гаусса, которая вычисляет локально взвешенные средние значения исходного вектора.

На практике вычисление этой функции проводится по следующей формул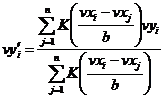е:  , где 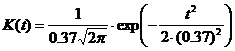; n – длина (количество отсчетов) вектора ; b – параметр сглаживания (рекомендуемое значение );  - частота дискретизации; - массив сглаженных данных, - массив равномерных временных отсчетов. [3]

Отдельной задачей является статистическая обработка результатов для определения промахов измерений. С целью повышения точности предлагается применять метод отбрасывания промахов на основе критерия Шовене. [4]

Для этого вводится понятие модуля отклонения от среднего значения в долях среднеквадратического отклонения Z. Воспользуемся формулами:, .

При проведении исследований сигналов было установлено, что наиболее рациональным методом является такой, при котором в случае выявления промаха в периоде отбрасывается только тот результат (масса или угловая координата), в котором обнаружен этот промах, а сопряженное с ним значение другой переменной не отбрасывается. Кроме этого было выяснено, что наименьшая погрешность измерительного устройства достигается при значении 1,9.

Предложенный метод опробован на устройствах для измерения параметров дисбаланса в режиме сферического циркуляционного движения и позволил проводить измерения с точностью около 6 мкм.

Литература.

1. Патент на изобретение РФ № 2003115472. Способ балансировки изделия/ М.М.Свиткин.

2. Сизиков В.С. Устойчивые методы обработки результатов измерений / Санкт-Петербург – Специальная литература, 1999, С.238.

3. Дьяконов В. Mathcad 2001 / Учебный курс, Санкт-Петербург – Питер, 2001, С.621.

4. Тейлор Дж. Введение в теорию ошибок / М – Мир, 1985, С.272.

Поступила в редакцию 14.04.2008 г.