Синтез уникальных фазоманипулированных сигналов для интеллектуальной системы обнаружения подвижных объектов

 

Бронов Сергей Александрович,

доктор технических наук,

Малеев Андрей Владимирович,

аспирант,

Михайленко Ярослав Витальевич,

аспирант,

руководитель группы АСУ Филиала ОАО «ФСК ЕЭС»- МЭС Сибири.

Сибирский федеральный университет.

 

Выбор зондирующих сигналов и способов обработки отраженных волновых полей, анализируемых различными системами обнаружения, на сегодняшний день остается трудной задачей. При ее рассмотрении приходится учитывать не только потенциальные возможности сигналов, но и решать технические проблемы создания реальных устройств.

Широкое практическое применение фазоманипулированных сигналов в системах обнаружения обусловлено; относительно равномерным распределением боковых лепестков корреляционной функции при большом числе дискретов на всей временной плоскости, постоянством амплитуды сигнала, а также простотой генерирования последнего.

У фазоманипулированных сигналов минимально достижимый уровень боковых лепестков обратно пропорционален чис­лу дискретов. Поэтому большее распространение получили фазоманипулированные сигналы с повышенным числом дискретов.

Существующие методы синтеза фазоманипулированных сигналов по желаемой форме тела неопределенности развиты недостаточно, поэтому на практике зачастую применяют конкретные коды, которые не являются оптимальными [3].

Для последовательности сигналов, состоящей из m им­пульсов (дискретов), при способе кодирования с помощью двух значений фазы можно синтезировать М = 2^m различных сиг­налов. Число дискретов равно m = Т/τ_и, где Т - дли­тельность дискрета (кодового знака). Практическое применение находят сигналы с числом дискретов от десятков до тысяч, а количество различных фазоманипулированных сигналов велико. Для построения требуемого сигнала, необходимо из 2^m кодовых комбинаций выбрать те, которые дают наи­лучшее приближение корреляционной функции к желаемой форме.

Огибаю­щая фазоманипулированного сигнала состоит из импульсов положительной и отрицатель­ной полярностей.

Взаимная корреляционная функция (ВКФ) разных сигналов описывает как степень сходства формы двух сигналов, так и их взаимное расположение друг относительно друга по координате (независимой переменной). Взаимная корреляционная функция двух различных сигналов s(t) и u(t), получается следующим скалярным произведением сигналов [3]:

B_su(t) =s(t) u(t+t) dt.

Взаимная корреляция сигналов характеризует определенную корреляцию явлений и физических процессов, отображаемых данными сигналами, и может служить мерой «устойчивости» данной взаимосвязи при раздельной обработке сигналов в различных устройствах.

Автокорреляционная функция (АКФ) финитного сигнала сигнала s(t), локализованного во времени и конечного по энергии, является количественной интегральной характеристикой формы сигнала, и определяется интегралом от произведения двух копий сигнала s(t), сдвинутых относительно друг друга на время t:

B_s(t) =s(t) s(t+t) dt.

Как следует из выражения, АКФ является скалярным произведением сигнала и его копии в функциональной зависимости от переменной величины значения сдвига t.

Сигналы, база которых изменяется в соответствии с кодом Баркера, являются уникальными фазоманипулированными сигнала­ми. Модуль их автокорреляционной функции имеет минимально достижимый одинаковый уровень боковых лепестков. В таблице 1 приведены значения кодов Баркера [4]. Огибающая и функция кор­реляции 13-позиционного сигнала Баркера изображены на рисунках 1а и 1б.

Есть сведения, что попытки найти коды Баркера для m>13 решения не имеют [2]. Таким образом, коды Баркера можно использовать лишь для сигналов с относительно неболь­шой базой.

С помощью разработанного программного комплекса, для системы обнаружения подвижных объектов [2, 1], был проведен поиск кодов с числом дискретов большим 13 (m>13). Следует отметить, что в результате синтеза не удалось получить фазоманипулированных сигналов аналогичных кодам Баркера, что подтверждает утверждение, сделанное в [5].

Однако с помощью разработанного программного комплекса были найдены уникальные коды для фазоманипулированных сигналов длиной более 13 периодов, имеющие, для данного числа дискретов, минимально достижимый уровень боковых лепестков функции корреляции (квази-коды Баркера).

Квази-коды Баркера с числом дискретов (14÷43) приведены в таблице 2. Следует отметить, что для каждого числа дискретов представленных в данной таблице уровень боковых лепестков нормированной корреляционной функции, является минимальным (рисунок 2). Уникальный код для каждого числа дискретов был рассчитан по адаптивного алгоритму с помощью высокопроизводительного компьютера.

 

 Таблица 1.

Значения кодов Баркера.

Число дискре­тов	Последовательность Баркера
2 4 4 5 7 11 13	1 -1 1 1 -1 1 1 1 1 -1 1 1 1 -1 1 1 1 1 -1 -1 1 -1 1 1 1 -1 -1 -1 1 -1 -1 1 -1 1 1 1 1 1 -1 -1 1 1 -1 1 -1 1

 

 

а)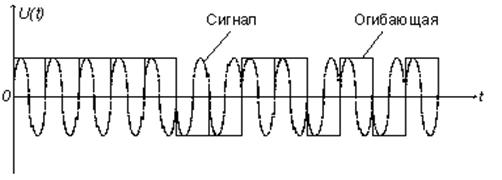     

б)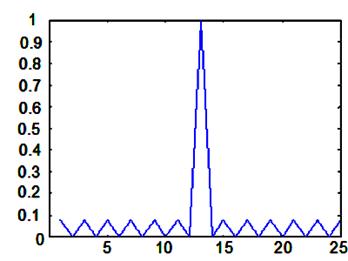

Рис. 1. а) огибающая 13-позиционного сигнала Баркера, б) корреляционная функция данного сигнала.

 

Таблица 2.

Уникальные коды для каждого числа дискретов.

Число дискретов	Уникальная последовательность
14	1111-11-111-1-111-1
15	11-111-11-11-1-1-1111
16	-1-11-11-1-1-1-1-111-1-111
17	1-11-1-111-1-1-1111111-1
18	11-1-1111-11-1-11-111111
19	-11-1-11-1-1-11-1-1-1111-1-1-1-1
20	1-1-1-111-11-11-1-111-111111
21	111111-11-1-1-11-111-1-1-111-1
22	111-1-11111111-1-11-1-11-11-11
23	1-1-11-111-11111-1111-11-1-1-111
24	1-1-11-1-1111111-1-1-111-1-1-11-11-1
25	111-1-1111-1-1-1-1-1-11-11-11-1-11-1-11
26	-1-11-1-1-1111-11111-11-1-111111-1-11
27	-1-1-1111-1-1111111-11-1-11-1-111-11-11
28	1-1-1111111-111-1-11-11-1111-1-11-11-1-1
29	-1-1111-11-1-1111-111111-111-1-11-11-1-11
30	1-1-1-111-1111-111111-1-1-11-111-111-11-1-1
31	-1-1-1-111-11111-1-111-1-111-11-1-1-1-11-11-1-1-1
32	1-1-111-111-11-1-1-1111-1-11-11-11111111-11-1
33	-1-1-1-1-111-1-111-111-1-11-11-1-11111-11-11-1111
34	1-11-1-11-1-111-1-1111-11-111-1-11111-1-1-1-1-11-11
35	1-1111-11-111111-11-1-11-11-1-1-1-11-111-1-111-1-1-1
36	11111-1-1-11-1-1111-1-1-11-11-1-11-111-1111-111-111
37	11-11-1-11-1-111111-1-111-1-1-11-1-1-1-1-1-11-11-1-1-1-111
38	-1-111-11-11-1-1-111-111-11-1-1-1-111-11-1-1-11-1-1-1-1-1-11-1
39	11-1-1111-11-1-11-111-1-11111111-1-1-1-1-1-11-11-11-1-1-11
40	1111-111-11-11-11-11-1-1-1-111111-1-111-1-111-111-11111
41	1111-1-1-1-11-111-111-1-111-11-1-1111-11-11-1111-11111-11
42	-111-1-11-1-11111-1-1-1-1-111-11111111-1111-11-111-1-1-111-1
43	-111-1-111-11-11111-11-11-1-111-111111-111-1-1-1-1-1-111-1-1-1-1

 

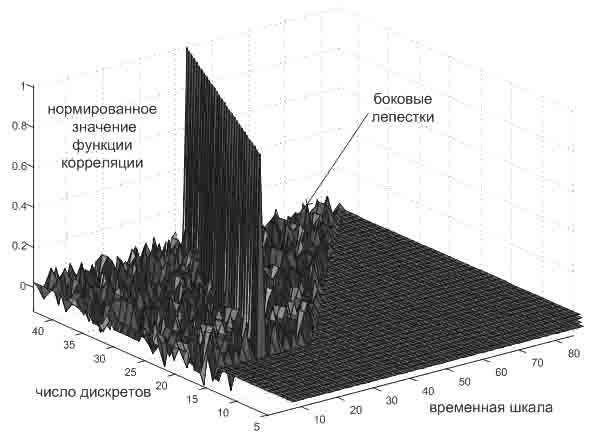
Рис. 2. Корреляционные функции фазоманипулированных сигналов.

 

Следует отметить, для определенных дискретов боковые лепестки корреляционной функции (рисунок 2) имеют значительные всплески (например, дискрет 40), поэтому при практическом применении полученных сигналов необходимо выбирать ближайший дискрет, уровень боковых лепестков которого меньше (например, дискрет 39 или 41).

С помощью разработанного программного комплекса найдены уникальные фазоманипулированные сигналы число дискретов в которых превышает 43, однако в данной статье они не приведены.

Отношение амплитуды главного лепестка к амплитуде боковых лепестков автокорреляционной функции (рисунок 3) позволяет проанализировать возможности полученных фазоманипулированных сигналов для различного числа дискретов. На рисунке 3 верхняя кривая определяет отношение амплитуд для уникальных сигналов, приведенных в таблице 2. Нижняя кривая на данном графике соответствует наиболее «неудачному» выбору кода фазоманипулированного сигнала (отношение амплитуд сигнала имеет наименьшее значение). Сопоставляя данные графики можно заметить, что разница между верхней и нижней кривыми составляет более 15 дБ. Средняя кривая (рисунок 3) получена для отношения амплитуд среднестатистического (выбранного на удачу) фазоманипулированного сигнала.

Отношение амплитуды (рисунок 4) главного лепестка к амплитуде боковых лепестков для значительно большего числа дискретов (до 300) подтверждает рост помехозащищенности фазоманипулированного сигнала с увеличением базы последнего, тем не менее разница между верхней и нижней кривыми практически постоянна и составляет около 15 дБ.

 

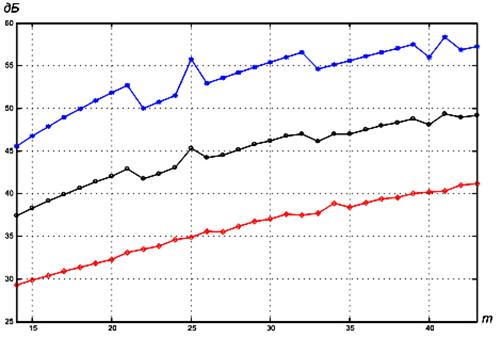
Рис. 3. Уровень боковых лепестков фазоманипулированных сигналов (число дискретов от 14 до 43).

 

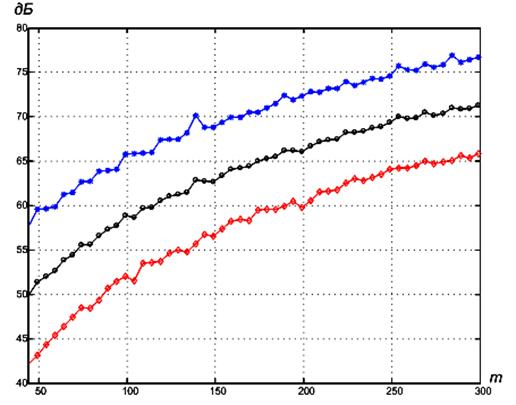
Рис. 4. Уровень боковых лепестков фазоманипулированных сигналов (число дискретов от 44 до 300).

 

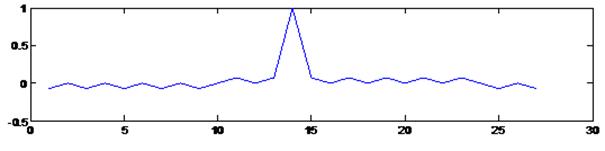
До сих пор, с помощью корреляционного анализа исследовались возможности сигналов разной длины с манипуляцией фазы, на основании свертки двух одинаковых сигналов. Однако при синтезе уникальных фазоманипулированных сигналов было установлено, что огибающая взаимной корреляционной функции двух разных последовательностей может быть приближена к желаемой форме (рисунок 5). Следует отметить, что свертка двух разных фазоманипулированных сигналов, один из которых излучается в пространство, а другой известен только корреляционному приемнику, значительно повышает скрытность и помехозащищенность системы обнаружения.

 

Рис. 5. Взаимная корреляционная функция двух разных фазоманипулированных сигналов и огибающие сигналов.

 

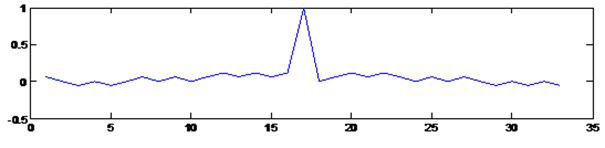
С помощью программного комплекса были найдены корреляционные функции с характерной огибающей (рисунок 6) для двух сигналов, один из которых является синусоидальным. При излучении обычного синусоидального сигнала с помощью корреляционного анализа могут быть получены огибающие функции неопределенности характерные для сложных сигналов.

 

Рис. 6. Взаимная корреляционная функция двух разных фазоманипулированных сигналов (один из которых периодичен) и огибающие сигналов.

 

Использование фазоманипулированных сигналов значительно повышает качественные и количественные показатели системы обнаружения.

Уникальные фазоманипулированные сигналы, которые были получены с помощью данного комплекса, могут быть применены во многих практических областях науки.

 

Литература.

 

1.                  Малеев А.В., Михайленко Я.В. Трехмерный акустический мультисенсорный мониторинг в задаче обнаружения и классификации подвижных объектов. – М.: РТСофт, «Мир компьютерной автоматизации» №2-2006.

2.                  Свистов В.М. Радиолокационные сигналы и их обработка. М., «Сов. Радио», 1977.

3.                  Яричин Е.М., Малеев А.В. Интеллектуальный акустический мониторинг реального времени в среде MATLAB. Транспортные средства Сибири: Межвуз. сб. науч. тр. с междун. уч. Вып. 10 / Под ред. С. П. Ереско. Красноярск: ИПЦ КГТУ, 2004.

4.                  Barker R. H. Group Synchronization of Binary Digital Systems. In: Communication Theory (W. Jackson, Ed.). Academic Press, New York, 1953.

5.                  Turyn R. On Barker Codes of Even Length. Proc. IRE, 1963, v.51, p. 1256.

 

Поступила в редакцию 07.08.2008 г.