Математическое моделирование движения жгута пищевой массы после горизонтального прессования.

 

Благовещенская Маргарита Михайловна,

доктор технических наук, профессор,

Иванов Яков Викторович,

аспирант

Московский Государственный Университет Пищевых Производств.

 

Большое количество теоретических работ посвящено математическому моделированию течения пищевых масс в каналах различной формы. Но после формования в прессе или в экструдере пищевая масса выходит из матричного отверстия и движется в воздухе в виде жгута.

При вертикальном прессовании траектория движения жгута однозначна: вертикально сверху вниз. Но теоретическое описание траектории жгута при горизонтальном прессовании, к сожалению, отсутствует, что затрудняет математическое моделирование процессов формования пищевых масс в кондитерской, хлебопекарной, макаронной и мясной промышленности.

Для построения математической модели рассмотрим движение жгута пищевой массы, выходящего из матричного отверстия с постоянной горизонтальной скоростью v_m. Большинство пищевых масс, помимо вязкости, обладают свойством ползучести [1], при которой скорость деформации под действием приложенной постоянной силы развивается во времени постепенно, достигая постоянной величины. Можно предположить, что не только вязкость, но и ползучесть будет влиять на траекторию жгута. Тогда исходное уравнение движения пищевой массы [2] с учетом ползучести будет иметь следующий вид:

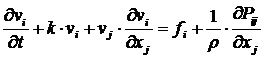,                                                              (1)

где i, j – индексы, принимающие значения 1, 2, 3;

t – время, с;

v_i – компоненты скорости смещения частицы пищевой массы, м/с;

x_i – оси координат, м;

k = G/η  ;

G – модуль сдвига при ползучести, Н/м²;

η – вязкость пищевой массы, Па;

f_i – компоненты напряженности массовых сил, м/с²;

ρ – плотность пищевой массы, кг/м³;

P_ij – тензор напряжений, Н/м².

Жгут, выходящий из формующего отверстия, состоит из однородной вязкой пищевой массы (конфетной, макаронной), поэтому тензор напряжений P_ij можно записать в виде 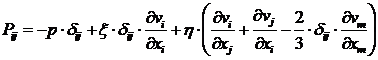[2]:

 ,                                 (2)    

где p – гидростатическое давление, Н/м²;

δ_ij – символ Кронекера;

ξ – объемная вязкость, Па;

∂v_m/∂x_m  − дивергенция вектора скорости смещения частицы пищевой массы, 1/с.

Жгут пищевой массы, вышедший из матричного отверстия, имеет свободные границы и внутри него отсутствует гидростатическое давление, не происходит резкое объемное сжатие или расширение, что позволяет считать пищевую массу несжимаемой. Следовательно, слагаемыми, содержащими символ Кронекера, можно пренебречь.  

Движение жгута пищевой массы происходит в плоскости, образованной вектором скорости выхода жгута из матричного отверстия и направлением ускорения свободного падения. Поэтому для того, чтобы записать компоненты уравнений (1) и (2), достаточно выбрать прямоугольную систему координат (горизонтальная ось x параллельна скорости выхода жгута, вертикальная ось  y направлена параллельно ускорению свободного падения) таким образом, чтобы середина матричного отверстия находилась на высоте y = h при x = 0. Тогда v_x(0,h) = v_m и v_y(0,h) = 0, так как в момент выхода жгута из матричного отверстия вертикальная составляющая скорости жгута отсутствует. Вне выбранной плоскости никакие силы не действуют, поэтому движением жгута в этом направлении можно пренебречь, так как деформация жгута происходит под действием вертикального ускорения свободного падения g.

Подобная задача решена в гидравлике для струи воды, истекающей из отверстия в вертикальной стенке. Уравнение траектории струи воды в выбранной системе координат имеет параболический характер:

 .                                                                                                       

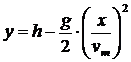С учетом принятых допущений из выражения (1) получаем соотношения для компонент скорости:

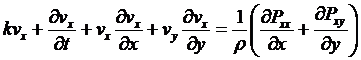,                                      (3)

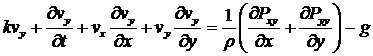,                                               (4)

а из выражения (2) получаем соотношения для ненулевых компонент тензора напряжения:

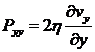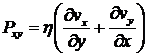; ; .                                       (5)

Из уравнения неразрывности получаем:

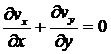 или .                                                                             (6)

Внутри жгута со свободными границами не могут образоваться вихревые течения, тогда

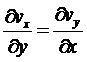 или .                                                                                   (7)

С учетом этих соотношений получаем, что

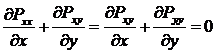.                                                                          (8)

При безвихревом плоском течении траекторию движения частицы пищевой массы, находящейся в центре поперечного сечения жгута, можно представить в виде линии тока [1]. Абсолютное значение скорости этой частицы не изменяется и равно v_m, но под действием ускорения g происходит поворот линии тока и изменение компонент скорости v_x и v_y, что позволяет записать:

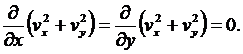 или                      (9)

Из соотношения (9) получаем:

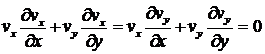.                                                              (10)

Тогда из уравнений (3) и (4) с учетом соотношений (6)-(10), получаем уравнения линии тока, проходящей через центр жгута пищевой массы:

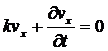 и 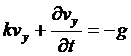,                                                                 (11)

решение которых можно записать в виде

 и .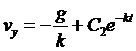

В момент времени t = 0 жгут пищевой массы начинает выходить из матричного отверстия со скоростью v_x = v_m при v_y = 0. Из этих условий находим константы интегрирования:

 и .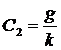

Тогда можно записать:

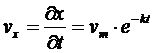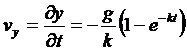  и                                         (12)

Интегрируя по времени выражения (12), соответственно получаем:

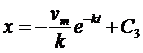 и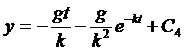                                               

Из начальных условий t = 0 , х(0) = 0 и у(0) = h находим постоянные интегрирования

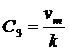  и ,

подставляя которые получаем

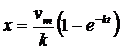 и 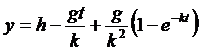.                                            (13)

Как видно из соотношений (13) при t → ∞, предельное значение х_п = v_m/k, а у стремится к отрицательному бесконечному значению.

Выражая t  через х и подставляя это значение t в равенство для у, получаем уравнение линии тока, а следовательно, и уравнение траектории жгута вязкой пищевой массы, обладающей ползучестью:

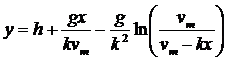.                                                                        (14)

Уравнение (13) позволяет математически моделировать движение жгута пищевой массы, обладающей ползучестью, после горизонтального прессования.

В случае отсутствия свойства ползучести у пищевой массы (k = 0) из уравнений (11) таким же путем получаем, что траектория движения жгута в этом случае будет параболической, как и у струи воды. 

На рисунке 1 приведены для сравнения результаты математического моделирования в системе компьютерной алгебры Maple движения жгута пищевой массы без учета ползучести f1(x) и с учетом ползучести f2(x).

 

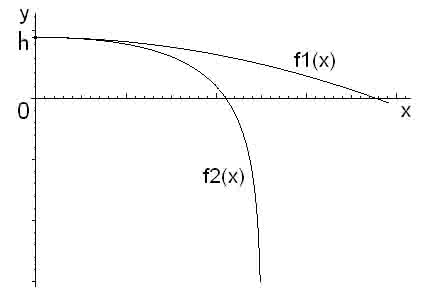
Рис. 1.

Траектории движения жгута пищевой массы.

 

Литература.

 

1. Мейз Дж. Теория и задачи механики сплошных сред. – М.: Изд-во ЛКИ, 2007. – 320 с.

2. Черняк В.Г., Суетин П.Е. Механика сплошных сред. – М.: ФИЗМАТЛИТ, 2006. – 352 с.

 

Поступила в редакцию 22.05.2008 г.