Волновые движения в основании с учётом
свойств, характерных для грунтовых и пористых сред
Давыдов
Александр Владимирович,
аспирант Московского государственного университета
приборостроения и информатики,
научный сотрудник НИЦ ОАО «Метрогипротранс».
Рассмотрено необратимое деформирование дилатантного
основания при ударном воздействии. Для материала основания использовалась
модель пластического упрочнения грунтов, позволяющая учесть такие общие
свойства для нескальных грунтов и пористых материалов, как нелинейность связи
между напряжениями и деформациями, зависимость значений достигнутых деформаций
от истории нагружения, зависимость объёмных и сдвиговых деформаций от первого и
второго инвариантов тензора напряжений, в частности явление дилатансии.
Приведены уравнения распространения возмущений и проведены численные расчёты.
Ключевые слова: дилатансия, необратимые
деформации, грунтовая среда, пористая среда.
Рассмотрим нормальное ударное воздействие тела
цилиндрической круглой формы на основание, для описания
материала которого применяется модель пластического упрочнения грунтов [1].
Считаем, что ось z
направлена вертикально вверх против направления скорости удара и является осью
симметрии, начало отсчёта z
от тыльной поверхности основания, ось r
ему ортогональна. В качестве определяющих соотношений для описания
упруго-пластического поведения материалов ударника и основания применялись
соотношения теории пластичности [4].
За условие пластичности примем обобщённое
условие Мизеса-Шлейхера, которое в пространстве
деформаций имеет следующий вид:
(1)
где 
и 
- компоненты девиаторов тензоров полных и пластических деформаций;
- компоненты тензора полных деформаций;
- компоненты тензора пластических деформаций;
- полная объёмная деформация;
- пластическая объёмная деформация;
- символ Кронекера;
F – заданная
функция от полных и необратимых деформаций;
G – модуль
сдвига;
К – коэффициент объёмного
расширения-сжатия.
Для материала основания функция F задаётся в виде [1]:
, (2)
где 
- функции параметров
упрочнения: 
и 
;
; 
, 
,
b – экспериментальная
постоянная, определяемая сцеплением и внутренним трением [1].
Для проведения численных экспериментов для
нескальных грунтов использовался модельный континуум [1], для которого функции 
принимают вид [6]:
,
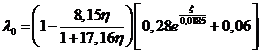, (3)
.
Для ударника 
(ударник выполнен из
идеально-пластического материала), 
- предел текучести.
Динамический процесс нестационарного
упруго-пластического поведения системы ударник-основание описывается следующей
системой десяти дифференциальных уравнений относительно десяти неизвестных
функций 
, 
, 
, 
, 
, 
, 
, 
, 
, 
[5] при условии, что
упругие свойства не зависят от пластических деформаций:
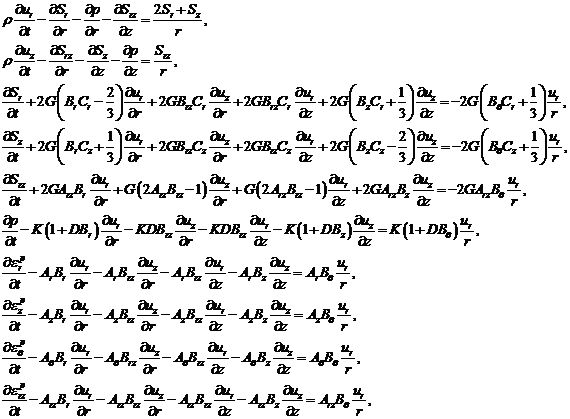(4)
где
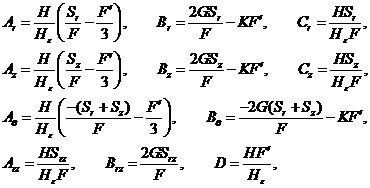
- плотность среды;
,
, 
, 
, 
,
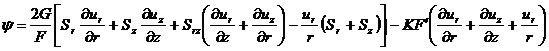
где p - первый инвариант тензора напряжений
(давление),
, 
, 
, - компоненты девиатора тензора напряжений:
.
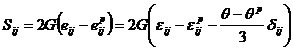Функция упрочнения 
имеет вид:
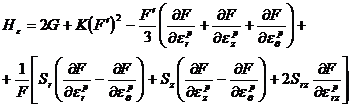(5)
Для рассматриваемого осесимметричного
случая введем следующие обозначения в
плоскости симметрии: V1 -область ударника с границей S1ÈS2, S1 –свободная от усилий граница, S2 - контактная граница ударника и основания; V2 -область,
занятая основанием с границей S3 - свободной от усилий.
В качестве начальных условий для системы (4) принимается:
при 
,
где 
- область, занятая
ударником и основанием,
- начальная скорость
удара.
Граничные условия:
где 
внизу обозначает
проекцию на нормаль, 
- проекцию на
направление касательной к границе, на которой ставятся граничные условия.
Квадратные скобки обозначают скачок заключённой в них величины.
Были проведены разнообразные численные
эксперименты для различных вариантов ударного взаимодействия. Система уравнений
(4) численно интегрировалась методом конечных элементов.
При расчётах использовалось обезразмеривание переменных: r1=r/R, z1=z/Z, где R – радиус основания, Z – сумма высот ударника и основания.
Рассматривался материал основания со
следующими характеристиками: плотность = 2720 кг/м3, модуль сдвига G
= 9,3 МПа, коэффициент объемного расширения-сжатия K = 27,8 МПа, величина b
= 0,16 МПа. Материал ударника имеет следующие деформационные и прочностные
характеристики: плотность = 2700 кг/м3, модуль сдвига G
= 26,2 ГПа, коэффициент объемного расширения-сжатия K = 63,6 ГПа, начальный
предел текучести =0,37 ГПа.
Численные эксперименты были проведены для
двух случаев скорости удара, безразмерной по отношению к скорости упругих волн:
1) 0.02; 2) 0.04.
В каждом случае графики функций выводились для 10 моментов времени: 1 –
t=0.3 мкс, 2 – t=0.6 мкс, 3 – t=0.9 мкс, 4 – t=1.2 мкс, 5 – t=1.5 мкс, 6 – t=1.8 мкс, 7 – t=2.1 мкс, 8 – t=2.4 мкс, 9 – t=2.7 мкс, 10 – t=3.0 мкс
На рис. 1-2 приведены графики для
интенсивности пластических деформаций сдвига 
, пластической объёмной деформации 
вдоль контактной
границы основания и ударника для первого случая, а на рис. 3-4 приведены
графики соответственно для второго случая.
Сравнение результатов расчётов показывает, что максимальные значения
интенсивности пластических деформаций сдвига и объёмной пластической деформации
на контактной границе основания и ударника во втором случае больше на 60%. Вдоль
контактной поверхности величины и в обоих случаях меняются
незначительно. Положительность объёмной пластической деформации свидетельствует
о том, что происходит пластическое уплотнение материала под ударником. Данную
модель можно использовать для исследования напряжённо-деформированного
состояния грунтовых и пористых сред при различных условиях динамического нагружения.
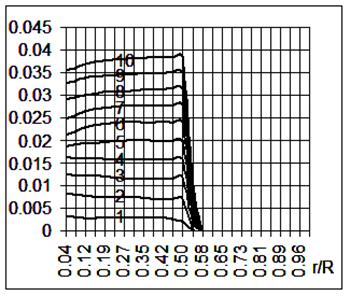
Рис.1. Интенсивность пластических
деформаций сдвига (1 случай).
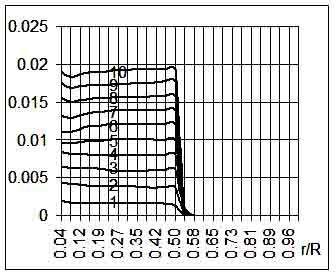
Рис. 2.
Объёмная пластическая деформация 
(1 случай).
Рис.3.
Интенсивность пластических деформаций сдвига (2 случай).
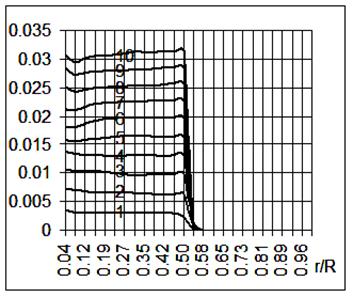
Рис. 4.
Объёмная пластическая деформация 
(2 случай).
Литература
1. Григорян С.С., Зуев В.В., Иоселевич В.А. О
закономерностях пластического упрочнения грунтов. IV Всесоюзный съезд по теоретической и
прикладной механике. Аннотации
докладов. – Киев, 1976. – С. 89.
2. Давыдов А.В., Зуев В.В. О динамическом нагружении дилатантных сред. Смешанные
задачи механики деформируемого тела. Материалы V Российской конференции с
международным участием. Саратовский государственный университет. – Саратов, 2005. – С.265.
3. Давыдов А.В., Зуев В.В. Поведение
уплотняющихся материалов при ударных нагружениях. Обозрение прикладной и промышленной
математики. 2007. Т14. Вып.3. С.531.
4. Зуев В.В. Определяющие соотношения и
динамические задачи для упруго-пластических сред с усложнёнными
свойствами. – М: ФМ, 2006. – 174 с.
5. Зуев В.В., Шмелёва А.Г. Осесимметричное ударное нагружение упруго-пластической среды с разупрочнением и
переменными упругими свойствами. Вестник СамГУ.
Естественнонаучная серия. 2007. №2(52). С.100-106.
6. Иоселевич В.А. Об эффектах пластического
упрочнения нескальных грунтов. Научные труды Института механики МГУ. – М.:МГУ,
1975. - №42. – С.96-112.
Поступила в редакцию 15.07.2008
г.
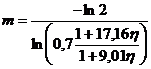