Применение метода конформного преобразования к одной задаче в криволинейном четырехугольнике для  распространения  тепла.

 

Рагимова Кямаля Разим,

соискатель Бакинского Государственного Университета.

 

Рассматривается распространение тепла в теле, неограниченном в направлении, перпендикулярном к плоскости , в котором вектор теплового потока в каждой точке параллелен плоскости . Поэтому эта задача с установившейся температурой формулируется не для самого тела, а для его сечения, перпендикулярного к плоскости :

                                           (1)

                                                                      (2)

где  четырехугольник, ограниченный дугами двух софокусных эллипсов и двух гипербол; граница области , в форме криволинейного четырехугольника состоящего из частей, уравнения которых имеют вид:

  

 

соответственно,

Проводится конформное преобразование

Тогда

и

                

Следовательно, контур  в результате такого преобразования переходит в  контур прямоугольника на плоскости

При этом конформном преобразовании  и  являются сопряженными гармоническими функциями  и . Следовательно

Отсюда вытекает, что кривые  и  ортогональны. Кроме того, поскольку  и  то   и, аналогично  Далее, если является такой функцией   и , что

то можно показать, что

Так 

,

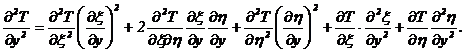
Складывая, эти два выражения и используя вышеприведенные соотношения, получим

Итак, если мы можем получить решение уравнения

                                                                   (3)

удовлетворяющее граничному условию:

                                                                           (4)

то это решение на плоскости  можно преобразовать в решение на плоскости .

Решение задачи (3), (4) получается разбиением ее на четыре случая, в каждом из которых три границы поддерживаются при нулевой температуре. Граничные условия для первой из этих четырех задач запишутся таким образом:

             при                                       (5)

 при                                       (6)

 при                                        (7)

 при                                        (8)

Запишем  в виде ряда по синусам

где

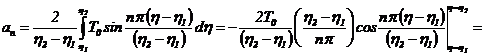
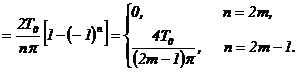
Для любого  член вида

удовлетворяет соотношениям (3), (6), (7) и (8). Теперь рассмотрим выражение

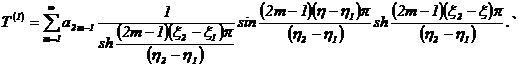(9)

Далее, так как

               

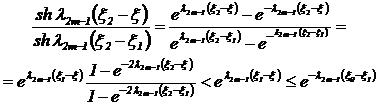
при      а ряд   

сходится, и его члены не зависят от  и

Таким образом, ряд (9), рассматриваемый как функция , равномерно сходится в любом интервале , когда . Если же его рассматривать как функцию , то он равномерно сходится при

В этих интервалах сходится также ряды, получаемые из ряда (9) почленным дифференцированием по  и .

Действительно,

и при  ряд    сходится.

Следовательно,

и ряд (9) удовлетворяет дифференциальному  уравнению (3). Кроме того, он удовлетворяет условиям (5)-(8); это проверяется непосредственными подстановками под знаком суммы,  благодаря  равномерной сходимости ряда (9) в соответствующих интервалах.

Граничные условия для второй из этих четырех задач имеют вид:

   при   

 при  

   при     

  при       

и решение второй задачи получается аналогичным образом:

.

Граничные условия для третьей и четвертой задачи выглядят следующим образом:

  при           при      

  при         при  

  при   ,       при   ,

  при   ,       при   ,

соответственно и решения этих задач имеют вид:

  

Таким образом, решение задачи (3), (4) получаем в виде:

 

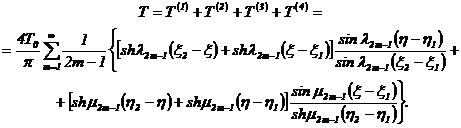
Литература.

 

1.                  М.А.Лаврентьев, Б.В.Шабат. Методы теории функции комплексного переменного. Москва, 1965

2.                  Г.Карслоу и Д. Егер. Теплопровдность твердых тел, Москва, 1964.

3.                  Г.Джеффрис, Б.Свирлс. Методы математической физики, т.2, М., 1970.

 

Поступила в редакцию 14.02.2008 г.