Экспериментальное исследование кодека АДИКМ при передаче сигналов данных с QAM-модуляцией

Никитин Дмитрий Александрович,

аспирант,

Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М.А. Бонч-Бруевича.

Несмотря на то, что телефонная сеть общего пользования рассчитана, в первую очередь, на передачу речевых сигналов, часто телефонные каналы используются и для передачи данных, поэтому иногда к речевым кодекам предъявляется требование прозрачности для неречевых сигналов. Не все методы кодирования речи обеспечивают более или менее приемлемую передачу модемных сигналов. В наибольшей степени этому требованию отвечают методы временного кодирования (кодирования формы сигнала). Наиболее широко используемыми методами кодирования формы являются импульсно-кодовая модуляция с компрессией динамического диапазона и адаптивная дифференциальная импульсно-кодовая модуляция (АДИКМ).

Метод АДИКМ является одним из наиболее эффективных методов временного кодирования речевых сигналов. Выигрыш в скорости достигается за счет того, что квантованию, кодированию и последующей передаче по каналу связи подвергается разность между истинным и предсказанным значениями входного сигнала – сигнал ошибки предсказа­ния [1]. Так как отсчеты речевого сигнала при частоте дискретизации 8 кГц сильно коррелированны, дисперсия сигнала ошибки предсказания оказывается существенно меньше дисперсии входного сигнала, и для ее кодирования используется меньшее число битов. Отсчеты сигнала передачи данных обладают гораздо более слабой корреляцией, поэтому метод АДИКМ существенно менее эффективен для передачи сигналов модемов.

Алгоритм адаптивной дифференциальной импульсно-кодовой модуляции стандартизован в рек. МСЭ-Т G.726. При разработке данной рекомендации учитывалась необходимость передачи наряду с речевыми сигналами и сигналов модемов.

Начиная с 80-х годов XX века проводились исследования, призванные оценить возможности различных разрабатывавшихся в то время алгоритмов АДИКМ по передаче сигналов данных [2]. Некоторые результаты приведены в документе МСЭ-Т [3], где подчеркивается, что сделанные заключения являются предварительными. Также следует отметить, что значительная часть исследований носит экспериментальный характер, а полученные результаты различаются для разных типов исследуемых модемов.

Таким образом, задачу оценки степени «прозрачности» речевых кодеков для неречевых сигналов нельзя считать полностью решенной. Наряду с рек. G.726 существуют и друге варианты построения кодеков АДИКМ. В частности, известна структура предсказателя, построенная с позиций теории оптимального оценивания [4].

При передаче данных по телефонному каналу с АДИКМ-кодеком система состоит из оконечного оборудования данных (ООД) передачи, модулятора, кодера АДИКМ, идеального цифрового канала, декодера АДИКМ, демодулятора и ООД приема [5].

При кодировании методом АДИКМ возникает задача предсказания текущего значения сигнала по некоторой комбинации предыдущих значений. Существуют различные методы решения данной задачи, однако из всех линейных алгоритмов экстраполяции наилучшим по критерию минимума среднего квадрата ошибки предсказания является алгоритм Калмана–Бьюси. На его основе получена модифицированная структура адаптивного экстраполято­ра, пригодного для использования в кодеках АДИКМ [6]. Его исследование позволяет определить потенциальные возможности кодеков АДИКМ для передачи неречевых сигналов.

Мерой точности предсказания является энергетический выигрыш g, представляющий собой отношение среднеквадратических значений кодируемого QAM-сигнала (входного сигнала кодера) и сигнала ошибки предсказания. Представляет интерес исследование влияния на энергетический выигрыш следующих параметров экстраполятора:

– порядка;

– значений коэффициентов адаптации;

– числа точек в сигнальном созвездии QAM-сигнала;

– наличия/отсутствия рекурсивной части.

Для нахождения указанных зависимостей было произведено компьютерное моделиро­вание кодера АДИКМ с оптимальным одношаговым экстраполятором. Моделирование производилось при следующих исходных данных:

– единичный элемент сигнала: sinx/x, взвешенный окном Хэмминга;

– скорость следования двумерных символов 3100 Бод;

– несущая частота 1850 Гц;

– частота дискретизации 8 кГц;

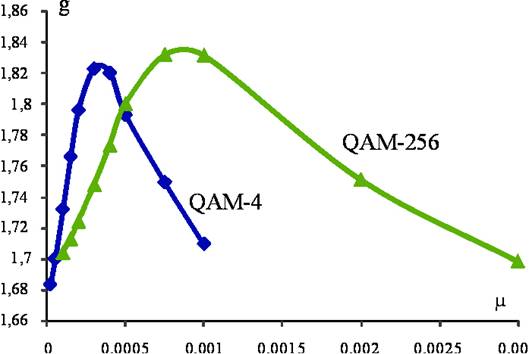
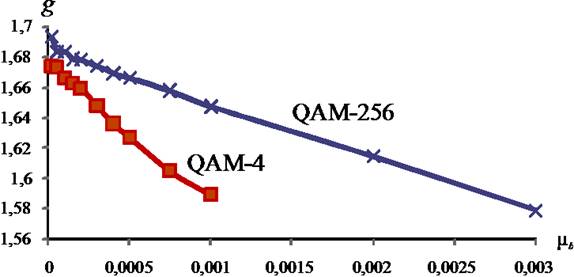
Полученные зависимости энергетического выигрыша от значения коэффициента адаптации для разного числа точек в сигнальном созвездии приведены на рис. 1.

а)

б)

Рис. 1. Зависимость энергетического выигрыша от коэффициента адаптации
при различном числе точек в сигнальном созвездии
a) – предсказатель рекурсивного типа; б)  – предсказатель нерекурсивного типа.

Важнейшей характеристикой алгоритма АДИКМ является порядок фильтра-предсказателя. На рис. 2 приведены кривые энергетического выигрыша, полученные при использовании предсказателей различного порядка.

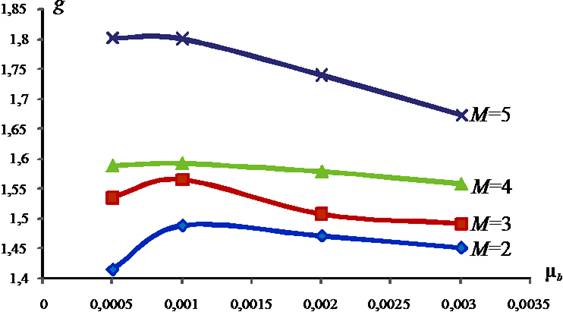
Рис. 2. Зависимость энергетического выигрыша от коэффициента адаптации
при различном порядке фильтра-предсказателя.

Для практических целей наибольший интерес представляет оценка достижимой вероятности ошибки QAM-сигнала при передаче данных по каналу, оборудованному АДИКМ-кодеком. В [5] получено следующее выражение для помехозащищенности QAM-сигнала:

,

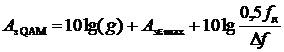где A_{зε max} – максимально достижимая помехозащищенность квантуемого разностного сигнала по шумам квантования и ограничения; f_д = 8 кГц – частота дискретизации, Δf = 3,1 кГц – ширина эффективно передаваемой полосы частот канала ТЧ.

Как известно, шум квантования распределен по равномерному закону. Однако на приеме осуществляется когерентное детектирование и фильтрация сигналов синусного и косинусного подканалов, а линейная система (фильтр приема) нормализует закон распределения. Поэтому шум квантования на входе решающей схемы можно приближенно считать нормальным. Следовательно, задача сводится к определению вероятности ошибки QAM-сигнала при воздействии аддитивного гауссовского шума. Решение этой задачи хорошо известно [4].

В таблице 1 приведены значения вероятности ошибки для различного числа точек в сигнальном созвездии и различного числа бит в кодовом слове.

Таблица 1.

Вероятности ошибки

для различного числа точек в сигнальном созвездии и различного числа бит в кодовом слове.

При использовании для передачи данных сигнала QAM-4 (M=2) связь возможна при любых значениях числа бит в кодовом слове, кроме m=2. Символы QAM-16 (M=4) могут использоваться только при скоростях цифрового потока АДИКМ-кодера, равных 40 и 32 кбит/с. Использование двумерных символов с большим числом состояний (QAM-64 и выше) становится невозможным из-за катастрофического возрастания вероятности ошибки. Если для кодирования аналогового сигнала в канале используется кодер АДИКМ-16 (m=2), то метод квадратурной амплитудной модуляции для передачи данных по такому каналу неприменим.

Таким образом, энергетический выигрыш в наилучшем случае составляет величину порядка 1,8, что приводит к увеличению помехозащищенности по шумам квантования на 2,6 дБ по сравнению с квантованием самого сигнала с тем же числом битов в кодовом слове.

Литература

1.                  Шелухин, О.И. Цифровая обработка и передача речи / О.И. Шелухин, Н.Ф. Лукьянцев. – М.: Радио и связь, 2000.

2.                  Evaluation of ADPCM coders for digital circuit multiplication equipment / S. Dimolitsas, F.L. Corcoran, M. Onufry, H.G. Suyderhoud // COMSAT Technical Review. – Fall 1987. – Vol. 17(2). – p. 325–345.

3.                  ITU Rec. G.726 Appendix III. Comparison of ADPCM algorithms. – Geneva, 1994.

4.                  Курицын, С.А. Основы построения телекоммуникационных систем передачи: учебное пособие / С.А. Курицын. – СПб: Выбор, 2004.

5.                  Никитин, Д.А. Оценка вероятности ошибки QAM-сигнала передачи данных при кодировании методом АДИКМ / Д.А. Никитин // Труды учебных заведений связи / ГОУВПО СПбГУТ. – СПб, 2007. – № 177.

6.                   Никитин, Д.А. Оценка эффективности оптимальной экстраполяции сигнала QAM / Д.А. Никитин // Труды учебных заведений связи / ГОУВПО СПбГУТ. – СПб, 2008. – № 178.

Поступила в редакцию 17.07.2008 г.