Соотношения параметров модели Гилберта и  простой Марковской цепи

 

Мелентьев Олег Геннадьевич,

доктор технических наук, доцент,

Шевнина Ирина Евгеньевна,

старший преподаватель.

Сибирский государственный университет телекоммуникаций и информатики.

 

В реальных каналах связи ошибки, возникающие при приеме единичных элементов, а так же поражения блоков имеют тенденцию к группированию. Для описания статистики ошибок в таких каналах часто используют простую Марковскую цепь с двумя состояниями или модель Гилберта [1-3]. Простая цепь задается матрицей переходных вероятностей 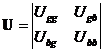. Физический смысл элементов матрицы – вероятность принять следующий элемент без ошибки (с ошибкой) если текущий принят без ошибки (с ошибкой). В модели Гилберта простой цепью и, следовательно, матрицей переходных вероятностей описывается процесс смены состояний канала. Одно состояние является хорошим (S_g), в нем ошибок нет. Второе состояние (S_b) – плохое, с вероятностью возникновения ошибок . Матрицу переходных вероятностей модели Гилберта обозначим следующим образом 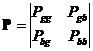 . Финальные вероятности состояний определяются известными формулами [3]:

;          .

Применение простой цепи в качестве модели канала упрощает процессы статистической оценки параметров канала и последующего анализа, но возможности данной модели не всегда позволяют удовлетворительно описать все характеристики канала с группированием ошибок. В таких случаях целесообразно перейти к модели Гилберта.

Модель Гилберта всегда может быть преобразована в простую цепь, используя приведенные ниже выражения

;                                                                                           (1)

;                             (2)

;                                                                                                             (3)

.                                                              (4)

Обратный переход имеет множество решений. Определим основные свойства семейства моделей Гилберта, соответствующих заданной простой цепи. Исходную простую цепь далее будем называть порождающей, а соответствующие ей модели восстановленными.

Для восстановления необходимо задать вероятность возникновения ошибок в плохом состоянии . Тогда из выражения (3)  получим вероятность сохранения плохого состояния

.                                                                                                               (5)

Из выражений (1) и (5), следует 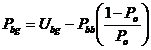                                    (6)

Преобразуем выражение (4), используя известное соотношение :

.

Получим соотношение .

Введем обозначение  и выразим финальную вероятность через переходные вероятности:

;

;

;

.

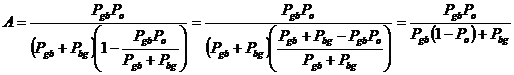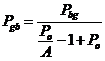Подставляя значение А, получим

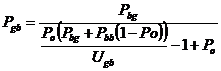.                                                                         (7)

Из свойства стохастичности найдем

.                                                                                                             (8)

Одним из очевидных общих свойств всех восстановленных моделей является равенство среднего коэффициента ошибок .

Выразим из выражения (7) вероятность , через вероятности порождающей цепи

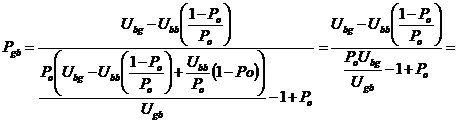
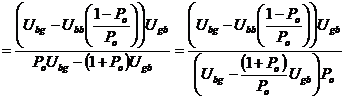.                                          (9)

Определим средние длины плохого и хорошего состояний:

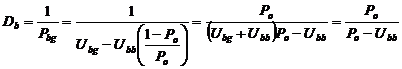;                            (10)

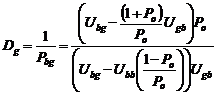.                                                                           (11)

Найдем отношение средних длин хорошего и плохого состояний для всего семейства восстановленных моделей при разных вероятностях ошибки в плохом состоянии:

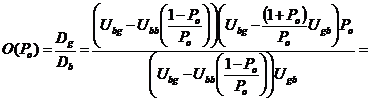
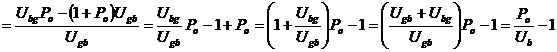
Нетрудно доказать, что

,

где ( ) – средние длины безошибочных серий и серий ошибок, соответствующие порождающей цепи.

Таким образом, для отношения средних длин можно записать

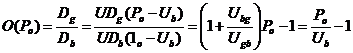.                                        (12)

Анализируя полученный результат, можно сформулировать следующее свойство – отношение средних длин состояний будет линейно зависеть от вероятности ошибки в диапазоне  (рис. 1). При , отношение будет максимальным и равным отношению средних длин порождающей цепи .

 

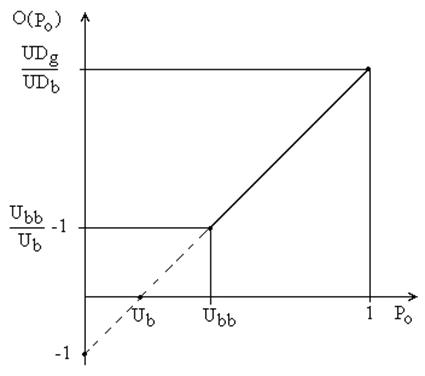
Рис. 1.

Зависимость отношения средних длин состояний для семейства восстановленных моделей Гилберта от вероятности ошибки в плохом состоянии и параметров порождающей цепи.

 

При , как следует из выражения (5), вероятность  становится равной единице, т.е. цепь становится поглощающей, что не соответствует модели Гилберта.

 

Из рассмотренных свойств следуют соотношения:

–  вероятности плохого и хорошего состояний    , ;

– отношение финальных вероятностей имеет ту же зависимость, что и отношение средних длин    ;

– длина хорошего состояния 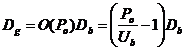     ;                            (13)

– цикл модели Гилберта равен    ;

– отношение длины цикла к среднему числу ошибок в цикле постоянно и равно коэффициенту наклона прямой:

;

Коэффициент группирования

.

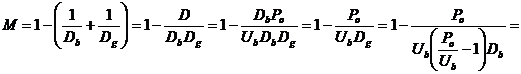
На рисунке 2 приведены типовые зависимости средних длин состояний и коэффициента группирования от вероятности ошибки в плохом состоянии для моделей Гилберта восстановленных из Марковской цепи, заданной переходными вероятностями  и .

 

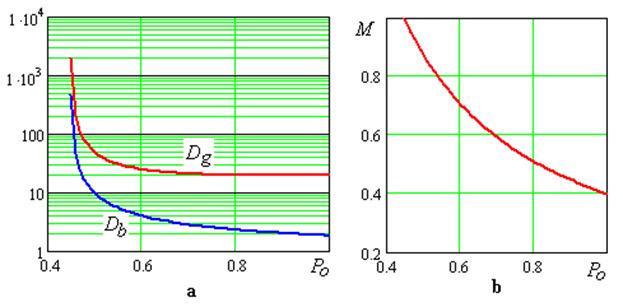
Рис. 2.

Зависимости средних длин состояний (a) и коэффициента группирования (b) от вероятности ошибки в плохом состоянии.

 

Полученные соотношения позволяют однозначно восстановить параметры модели Гилберта из простой цепи Маркова при минимуме дополнительной информации. В качестве дополнительной информации можно использовать один из параметров модели Гилберта или статистически полученную точку, какой либо характеристики, например, характеристики распределения вероятностей кратных ошибок в блоке фиксированной длины или вероятность безошибочной серии заданной длины.

 

Литература.

 

1.       Мелентьев О.Г. Теоретические аспекты передачи данных по каналам с группирующимися ошибками /под редакцией профессора В.П. Шувалова  – М.: Горячая линия –Телеком, 2007. –253с.:ил.

2.       Zorzi M. and Rao R.R. Lateness Probability of a Retransmission Scheme for Error Control on a Two-State Markov Channel // IEEE Transactions on Communications, October, 1999.

3.       Hueda M. R., Rodriguez C. E. On the Relationship Between the Block Error and Channel-State Markov Models in Transmission Over Slow-Fading Channels // IEEE Transactions on Communications, August, 2004.

 

Поступила в редакцию 15.07.2008 г.