Идентификация случайных процессов на основе формирования их адаптивных моделей

Манохин Антон Евгеньевич,

аспирант кафедры радиоэлектронных и телекоммуникационных систем Уральского государственного технического университета – УПИ».

Необходимость разработки систем идентификации случайных процессов диктуется практикой, а их практическое применение актуально, например, в автоматических системах опознавания говорящего по голосу [1] или в криминалистике [2-4]. В этом случае в качестве идентифицируемого процесса выступает речевой сигнал, по сути являющийся случайным процессом [5].

В статье представлен алгоритм идентификации стационарных случайных процессов с априорно неизвестными характеристиками, основанный на формировании их моделей.

В основе данного алгоритма лежит работа адаптивного фильтра, который способен во времени подстраиваться под входной сигнал. Если на входе адаптивного фильтра кроме полезного сигнала действует белый шум, то последний возбуждает N-мерное пространство весовых коэффициентов [6]. В свою очередь, адаптивный фильтр на­страивается в соответствии с адаптивным алгоритмом (например, по методу наименьших квадратов - МНК) таким образом, чтобы его выходной сигнал соответ­ствовал неизвестному сигналу в общем случае по критерию наилучшего среднеквадратического приближения. Т.е., адаптивная система настраивается на неизвестный сигнал и становится его моделью [7].

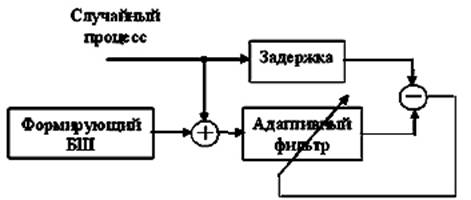
Рис. 1. Структурная схема формирователя модели случайного процесса.

Структурная схема формирователя модели представляет собой адаптивный трансверсальный фильтр, на входе которого действует смесь идентифицируемого случайного процесса и формирующего «белого шума» (рис.1).

В ходе минимизации среднеквадратического значения или средней мощности сигнала ошибки адаптивный фильтр подавляет действующий на его входе «белый шум» и выделяет идентифицируемый сигнал. Таким образом, импульсная характеристика адаптивного трансверсального фильтра будет стремиться к соответствию с идентифицируемым сигналом и указывать на определенный случайный процесс.

Имея в распоряжении библиотеку различных импульсных характерис­тик адаптивных фильтров, соответствующих случайным процессам с известными параметрами, имеется возможность сравнивать с ней импульсную характеристику, соответствующую идентифицируемому случайному процессу [8].

Выбор критерия идентификации заключается в нахождении такого способа, который может успешно и эффективно провести сравнение исследуемого случайного процесса с имеющейся моделью. Такое сравнение можно проводить двумя способами (рис.2).

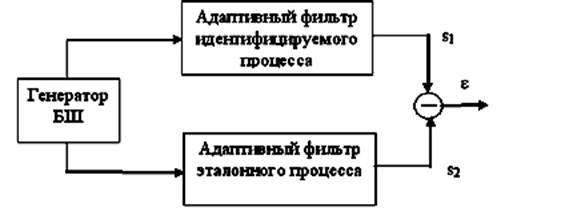
Рис. 2. Структурная схема устройства модельной идентификации случайных процессов.

Первый способ основан на сравнении инициализируемого сигнала с известным через дисперсию ошибки ε на выходе схемы вычитания, которая, по сути, является средним квадратом евклидового расстояния между сигналами. Очевидно, что если через фильтр с импульсной характеристикой, полученной в ходе формирования модели определенного случайного сигнала, пропустить выборку данных белого шума, то на выходе этого фильтра мы получим модель случайного сигнала. Ее параметры будут соответствовать тому случайному сигналу, который применялся для получения импульсной характеристики этого адаптивного фильтра. Тогда критерий идентификации можно записать:

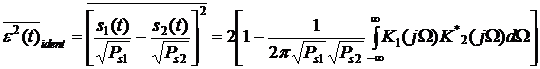(1)

где      K₁(jΩ) – коэффициент передачи адаптивного фильтра идентифицируемого процесса; K₂(jΩ) – коэффициент передачи адаптивного фильтра эталонного процесса; P_s1 и P_s2 – мощности моделей сравниваемых процессов; Ω – нормированная частота (к частоте дискретизации).

Второй способ вытекает из непос­редственного сравнения весовых коэффициентов исследуемых характе­ристик фильтров. Каждый весовой коэффици­ент адаптивного трансверсального фильтра сравнивается с соответс­твующим по порядковому номеру весовым коэффициентом второго адап­тивного фильтра. Результаты сравнения всех коэффициентов склады­ваются и затем усредняются по общему числу этих весовых коэффици­ентов, т.е.

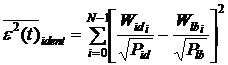,                                                                        (2)

где      W_id – весовые коэффициенты АФ идентифицируемого процесса; W_lb – весовые коэффициенты АФ эталонного процесса; P_id и P_lb определяется как .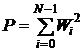

Покажем на примере марковского процесса, что критерии (1) и (2) при определенных допущениях могут давать одинаковый результат. Пусть эталонная модель марковского процесса имеет эффективную ширину полосы α₂, а исследуемый марковский процесс – α₁. Также примем допущение, что выбрано оптимальное отношение мощности моделируемого случайного процесса [9]. Тогда можно записать:

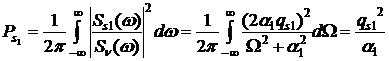
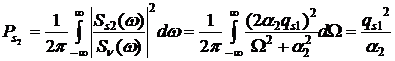
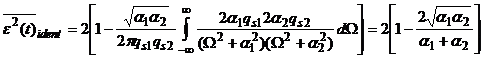         (3)

где q_s1 и q_s2 – отношение мощности случайного процесса (идентифицируемого и эталонного соответственно) к мощности формирующего белого шума.

Аналогично выполним вычисления для второго метода. Запишем оптимальный вектор весовых коэффициентов моделей идентифицируемого и эталонного процессов:

где k₁ и k₂ – нормированные корреляционные функции случайных процессов.

Тогда

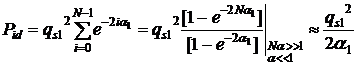
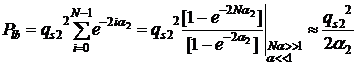
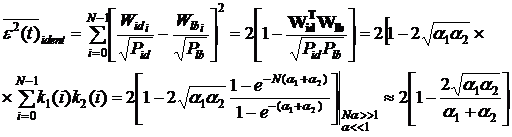(4)

Для того, чтобы сравнить дисперсию ошибки идентификации случайных процессов с разной шириной спектральной плотности мощности продифференцируем по α₁ выражение (4) и, подставив α₁=α₂-Δα, найдем крутизну:

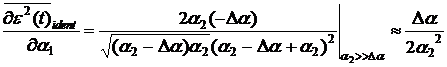                  (5)

Анализ формулы (5) позволяет сделать вывод, что идентификация проводится более точно, если имеется случайный процесс с более узкой полосой.

Было проведено практическое моделирование, где в качестве идентифицируемого сигнала выступал марковский процесс (с относительной шириной спектральной плотности эталонных моделей α₀₂=0.1 и α₀₁=0.01). Критериям правильной идентификации выступала дисперсия ошибки идентификации (ф.2), который при меньшей длине модели является более состоятельным, нежели критерий (1), требующий больших временных затрат на оценку.

В качестве изменяемых входных параметров адаптивных фильтров задавались: q=-10дБ, N=256, М =10^-3 (коэффициент расстройки).

Результаты моделирования изображены на рис.3.

Таким образом, представленный алгоритм идентификации случайных процессов на основе формирования их адаптивных моделей демонстрирует хорошую работоспособность, а анализ рис.3 показывает, что случайный процесс по дисперсии ошибки идентификации (ф.2) точнее идентифицируется, имея более узкую эффективную спектральную ширину, чем более широкополосный процесс.

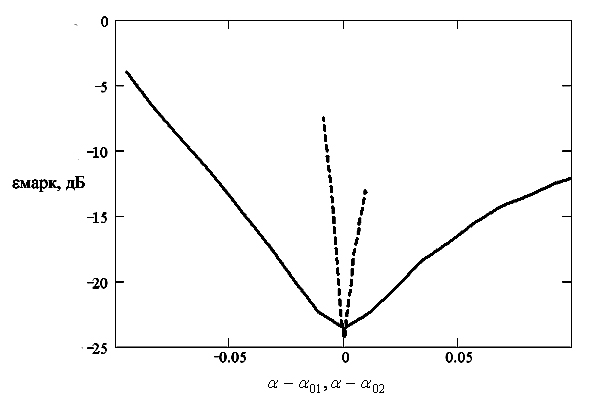
Рис. 3. Дисперсия ошибки идентификации для марковского процесса с α₀₂=0.1 (сплошная линий) и α₀₁=0.01 (пунктирная линия).

Литература.

1. Рамишвили Г. С. Автоматическое опознавание говорящего по голосу. М.: Радио и связь, 1981.

2. Идентификация человека по магнитной записи его речи (Методическое пособие для экспертов, следователей и судей). М.: РФЦСЭ при МЮ РФ, 1995. - 130 с.

3. Ложкевич А.А., Снетков В.А., Чиванов В.А., Шаршунский В.Л. Основы экспертного криминалистического исследования магнитных фонограмм. М.: ВНИИ МВД СССР, 1977. - 172 с.

4. Рамишвили Г.С., Чикоидзе Г.Б. Криминалистическое исследование фонограмм речи и идентификация личности говорящего. Тбилиси: «Мецниереба», 1991. - 265 с.

5. Маркел Дж., Грей А. X. Линейное предсказание речи / Пер. с англ. М.: Связь, 1980.

6. Neil J. Bershad, Jose Carlos M. Bermudes. “Sinusoidal interference rejection analysis of an LMS adaptive feedforward controller with a noisy periodic reference”. IEEE Transaction on signal processing, vol.46, N5, May 1998.

7. Манохин А.Е., Нифонтов Ю.А. О некоторых приложениях моделирования сигналов с использованием адаптивных фильтров // Радиолокация. Навигация. Связь. Труды десятой международной научно-технической конференции. Воронеж: изд. НПФ «Саквоее» ООО,2004. С.54.

8. Манохин А.Е., Нифонтов Ю.А. Идентификация случайных процессов с использованием их моделей. // Научные труды VI отчетной конференции молодых ученых ГОУ ВПО УГТУ-УПИ: Сборник статей. В 2 ч. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2004. Ч1. 445с.

9. Манохин А.Е., Нифонтов Ю.А. Применение адаптивного моделирования для формирования моделей сигналов. // Новые методы передачи и обработки информации: Сборник результатов научных исследований сотрудников радиотехнического факультета УГТУ-УПИ. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. 258с.

Поступила в редакцию 15.09.2008 г.