Прогнозирование времени ожидания сигнальных сообщений в буфере звена сигнализации  ОКС №7 с помощью нейронных сетей.

 

Лизнева Юлия Сергеевна,

старший преподаватель кафедры Автоматической Электросвязи  Сибирского Государственного Университета Телекоммуникаций и Информатики.

 

В настоящей работе рассматриваются проблемы, возникающие при расчете времени ожидания в очереди сигнальных сообщений в буфере звена сигнализации. Описывается нейросетевой метод прогнозирования времени ожидания в очереди сигнальных сообщений. Показано, что предлагаемая методика имеет преимущества для практического применения по сравнению с аналитическими методами расчета характеристик потоков сигнальных сообщений, передаваемых по звену ОКС №7.

 

Постановка задачи.

 

Эффективность работы телекоммуникационной сети зависит от способа построения и функционирования сети передачи сигнальной информации. Сеть общеканальной сигнализации должна обеспечивать гарантированную доставку сигнальной информации для различных подсистем  пользователей посредством сокращения времени доставки сообщений и защиты от искажений [1,7]. Оптимальность сети сигнализации определяется комплексом показателей качества ее функционирования, таких как интенсивность сигнальной нагрузки, обслуживаемой звеньями сигнализации, среднее время и дисперсия задержки сообщений в звене сигнализации [9].

Рассчитав и проанализировав для конкретной сети сигнализации значения задержки сообщений, можно оценить качество ее функционирования. Для расчета характеристик сети звено  сигнализации представляется в виде одноканальной модели системы массового обслуживания, на которую поступает поток сигнальных сообщений [5].

При расчете времени доставки сигнальных единиц в пределах одного звена сигнализации необходимо учитывать, что сообщение  на втором уровне ожидает обслуживания в буфере передачи некоторое время. При этом может образоваться очередь, тогда полное время доставки сообщения  определяется как сумма времени передачи сообщения и времени ожидания в очереди. Длительность передачи сигнальных единиц зависит от их длины и скорости передачи в канале, а для расчета времени ожидания сообщения в очереди требуется учет дисциплины обслуживания сигнальных единиц.

В ряде публикаций [2, 3] показано, что только поток сигнальных сообщений, поступающих от источников, не являются независимыми пуассоновскими.

Одноканальная система массового обслуживания, на вход которой поступает поток сигнальных сообщений с интенсивностью λ и произвольным распределением интервалов времени между поступлением и произвольным временем обслуживания соответствует системе массового обслуживания типа G/G/1.

Для расчета времени ожидания в очереди в системе массового обслуживания типа G/G/1 можно воспользоваться аналитическим выражением [5]:

,                                                                 (1)

где , - среднеквадратическое отклонение интервалов между поступлением сигнальных сообщений и времени обслуживания соответственно; - среднее значение интервала времени между поступлениями сигнальных сообщений; - интенсивность поступающей нагрузки на одно звено.

Сложность расчета времени ожидания сообщений в очереди с использованием выражения 1 заключается в том, что опирается на четыре взаимозависимые величины. Следовательно, точно рассчитать время ожидания в очереди, используя выражения 1, возможно только при наличии полной статистической информации о работе звена сигнализации.

Так как абсолютные значения величин с учетом их размерности не позволяют сравнивать процессы, зависящие от многих атрибутов, в работе ставится задача разработки методики, которая позволила бы перейти к относительным единицам.

Основным направлением для решения поставленной задачи может быть применение нейросетевых методов прогнозирования [4,8]. У данного метода прогнозирования можно выделить ряд преимуществ:

·                    отсутствие формальной модели;

·                    быстрая адаптация к изменяющимся условиям.

Так как нейронная сеть не требует наличия формальной модели, то с ее помощью можно создать модель для прогнозирования времени ожидания в очереди как нелинейную функцию ряда параметров, которые учитывают не абсолютные (как в выражении 1),   а относительные величины.

 

Решение задачи прогнозирования времени ожидания в очереди.

 

Для того чтобы решить задачу прогнозирования изменения времени ожидания в очереди с помощью нейронных сетей предлагается в процессе обработки статистических данных извлекать следующую информацию:

·       долю длинных сигнальных единиц в потоке;

·        долю интервалов между поступлением сигнальных сообщений, принимающих значения меньше среднего интервала;

·       отношение средней длительности интервала между поступлением к средней длительности обслуживания сигнальных сообщений;

·       интенсивность загрузки звена сигнализации.

Анализ процесса поступления сигнальных единиц на звено сигнализации показал, что длина сигнальных единиц изменяется от 16 до 70 байт.

 

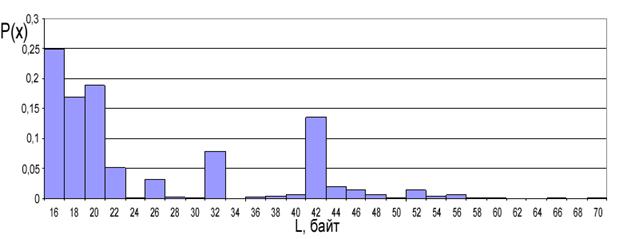
Рис. 1.

Гистограмма длин сигнальных единиц в исходной выборке.

 

Переменную длину имеют сообщения типа IAM (начальное адресное сообщение), остальные типы сигнальных единиц имеют постоянную длину. Был определен набор типов сообщений, встречающихся в выборке, их длина и вероятность появления. В таблице 1 приведены типы сигнальных сообщений, их длина и доля в выборке.

 

Таблица 1.

Характеристика сообщений, встречающихся в выборке.

Тип сообщения	Длина сигнальных сообщений, байт		Доля сообщений в общем потоке, %
	Формируемая ISUP	Полная
IAM	24-63	31-70	22.0
ACM	12	19	15.41
ANM	11	18	8,04
RLC	13	20	21.97
REL	9	16	22,03
остальные	14	21	10,55

 

Из таблицы 1 видно, что доля длинных сообщений составляет четверть общего объема в выборке, в соответствии с процедурой сигнализации при установлении и разъединении соединений. Одно сообщение IAM порождает четыре сигнальные единицы при удачной и две сигнальные единицы при неудачной попытке установления соединения. Кроме того, при предоставлении дополнительных услуг передаются и необязательные сообщения переменной длины. Таким образом, доля длинных сообщений  в разных выборках может изменяться в пределах 20% - 30%  от общего числа сообщений в потоке.

Следующий параметр, влияющий на длину очереди - доля интервалов между поступлением сигнальных сообщений, принимающих значения меньше среднего интервала (). Наибольший интерес представляют малые интервалы между поступлениями сигнальных единиц, так как именно они оказывают существенное влияние на длину очереди. Проведенный анализ показал, что для определения величины  необходимо найти основные статистические характеристики потока и построить гистограмму интервалов между поступлением сигнальных сообщений, причем интервал между поступлением сигнальных единиц необходимо задавать в долях среднего интервала между поступлениями сигнальных единиц.

На рисунке 2 приведен пример гистограммы для выборочной совокупности при с.

 

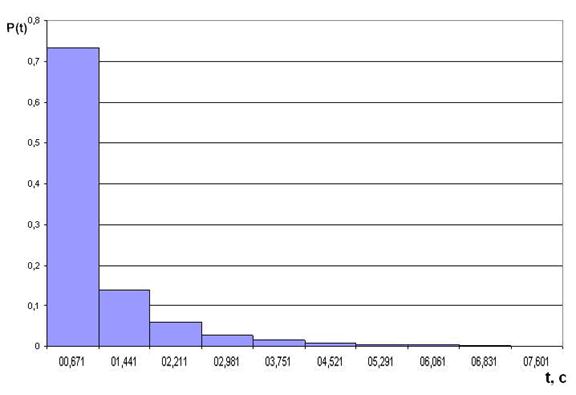
Рис. 2.

Гистограмма  распределения интервалов между поступлением сигнальных сообщений.

 

На рисунке 2 видно, что доля интервалов, меньших, чем средняя  длительность интервалов между поступлениями сообщений,  составляет 73% от общего числа интервалов. Статистический анализ работы звеньев сигнализации показал, что величина  для различных выборок может изменяться от 70% до 80%.

Кроме того, существенное влияние на длину очереди отказывает отношение средней длительности интервала между поступлением () к средней длительности обслуживания сигнальных сообщений (τ).

Четвертый параметр – параметр потока – можно определить как отношение числа поступивших сигнальных сообщений  к длительности интервала мониторинга .

В качестве математической модели для расчета времени ожидания сигнальных сообщений предлагается использовать нелинейную функцию параметров , :

,                                (2)

Эти параметры были использованы при создании обучающего задачника, предназначенного для обучения нейронной сети.

Чтобы решить задачу прогнозирования времени ожидания сигнальных сообщений в очереди, была построена нейронная сеть, обучаемая по алгоритму обратного распространения ошибок. Выбор данного алгоритма обусловлен тем, что он позволяет формальным образом «обучить» нейронную сеть прогнози­рованию изменения требуемой величины на основе ретроспективных данных о самой величине [4]. Алгоритм построения нейронной сети заключается в следующем. На первом шаге были опре­делены базовые статистические ха­рактеристики, используемые при прогнозировании времени ожида­нии в очереди. На втором шаге произво­ди­лось формирование образов, по­да­ваемых непосредственно на входы нейронной сети, то есть  создание обучающих и тестовых множеств. Далее с использованием вы­бранного алгоритма обучения про­изводилось обучение нейронной сети и ее тестирование на тестовом множестве. При удовлетворительной точности работы нейронной сети на тестовом множестве можно счи­тать, что нейронная сеть построена и может использоваться для про­гнозирования.

Задача прогнозирования ре­шалась с помощью многослойной нейронной сети, которая состоит из 4-х нейронов во входном слое (по количеству входных переменных) и 1-го нейрона в выходном слое. Число скрытых слоев и количество ней­ронов в этих слоях определялось экспериментально. Для составле­ния задачника были использованы статистические данные о работе звеньев сигнальной сети, собран­ные в течение двух месяцев.

В силу того, что соответствие между входами и выходами носит явно выраженный нелинейный характер, поэтому использовалась нейронная сеть с нелинейными сигмоидальными функциями активации [8].

Для проведения сравнительного анализа алгоритмов обучения использовались два критерия: средняя абсолютная погрешность обучения и количество эпох обучения [6].

Для определения оптимального числа нейронов в скрытом слое рассматриваемой нейронной сети применялся  пакет Matlab [6].  При изменении  числа нейронов в скрытом слое фиксировалось количество эпох обучения. В ходе проведенных экспериментов для различных алгоритмов обучения были получены кривые зависимости времени обучения нейронной сети от количества нейронов в скрытом слое (рисунок 3).

 

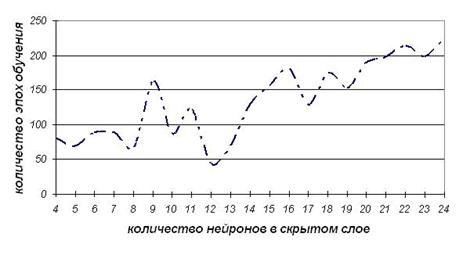
А.

 

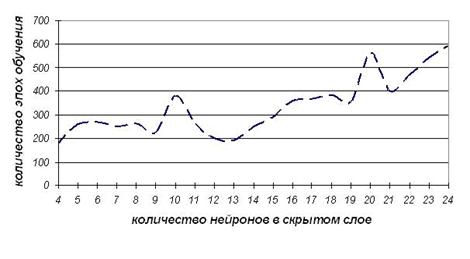
Б.

 

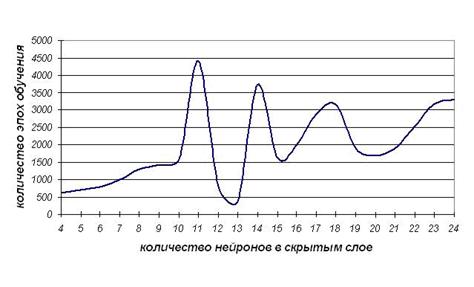
В.

 

Рис. 3.

Зависимость времени обучения нейронной сети от количества нейронов в скрытом слое для трех алгоритмов обучения.

А) алго­ритм оптимизации Левен­берга-Марквардта;

Б) АОР в сочетании с методом Флетчера-Пауэлла;

В) АОР с использованием метода секущих.

 

Проведенный сравнительный анализ алгоритмов обучения нейронных сетей показал, что оптимальное соотношение количества эпох и качества обучения достигается при 12 нейронах в скрытом слое.

В таблице 2 приведен сравнительный анализ модификаций алгоритма обратного распространения (АОР) для структуры 4х12х1.

 

Таблица 2.

Сравнение модификаций алгоритма обратного распространения.

        

Таким образом, наиболее предпочтительными можно считать алгоритмы оптимизации Левенберга-Марквардта,  Флетчера-Пауэлла  и квазиньютонов­ский. Наихудшие показатели имеют алгоритмы градиентного спуска (тре­буемая точность не была достигнута).

Далее на тестовой выборке из потока сигнальных сообщений  вычислялась средняя абсолютная погрешность и дисперсия ошибки с использованием следующих алгоритмов оптимизации: квазиньютоновского, Левенберга-Марквардта, Флетчера-Пауэлла (таблица 3).

 

Таблица 3.

Средняя абсолютная погрешность и дисперсия ошибки.

Функция обучения	Параметр	Величина
Квазиньютоновский АОР	Средняя абсолютная погрешность	0,42
	Дисперсия погрешности	0,31
Алгоритм оптимизации Левенберга-Марквардта	Средняя абсолютная погрешность	0,38
	Дисперсия погрешности	0,18
АОР в сочетании с методом Флетчера-Пауэлла	Средняя абсолютная погрешность	0,81
	Дисперсия погрешности	0,34

 

Анализ таблицы 3 показал, что наименьшую погрешность прогнозирования на тестовой выборке дает алгоритм оптимизации Левенберга-Марквардта

Таким образом, для прогнозирования изменения времени ожидания в очереди была построена нейронная сеть со структурой 4х12х1.

Математическую модель разработанной нейронной сети можно представить в виде:

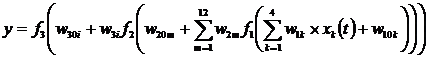,  (3)

где  – число нейронов первого слоя;  - число нейронов второго слоя; – число нейронов третьего слоя; - начальные возбуждения k-го, m-го, i-го нейронов первого, второго и третьего слоев.

В таблице 4 приведен пример расчета и сравнения результатов прогноза времени ожидания в очереди с помощью модели СМО G/G/1 (выражение 1) и с помощью аппарата нейронных сетей (НС) на основании статистических данных звена сигнализации.

 

Таблица 4.

Основные статистические характеристики выборки и расчет времени ожидания в очереди с помощью модели СМО G/G/1 и аппарата нейронных сетей (НС).

Интервал наблюдений	Характеристика выборки				времени ожидания в очереди, мс		Погрешность%
	Средняя  длит. интервалов , мс	Стандартное отклонение ,  мс	Стандартное отклонение , мс	интенсивность поступающей нагрузки р, Эрл	модель G/G/1	НС
1	0.12	0.15	1,31	0,03	7,47	7,49	2,1
2	0.65	0.95	1,31	0,03	2,08	1,99	4,1
3	0.21	0.29	1,31	0,03	4,42	4,46	3,8
4	0.24	0.31	1,31	0,03	3,89	3,94	4,7
5	0.08	0.09	1,31	0,03	11,11	11,07	4,4
6	0.11	0.13	1,31	0,03	8,12	8,09	2,9
7	0.09	0.11	1,31	0,03	9,90	9,93	2,9
8	0.13	0.15	1,31	0,03	6,89	6,93	3,7
9	0.16	0.22	1,31	0,03	5,68	5,65	3,6

 

По результатам сравнения полученных результатов с результатами расчета (таблица 4) был сделан вывод, что отклонения прогнозируемых значений от рассчитанных аналитически не превышает 4.7%.

Таким образом, разработанная методика прогнозирования на основе аппарата нейронных сетей позволила администратору сигнальной сети решить задачу оперативного прогнозирования времени ожидания в очереди, опираясь  не на абсолютные,  а относительные величины.

 

Литература.

 

1. ITU-T. SWITCHING AND SIGNALLING. Specifications of Signalling System No. 7 – Signalling System No. 7 Management. Recommendation  Q.752 (06/97).

2. Гольдштейн Б.С. Перегрузки и мониторинг сети сигнализации ОКС-7. // Сети и системы. – 2003 - №3.

3. Гольдштейн Б.С. Сетевой мониторинг: проблемы и решения. // Вестник связи. – 2002 - №2.

4. Каллан Р. Основные концепции нейронных сетей.: Пер. с англ. – М.: Издательский дом «Вильямс», 2001. – 287 с.

5. Крылов В.В., Самохвалова С.С. Теория телетрафика и ее приложения. - СПб.: БХВ-Петербург, 2005. – 288 с.

6. Медведев В.С., Потемкин В.Г. Нейронные сети. MATLAB 6 / Под общ. ред. к. т. н. В.Г. Потемкина – М.: ДИАЛОГ-МИФИ, 2002. – 496 с.

7. МККТТ. Синяя книга. Подсистема пользователя цифровой сети с интеграцией служб Q.761-Q.767– Женева, 1993.

8. Осовский С. Нейронные сети для обработки информации /Пер. с польского И.Д. Рудинского. – М.: Финансы и статистика, 2002. – 344 с.

9. Росляков А.В. Общеканальная система сигнализации №7. – М.: Эко-Трендз, 1999, 176 с.

 

Поступила в редакцию 13.03.2008 г.