Исследования закономерностей спектрообразования сложных сигналов, реализуемых методами
широтно-импульсной модуляции
Мирманов Арман Барлыкович,
аспирант кафедры радиопередающих
устройств и электропитания Сибирского государственного университета телекоммуникаций
и информатики.
В статье исследуются спектральные
характеристики напряжений источников переменного тока синтезируемых импульсными
методами, реализуемых методами широтно-импульсной модуляции и представляемых
набором элементарных. Получены расчетные
выражения для вычисления гармонических составляющих двух типов сигналов и определены
пути для улучшения их качества.
В условиях участившихся природных
катаклизмов, физического износа электрических сетей общего пользования и т.н.
человеческого фактора, сбои в системах энергообеспечения «критических» потребителей вызывают многомиллионные ущербы. Один из
принципов обеспечения энергетической безопасности информационных и телекоммуникационных
систем и, в частности, их независимости от качества электрических сетей общего
пользования, базируется на кондиционировании сетей с помощью двухкаскадных
(зеркальных) преобразователей типа – AC/DC - DC/AC с использованием в промежуточной
точке каскада резервного источника энергии постоянного тока. Выходное
напряжение в таких системах формируется каскадом DC/AC, называемого инвертором
напряжения (ИН). Таким образом, для критического потребителя (потребителя особой
группы первой категории [1]) ИН является непосредственным источником энергии, и
поэтому должен удовлетворять жёстким нормативным показателям качества генерируемой
энергии переменного тока [2].
Термины «генерирование» и «инвертирование»,
используемые в разных технических дисциплинах, в данном контексте является
аналогами, т. к. отражают факт преобразования в автономном звене электрической
энергии постоянного тока в энергию переменного тока. Заметим, что современные
технологии преобразования энергии ориентируются на импульсные методы, при этом
«первичный» продукт преобразования
напряжения на выходе импульсного звена (рисунок 1) представляет
периодический ансамбль импульсов с определенной спектральной структурой. С
помощью последующего линейного звена (фильтра) структура сигнала и его спектра
преобразуются, при этом параметры фильтра, а вместе с ними и динамические и технико-экономические
характеристики ИН во многом определяются спектром сигнала U1, а следовательно, «архитектурой» ансамбля импульсов,
образующих его волну напряжения.
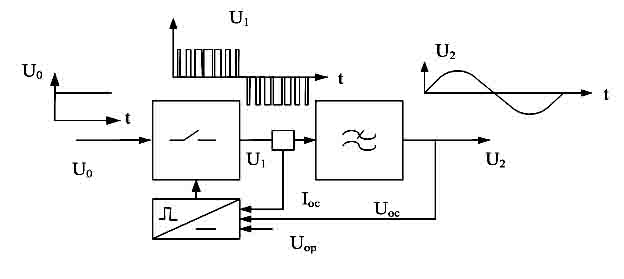
Рис. 1. Функциональная схема
формирования напряжения.
Сложившиеся подходы описания подобных
сигналов, ориентированные на элементы классической теории широтно-импульсной
модуляции (ШИМ) [3, 4], дают общие представления о закономерностях спектрообразования сигналов; вместе с тем, ряд аспектов,
важных для инженерной практики не могут быть учтены сложившимися подходами. В
качестве примера назовем не реализуемость в мощных «энергетических» приложениях импульсов «малой» длительности (менее 0,2…0,5
мкс), требуемых по условию получения допустимых искажений формируемого
напряжения; неопределенность условий отсутствия низкочастотных «шумов»
квантования в спектре сигнала; неопределенность картины распределения энергии в
спектральных группах сигналов и ряд других. Предлагаемый в настоящей работе
подход, названный «синтезом напряжения» ориентирован на возможность
представления сложного ансамбля линейной комбинацией элементарных сигналов с
известными временными, спектральными характеристиками и взаимными фазовыми соотношениями.
Задача анализа упрощается при представлении ансамбля четной функцией времени.
Необходимым условием этого является целочисленность и
четность значения кратности тактовой частоты ШИМ (М) по отношению к частоте
синтезируемого сигнала для однополярного ансамбля импульсов в полуволне (ОШИМ),
и нечетность значения М для двухполярного ансамбля
импульсов (ДШИМ) [4]. Примеры названных типов сигналов, реализуемых в однофазных ИН при постоянной тактовой частоте ШИМ, показаны
на рисунке 2.
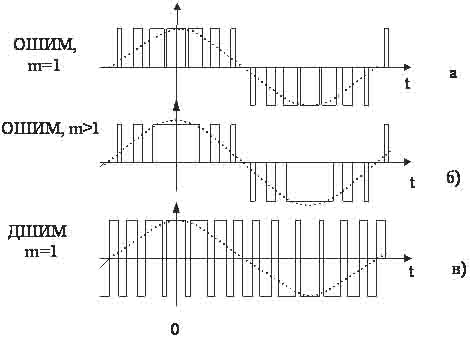
Рис. 2. Примеры ШИМ сигналов на выходе
импульсного звена ИН.
Пунктиром обозначена основная гармоника сигнала
при коэффициенте регулирования (модуляции) m=1 и m>1.0.
Штриховкой обозначены элементарные импульсные сигналы ансамбля, двухполярные
для ОШИМ и однополярные для ДШИМ. При
таком представлении сигналов они могут быть суммой конечного числа элементарных
сигналов s(n).
А. Сигнал ОШИМ:
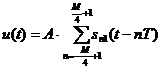(1)
Б. Сигнал ДШИМ:
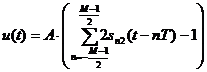, (2)
где А -
высота импульсов в ансамбле, n - порядковый номер
элементарной функции, sn1, sn2
- двухполярная и однополярная стробирующие
функции, с относительными
длительностями импульсов Dn1, Dn2,
соответственно, определяемыми значениями функции выборки эталонного сигнала
задания («образа» основной составляющей синтезируемого сигнала) (
,
).
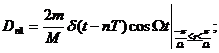
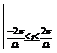. (3)
Заметим, что набор значений Dn1, Dn2 образуют
решетчатые функции с периодом тактовой (несущей) частоты Т, модулированные по амплитуде опорным гармоническим сигналом
(рисунок 3а,б). Их спектры амплитуд (Сk=f(k), k-порядковый номер гармоники),
полученные методом ДПФ [5], показаны на рисунке 3в,г.
А). ОШИМ:
,
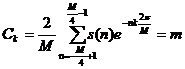для k=1,
nM-1, nM+1,
(4)
для всех остальных значений k.
Б) ДШИМ:
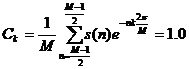
для k=nM,
Ck=m (5)
для k=nM-2,
k=nM+2.
Спектральные диаграммы наглядно иллюстрируют
особенности формирования побочных
гармоник, сгруппированных в окрестности частот с кратностью М, 2М…nM. В
последующем это позволит ввести понятие «эквивалентного» напряжения групповой помехи,
приведенной к частоте 
. Диаграмма рисунок 3в иллюстрирует присутствие в спектре
дискретной последовательности Dn2
постоянной составляющей. Её подавление в спектре реального сигнала ДШИМ
обеспечивается слагаемым «-1» в выражении (2). Отметим также факт различия
спектральных групп сигналов, связанный с подавлением помехи с таковой частотой в
сигнале ОШИМ.
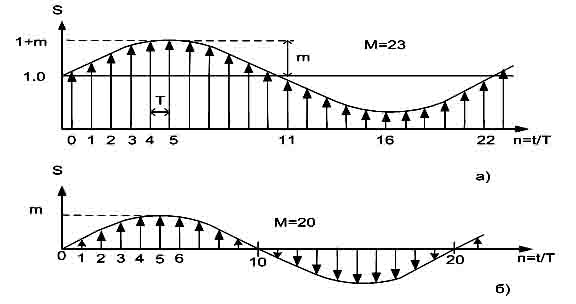
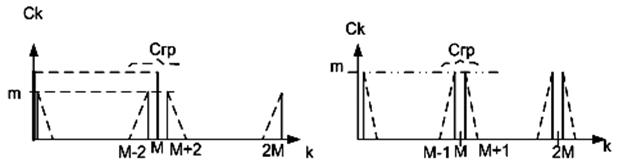
в) г)
Рис. 3. Дискретные сигналы ОШИМ и ДШИМ и
их спектры.
Из диаграмм следует частный вывод о некоторых
причинах
возможного отклонения спектров реальных сигналов от
рассмотренных дискретных:
-
модулирующий
сигнал отличается от гармонического и в его спектре присутствуют
составляющие низких порядков кратности;
-
при
реализации ансамбля сигналов нарушено условие передачи всех М дискретных его компонент;
-
спектральные
плотности элементарных сигналов отличаются от
спектральной плотности функции отсчетов;
-
квантование
образцового сигнала по уровню при относительно малом разрешении АЦП.
В итоге спектральная диаграмма реального
сигнала может отличаться от рассмотренного идеализированного
«размыванием» спектральных групп (на рис. 3 обозначено пунктирными линиями).
Переходя от функции отсчетов к стробирующим функциям, обозначенными как «элементарные» составляющие (sn1 или sn2) синтезируемой волны напряжения, запишем решения для
амплитуд гармоник при представлении s(n)
четной функцией времени с высотой импульса Аn
и относительной длительностью импульса Dn:
А. ОШИМ:
, (6)
где 
,
k=1,3.5…
Б. ДШИМ:
, (7)
где 
,
k=0,1,2,3.…
Зависимость амплитуд гармонических
составляющих от их номера (k) определяется сомножителем s(x) = sin(x)/x. Это означает,
что в области значений k=1…k0, в которой s(x)»1,0, гармоники равны величине 2AnDn/M. Следовательно,
по аналогии с решетчатыми функциями, для которых uk=const=Dn, в спектре ансамблей функций, описываемых выражениями
(1), (2) первые гармоники (k=1)
элементарных составляющих суммируются, остальные гармоники взаимно
компенсируются. С ростом кратности тактовой частоты (М) значение k0
возрастает. Анализ показывает, что для s(x)»1,0 при М=200,
400, 800 (что соответствует тактовой частоте ШИМ f = 10, 20 и 40 кГц, соответственно) k0 близки к значениям 50, 125, 200. Важно отметить
также, что при условии s(x)»1,0, амплитуды гармоник пропорциональны площади
элементарных сигналов. Это означает, что фрагменты сигналов, сформированные из
импульсов малой длительности, нереализуемой в сильноточных приложениях из-за
ограниченного быстродействия ключей, без потери качества могут быть организованы
из импульсов с относительно большой длительностью, но с пропорционально
уменьшенной амплитудой. Другими словами, одноуровневая
огибающая импульсной последовательности сигнала может быть заменена ступенчатой,
со снижением уровня «по краям полуволны» синтезируемого образцового сигнала.
Используя принцип линейной комбинации, запишем
решения для гармонических составляющих ОШИМ и ДШИМ сигналов. С учетом (3), (5)
и (7) находим:
А. Одноуровневый ОШИМ:
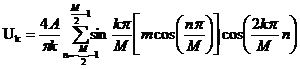, (8)
Б. Двухуровневый ОШИМ:
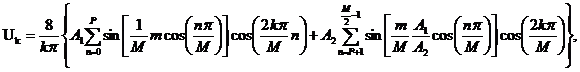(9)
где р - число стробирующих функций в ансамбле с уровнем А1.
В. Сигнал ДШИМ:
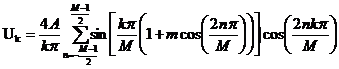. (10)
Спектральные диаграммы, полученные по
формулам (8), (10) для частного случая m=1,0,
A=1,0 показаны на рисунке 4. Структуры
диаграмм совпадают с полученными ранее для решетчатых
функций. Основное различие заключается в образовании в окрестности частот с
кратностью M по отношению к частоте
синтезируемого сигнала гармоник, образующих «групповую узкополосую» помеху с
эквивалентной амплитудой
Uгр(n)=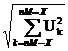
.
Индексы «n» в приведенном выражении определяют
номер группы, Х - число значимых
составляющих спектра помехи. Для практических приложений весьма важное значение имеет группа первого порядка (n=1), определяющая требования к
фильтровым устройствам ИН. В таблице 1 приведен ряд значений гармоник первой
группы сигналов ОШИМ и ДШИМ и эквивалентные значения помехи их первой группы.
Таблица наглядно иллюстрирует
«преимущество» сигнала ОШИМ, связанное с отсутствием в его спектре
гармоники с несущей частотой (k=M).
Соответственно, эквивалентное значение помехи первой группы у сигнала ОШИМ
ниже, чем у сигнала ДШИМ.
Таблица 1.
Значения
компонент сигналов ОШИМ и ДШИМ и их показателей качества.
|
Сигнал |
ОШИМ |
ДШИМ |
||||
|
m= U1m |
1,0 |
0,8 |
0,5 |
1,0 |
0,8 |
0,5 |
|
Д |
1,128 |
1,006 |
0,7955 |
1.41 |
||
|
Uгр1 |
0,1966 |
0,229 |
0,268 |
0,746 |
0,873 |
1,09 |
|
cos(c1) |
0,888 |
0,795 |
0,627 |
0,801 |
0,675 |
0,417 |
|
tg(c1) |
0,395 |
0,607 |
0,975 |
0,952 |
0,956 |
2,18 |
Литература.
1.
ГОСТ Р 50571. 1-93 (МЭК 446-89) Электроустановки зданий. Общие
положения.
2.
ГОСТ
13109-97 Нормы качества электрической энергии в системах электроснабжения
общего применения.
3.
Дмитриков В.Ф., Петяшин Н.Б., Сиверс М.А.
Высокоэффективные формирователи гармонических колебаний. – М.: Радио и связь,
1988.
4.
Kjeld Thorborg. Power electronics.-NY.: Prentis Hall. 1988.
5.
А.Б.
Сергиенко. Цифровая обработка сигналов. – СПб.: Питер.
1999.
Поступила в редакцию 13.10.2008
г.