Математическое описание систем управления в нормальной форме пространства состояний

Прошин Иван Александрович,

доктор технических наук, профессор,

Прошин Дмитрий Иванович,

кандидат технических наук, доцент,

Прошина Раиса Дмитриевна,

соискатель,

Пензенская государственная технологическая академия.

Пусть линейная стационарная одномерная система управления с входным воздействием  и выходной координатой  описывается моделью в виде дифференциального уравнения n-го порядка с постоянными коэффициентами  и  в форме «Вход – выход»

Озонатор промышленный

озонаторы от производителя. Гарантия качества

tk-pozitron.ru

или

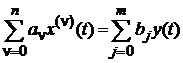                                                                                    (1)

Традиционно математическую модель (1) в нормальной форме пространства состояний для систем с  записывают так [1, 2]:

;

.                                                                       (2)

В качестве переменных состояния  при представлении математических моделей (1) систем управления в нормальной форме пространства состояний выбираются выходная величина  и  ее производные.

Коэффициенты  при этом вычисляют по формулам

; .

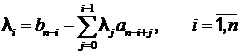Если степень числителя передаточной функции, соответствующей исходному дифференциальному уравнению, меньше степени знаменателя , коэффициенты  полагают равными нулю.

Анализ модели (2) показывает, что входное воздействие в системе при  подаётся на вход последнего блока, а выходная координата формируется по первой переменной состояния. Так как каждая переменная состояния вычисляется на основе значений последующей переменной, то при численном интегрировании системы уравнений (2) на первом шаге при  в функции входной переменной вычисляется только переменная состояния, на втором шаге переменная и т.д., то есть передача сигнала в системе происходит последовательно от последнего блока к первому, что противоречит естественному прямому порядку вычислений и принципу причинности.

С целью получения математической модели системы в форме пространства состояний с прямой причинно-следственной связью предлагается переменные  в (1) вводить, начиная с n-й компоненты вектора состояния [3, 4]. Зададим для системы с  переменные состояния v₁, v₂, ..., v_n, связанные с выходной величиной x(t) и ее производными, соотношениями:

                                                                             (3)

Отличие введённых координат состояния (3) состоит в том, что в качестве й компоненты вектора состояния принята выходная переменная системы, а первой компоненте вектора состояния соответствует производная выходной переменной. С учётом предложенного подхода в матричной форме пространства состояний система уравнений запишется так [5]:

;

.                                                                     (4)

В модели системы управления в пространстве состояний нормальной формы (4), полученной на основании предложенного подхода, первая компонента  непосредственно зависит от входного воздействия, а каждый последующий элемент вектора состояния вычисляется с использованием предыдущей переменной (вторая фазовая координата зависит от первой и т.д.). Выход системы формируется по й компоненте вектора состояния, являющейся в свою очередь функцией й компоненты фазовых координат, а следовательно и всех других координат состояния.

С целью исключения производных от входной величины в дифференциальных уравнениях для систем управления с моделями, содержащими  полюсов и  нулей, введем новые переменные состояния: , :

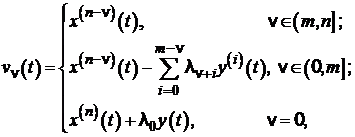                                        (5)

Коэффициенты при производных в правых частях дифференциальных уравнений (5) равны нулю при условиях

Откуда следует рекуррентная формула для вычисления численных значений коэффициентов

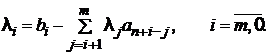                                                               (6)

В общем случае для системы управления, передаточные функции которых содержат  полюсов и  нулей, математическая модель в нормальной форме пространства состояний в соответствии с предложенным подходом и (6) может быть представлена в виде

;

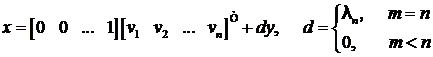.                    (7)

Таким образом, предложенный подход к построению математических моделей в пространстве состояний нормальной формы позволяет записать модель системы управления с учётом прямой причинно-следственной связи (7) и избежать погрешностей при моделировании систем на компьютерах. Разработанная математическая модель обеспечивает единство методологических принципов при исследовании, анализе и синтезе систем управления по моделям «Вход – выход» и «Вход – состояние – выход».

Литература

1.                  Алексеев А.А., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория управления. – СПб.: Изд-во СПбГЭТУ “ЛЭТИ”, 1999. – 435 с.

2.                  Методы классической и современной теории автоматического управления: Учебник в 3-х т. Т1: Анализ и статистическая динамика систем автоматического управления / Под ред. Н.Д. Егупова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 748 с.

3.                  Прошин И. А. Принцип причинности в математическом описании систем управления в пространстве состояний// Проблемы технического управления в региональной энергетике: Сборник статей по материалам научно-технической конференции. – Пенза, 2001. С. 17 – 23.

4.                  Прошин И. А. Выбор фазовых координат модели системы управления в нормальной форме пространства состояний// Проблемы технического управления в региональной энергетике: Сборник статей по материалам научно-технической конференции. – Пенза, 2001. С. 23 – 27.

5.                  Прошин И. А. Математическое описание систем управления в нормальной форме пространства состояний. // Проблемы технического управления в региональной энергетике: Сборник статей по материалам научно-технической конференции. – Пенза, 2001. С. 27 – 34.

Поступила в редакцию 20.04.2009 г.