Поиск на неточное соответствие: коды Хемминга

 

Харитоненков Андрей Валерьевич,

аспирант Санкт-Петербургского государственного университета культуры и искусств,

менеджер проектов Квестор Ай Ти.

Научный руководитель - доктор технических наук, профессор

Вершинина Лилия Павловна.

 

В связи с бурным развитием информационных технологий и непрерывным увеличением объемов информации, доступной в глобальной сети Интернет, всё большую актуальность приобретают вопросы эффективного поиска и доступа к данным.

Зачастую стандартный поиск с использованием ключевых слов не даёт желаемого результата, в связи с тем, что такой подход не учитывает языковые и смысловые взаимосвязи между словами запроса.

Большинство пользователей ищут информацию, просто, вводя в поисковую форму одно или несколько ключевых слов для поиска и не применяют сложных функций булевой логики, поэтому поисковый механизм сам должен быть достаточно интеллектуальным.

Как показывает практика, довольно сложно найти нужную информацию используя только поиск на точное совпадение ключевых слов. Слова могут встречаться в документах абсолютно в различных формах, отличающихся от исходных форм, указанных в поисковом запросе. Поэтому практически все современные поисковые системы используют при поиске грамматическую нормализацию слов, т.е. ищут документы, не только по точному совпадению ключевых слов запроса, но и по различным грамматическим формам одного и того же слова. Однако даже грамматической нормализации оказывается порой недостаточно.

На практике, довольно часто, приходится искать что-либо, обладая ограниченным количеством информации и даже порой, не зная точного написания поисковой фразы. Допустим, мы ищем какую-то цитату или высказывание из книги, но не помним его дословно или лекарство, название которого так же плохо запомнили и допустили ошибку в написании.

При вводе информации, например при сканировании, с бумажных носителей в БД неизбежно искажение информации, ошибки и опечатки разной степени тяжести, что затрудняет последующий поиск и делает практически невозможным.

Кроме стандартного поиска по ключевым словам, основам и нормальным грамматическим формам возникает необходимость в поиске похожих слов, получающихся из слов исходного поискового запроса в результате ошибок, опечаток и искажений, связанных с различным написанием одинаково звучащих слов. Таким образом, остро встает проблема поиска документов неточно соответствующих поисковому шаблону.

Поисковая система должна дополнять вводимый пользователем запрос ассоциативно связанными и близкими по значению словами.

 Один из способов повышения точности результатов поиска - нечеткий поиск по сходству с дополнением запроса синонимами ключевых слов.

Обычные алгоритмы поиска выполняют проверку на точное совпадение строк. Как пример, хорошо известный оператор LIKE в языке SQL. Этот оператор часто используется для организации поиска по строковым полям в таблицах баз данных. Он допускает использовать при поиске шаблоны, в которых символами «%» можно обозначить не имеющие значения части строки.

Традиционные алгоритмы сравнения строк дают только два ответа - равны данные строки или нет. Алгоритмы нечеткого поиска дают более расширенный ответ - насколько отличаются строки друг от друга. Для этого в этих алгоритмах используется понятие «расстояние редактирования». Данное понятие показывает, сколько операций нужно применить к первой строке, чтобы получить вторую строку.

Чтобы из строки «карова» получить строку «корова» достаточно поменять вторую букву «а» на «о». Это одна операция и расстояние редактирования между этими строками будет равно единице. Как и для строк «крова» и «корова», в которых достаточно добавить букву «о» во вторую позицию.

В алгоритм вычисления расстояния редактирования можно внести различные веса для различных операций. И даже для различных символов. Это будет полезно для определения опечаток при контроле ввода пользователя, или же при обработке результатов распознавания текста.

Технология нечеткого поиска позволяет расширять запрос близкими по написанию словами, содержащимися в коллекции документов, по которым ведется поиск. Алгоритм нечеткого поиска способен найти все лексикографически близкие слова, отличающиеся заменами, пропусками и вставками символов.

Нечеткий поиск целесообразно применять при поиске слов с опечатками, а также в тех случаях, когда возникают сомнения в правильном написании - фамилии, названия организации и т.п. [5]. Например, запрос «инкомбанк» может быть расширен словами: «инкомбан», «инкобанки», «винкомбанке».

Поиск по сходству, с расширением ключевых слов активно применяется в системах проверки орфографии, например в широко известный программный комплекс Microsoft Office встроен модуль проверки правописания, который использует в своей работе алгоритмы поиска и замены ошибочного слова ассоциативно близкими по значению словами.

Модули проверки орфографии, или как их называют «спеллчекеры» используются и в поисковых системах, для проверки правильности написания слов запроса.

Однако, алгоритмы нечеткого поиска по сходству пока, что практически не реализованы в современных поисковых системах.

Нечеткий поиск по сходству может быть реализован на базе различных алгоритмов и функций поиска.

В настоящее время для реализации поиска на неточное соответствие используются следующие методы:

1)                  перебор или сканирование словаря;

2)                  расширение выборки или метод спел-чекера;

3)                  методы n-грамм;

4)                  хеширование;

5)                  триангуляционные деревья;

6)                  trie-деревья (лучи).

Для лучшего понимания технологий поиска по сходству дадим краткий обзор данных алгоритмов.

Метод сканирования словаря заключается в последовательном считывании данных с диска и сравнение с термином запроса. Основным достоинством этого метода является простота реализации и, как это ни странно, довольно высокая скорость работы. Дело в том, что при последовательном считывании больших файлов (при условии невысокой фрагментации на диске) достигается пиковая скорость чтения. Кроме того, этот метод позволяет реализовать многофункциональный поиск, например, по подстроке или регулярным выражениям, без каких-либо существенных ограничений.

Метод расширения выборки широко используется программами проверки орфографии. Данный метод подразумевает построение наиболее вероятных «неправильных» вариантов поискового шаблона.

Т.е. строится множество всевозможных «ошибочных» слов, например, получающихся из исходного в результате одной операции редактирования, после чего построенные термины ищутся в словаре на точное соответствие.

Поисковый шаблон, как правило, содержит слова, для которых расстояние редактирования до исходного шаблона не больше 1. Таким образом, задача поиска на неточное равенство сводится к задаче поиска на точное равенство. Кроме обычных ошибок программа проверки орфографии так же может сделать предположение об изменении формы слова.

Метод n-грамм. Суть метода заключается в следующем: если строка  «похожа» на строку u, то у них должны быть какие-либо общие подстроки. Поэтому бывает целесообразно строить инвертированный файл, в котором роль документов играют сами термины, а роль терминов — подстроки длины n, называемые также n-грамами. Данный метод основан на предположении, что при малых искажениях слова должны обладать достаточным количеством общих n-грамм. Основной недостаток метода n-грам — большой размер файла.

Метод хеширования заключается в разработке хеш-функции слова, которая бы определяла его основные характеристики и была устойчива к искажениям слова. Хеш-функция разбивает слова на группы и производит последовательный поиск внутри группы, вычисляемой по поисковому шаблону [1].

В качестве примера хеш-функции можно привести функцию soindex, встроенную в такие СУБД как MS SQL Server и Oracle. Однако метод soindex обеспечивает лишь «частичный» поиск, потому что хеш-функция устойчива только на узком классе искажений и довольно сложно предсказать как они измениться после вставки произвольного символа.

Например, для разбиения на группы иногда используется хеширование по первым двум буквам слова. В качестве примера хеш-функции можно привести функцию soindex, встроенную в такие СУБД, как Subase, MS SQL Server и Oracle.

Trie-деревья. В trie-дереве все строки, имеющие общее начало, располагаются в одном поддереве. Каждое ребро помечено некоторой строкой. Терминальным вершинам («листьям») соответствуют слова списка.

Пусть список строк содержит термины: дерево, деревья, пол, половик; тогда соответствующее ему trie-дерево изображено на рис. 1:

 

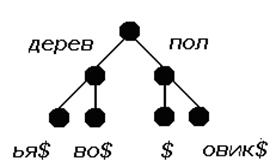
Рис 1.

 

Чтобы ни одно из слов не было префиксом другого слова (как в случае слов пол и половик), в конец каждого слова добавляется специальный символ $, отсутствующий в алфавите.

Обычно trie-деревья используются для поиска по подстроке, но их можно использовать, и весьма эффективно, для поиска по сходству. Чтобы обеспечить поиск по подстроке, необходимо хранить в trie-дереве все суффиксы (или префиксы терминов). При этом, как и в случае метода n-грам размер индекса в 2-10 раз превышает размер словаря.

Триангуляционные деревья. Триангуляционные деревья позволяют индексировать множества произвольной структуры, при условии, что на них задана метрика. Существует довольно много различных модификаций этого метода, но все они не слишком эффективны в случае текстового поиска и чаще используются для организации поиска в базе данных изображений или других сложных объектов [6].

Рассмотрев вкратце основные методы поиска, допускающие неточное задание терминов запроса, перейдем к описанию одной из наиболее перспективных технологий, на базе которых возможна реализация эффективных моделей нечеткого поиска по сходству.

 

Сети Хемминга

Для нечеткого поиска могут быть использованы широко известные алгоритмы и коды Хемминга. Коды Хемминга давно и успешно применяются при кодировании и декодировании информации, позволяя успешно восстановить утерянную пре передачи информацию.

Сети Хемминга так же активно используются для оптического распознавания символов (OСR).

Однако алгоритмы Хемминга могут быть применены не только в теории кодирования информации, но и в вопросах информационного поиска. Особенно эффективно коды Хемминга работают вместе с аппаратом нечеткой логики.

Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку [2].

Сети Хэмминга представляют собой одну из разновидностей нейронных сетей. Принцип работы сетей Хэмминга основан на определении расстояния Хэмминга между объектами и нахождении наиболее близкого.

Алгоритмы Хемминга в своей работе используют линейный код, который по сравнению с другими кодами, позволяют реализовывать более эффективные алгоритмы кодирования и декодирования информации.

В процессе поиска и выдачи информации неизбежно возникают ошибки, поэтому контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией.

Актуальной представляется задача разработки системы нечеткого поиска, которая может находить слово в списке, даже если оно искажено или содержит опечатки и пропущенные символы.

Для обнаружения ошибок в сетях Хемминга используют коды обнаружения ошибок, для исправления — корректирующие коды.

Для этого при записи и передачи информации в полезные данные добавляют специальным образом структурированную избыточную информацию, а при чтении (приеме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.

Таким образом, алгоритмы Хэмминга могут быть использованы для поиска слов, которые в исходном запросе набраны с ошибками.

Предположим у нас на входе есть словарь и необходимо найти искомое слово в этом словаре, даже если оно было набрано с ошибкой. Для этого нужно сначала продумать и разработать систему кодирования символьной информации в вектора. Зададим для каждого символа его битовую маску:

А– 00001

Б – 10001

В – 10010

При кодировании символьной информации необходимо учитывать источник для получения данной информации. Если, допустим, мы вводим символы использую клавиатуру, то целесообразно будет задавать коды символов таким образом, что бы у символов, расположенных рядом на клавиатуре, были бы и близкие по Хеммингу коды. Если же источником является программа распознавания образов (OCR), то близкие коды должны быть у схожих по написанию символов. После кодирования, таким образом, подаем полученные вектора на вход нейронной сети.

Однако необходимо учитывать одну особенность сетей Хемминга. Если при написании была опечатка или даже две, то алгоритм работает хорошо, но если был пропущен символ или добавлен лишний, то Хемингово расстояние может оказаться слишком большим. Для того, чтобы устранить этот недостаток, мы будем подавать на вход, как само искомое слово, так и это же слово, исключая по очереди по одному символу в каждой позиции и добавляя по одной букве в каждую позицию. Такой подход позволит найти практически все случаи ошибок – опечатка, пропуск символа, лишний символ.

Следует отметить, что, не смотря на большую эффективность кодов Хемминга, они не лишены определенных недостатков. Линейные коды, как правило, хорошо справляются с редкими и большими ошибками и опечатками [4]. Однако их эффективность при сравнительно частотных, но небольших ошибках менее высока.

Благодаря линейности для запоминания или перечисления всех кодовых слов достаточно хранить в памяти кодера или декодера существенно меньшую их часть, а именно только те слова, которые образуют базис соответствующего линейного пространства. Это существенно упрощает реализацию устройств кодирования и декодирования и делает линейные коды весьма привлекательными с точки зрения практических задач информационного поиска.

 

Литература

 

1. Бойцов Л.М. Использование хеширования по сигнатуре для поиска по сходству. Прикладная математика и информатика. М. Изд-во факультета ВМиК, МГУ 2000, № 7.

2. Блейхут Р. Теория и практика кодов, контролирующих ошибки/ Р. Блейхут - М.: Мир, 1986.

3. Головко В.А. Нейронные сети: обучение, организация и применение/ В.А. Головко, под ред.проф.А.И.Галушкина - Москва : ИПРЖР, 2001.

4. Стефан А. Анализ строк, перевод М.С.Галкиной под ред. П.Н.Дубнера оригинал: Graham A. Stephen, String Search, Technical Report TR-92-gas-01 School of Electronic Engineering Science , October 1992.

5. Landau G.M., Vishkin U., Fast string matching with k differences, Journal of Computer and System Sciences, Vol. 37, No. 1, p. 63-78. 1988.

6. Информационный поиск и поиск по сходству [электронный ресурс]. − Режим доступа: http://www.itman.narod.ru/, свободный.

 

Поступила в редакцию 21.09.2009 г.