Cтратификация математико-методологической компоненты вектора знаний по степени детализации и уровню овладения знаниями

Прошин Иван Александрович,

доктор технических наук, профессор,

Прошин Дмитрий Иванович,

кандидат технических наук, доцент,

Прошина Раиса Дмитриевна,

соискатель.

Пензенская государственная технологическая академия.

За исходные положения математико-методологической компоненты вектора знаний [1] примем методологические подходы: системный, энергетический, информационно-алгоритмический причинно-следственный, а также требования к профессиональной подготовке по соответствующему направлению. Как уже отмечалось основное требование, определяющее методологию специальностей по направлению «Автоматизация и управление», состоит в обеспечении проектирования автоматизированных систем управления, ключевым для которого является последовательность процедур «Модель – анализ – синтез» (рис. 1).

За основу математических моделей (ММ) для рассматриваемого направления примем структурирование моделей по классам. В качестве узловых, как при обучении на всех ступенях профессиональной подготовки по вектору знаний, так и при проведении исследований, введём математические модели «Вход – выход» и «Вход – состояние – выход», систематизированные на базе принятых в теории управления принципов.

Методологическая основа рассматриваемых специальностей – фундаментальные принципы управления, алгоритмы функционирования, законы управления. Ядро технологических процессов большинства специальностей – основные физические законы механики, гидростатики, гидродинамики, теплотехники, электромагнетизма и др. Центральным элементом любой автоматизированной системы управления является объект управления – устройство (агрегат, механизм, установка), в котором протекает процесс, подлежащий управлению. Поэтому основополагающим для анализа и синтеза систем автоматического управления (САУ) как элементов единой системы проектирования автоматизированных систем управления является единая методология построения математических моделей технологических объектов управления [2, 3] и других элементов систем управления, изучаемых во всех дисциплинах специальности на базе трёх принятых подходов.

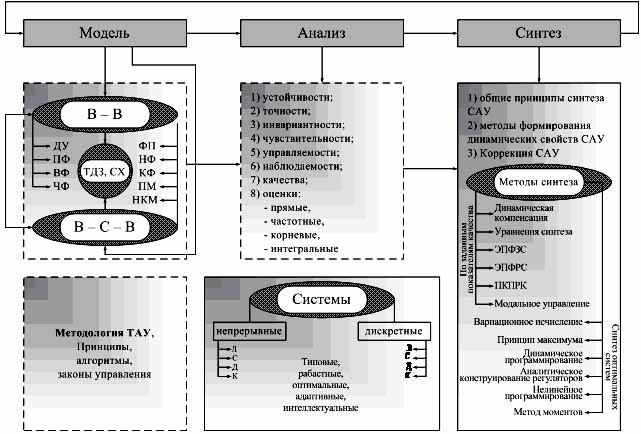
Рис. 1. Тематическая структура математико-методологической компоненты вектора знаний.

Методология анализа систем управления основывается на анализе устойчивости, управляемости, наблюдаемости, чувствительности, инвариантности, точности в установившихся режимах, качества, включая прямые, частотные, корневые и интегральные оценки качества. Изучение основ синтеза систем управления, прежде всего, включает в себя освоение всех этапов проектирования САУ, включая общие принципы топологического, структурного и параметрического синтеза, методы формирования динамических свойств САУ, коррекцию САУ введением местных обратных связей, и обратных связей по производным. Базовыми являются две группы методов. Методы синтеза по заданным показателям качества и методы оптимального синтеза систем с использованием оптимизационных процедур.

Важным является не только изучение основ математико-методологической компоненты в соответствующих дисциплинах, но и непрерывное использование этих знаний на всех этапах профессиональной подготовки при освоении всех других компонент вектора знаний как целостной системы знаний, неизменное расширение и совершенствование багажа знаний математико-методологических основ специальности.

Математико-методологическая компонента по специальности «Автоматизация технологических процессов и производств» объединяет весь комплекс дисциплин (рис. 2) на всех этапах профессиональной подготовки и проектирования систем управления в целостную систему на базе единых принципов систематизации математических моделей «Вход – выход» и «Вход – состояние – выход».

Определяющими для формирования знаний по математико-методологической компоненте на первом курсе примем дисциплины: «Введение в специальность», «Основы инженерного творчества», «Теория решения изобретательских задач», «Математика».

Дисциплина «Введение в специальность» объединяет на первом курсе все компоненты вектора знаний специальности и является методологической основой на первом уровне профессиональной подготовки. Эта дисциплина выполняет задачу обобщения и формирования целостного представления специальности. Определяет как основу автоматизации объекты управления и автоматизации. Даёт представление об использовании при организации технологических процессов основных законов физики, знакомит обучающихся с их математическим описанием.

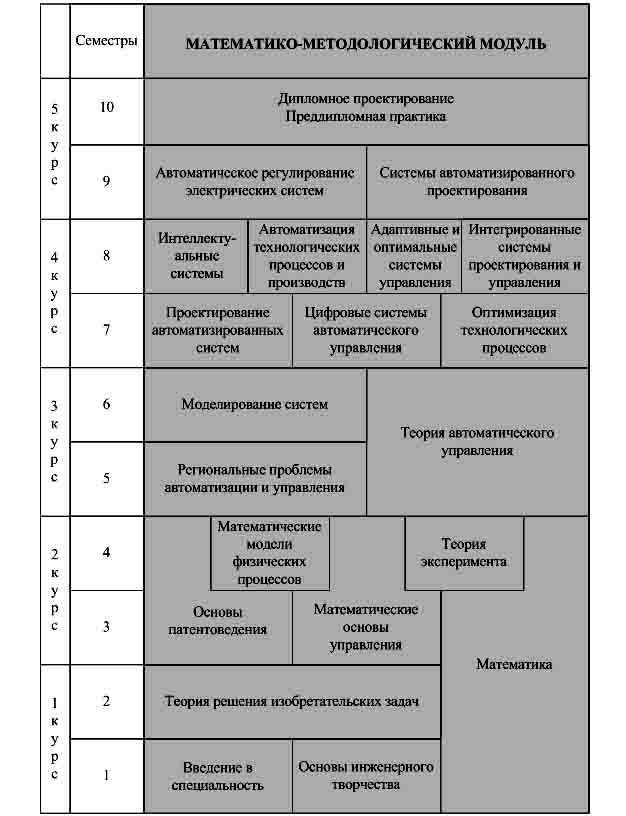
Рис. 2. Структура математико-методологического модуля по направлению «Автоматизация и управление».

Выполнение самостоятельных работ по комплексному анализу технологических объектов управления на основе трёх подходов позволяет рассмотреть во взаимосвязи все особенности объектов управления и технологических процессов, протекающих в них, изучить их принцип действия.

Энергетический подход позволяет выявить механизм преобразования энергии, количества вещества и количества движения, раскрыть принцип действия основных объектов управления, свойственных данной специальности, дать оценку их эффективности, определить требования к системе управления. Он является основой взаимосвязи математико-методологической и технико-технологической компонент, первой ступенькой при построении математических моделей объектов управления.

Математические модели основных технологических процессов имеют вид конечных, дифференциальных, интегральных или интегрально-дифференциальных уравнений. Основой энергетического подхода и теоретическим фундаментом при построении ММ технологических процессов являются основные законы сохранения субстанции (массы М, энергии Э и импульса Д), термодинамического равновесия, переноса субстанции [2].

Рассмотрение на базе системного подхода каждого технологического объекта управления как элемента автоматизированной системы управления позволяет, прежде всего, определить свойства каждого элемента и требования к ним. С одной стороны каждый компонент рассматривается как составная часть единой автоматизированной системы, с другой – как элемент, являющийся объектом изучения в данной специальности. Это позволяет определить задачи по детальному изучению основных физических явлений, составляющих основу технологических процессов, математическому описанию объектов управления как единого целого.

Рассмотрение всех компонентов как взаимосвязанной системы элементов с одной стороны позволяет детализировать и углублённо изучить составные части всех элементов и в том числе технологических процессов – физические явления, математические составляющие общих моделей систем. С другой стороны, такой подход позволяет уяснить требования, цели и задачи отдельных дисциплин в формировании общего знания по специальности, способствует выработке познавательной мотивации к обучению.

Анализ технологических процессов и самого процесса обучения как объекта управления и автоматизации на базе принципов прямой причинно-следственной связи с учётом системных свойств и особенностей преобразования энергии, количества движения и вещества даёт возможность представить каждый элемент и систему в целом с позиций управления и освоить методологию построения математических моделей, как отдельных элементов, так и систем управления в целом.

Дисциплины «Основы инженерного творчества», «Теория решения изобретательских задач» направлены на формирование знаний по методологии инженерного творчества и решению изобретательских задач. Сконцентрированы на развитии творческой атмосферы при обучении, организации учебного процесса как созидательного процесса достижения определённых целей и решения творческих задач.

Методология преподавания математики основывается на двух аспектах. С одной стороны математика направлена на изучение и развитие общих основ самой математики и опирается на собственную методологию. С другой, – математика играет роль языка науки. Обеспечивает представление знаний в компактной формализованной форме, являясь основой анализа, синтеза, моделирования и проектирования систем, отражает её прикладной характер.

Математика, как элемент общей математико-методологической компоненты, сориентирована на комплексное детальное изучение и освоение ключевых математических объектов, методов, приёмов и техники преобразования и решения математических задач с учётом прикладных особенностей специальности. Поэтому ключевым при преподавании математики является использование комплексной методологии с опорой на прикладные особенности специальности с подчинением совокупности методов освоения общих теоретических положений математического аппарата единой целостной методологии специальности.

Центральным на второй ступени профессиональной подготовки по математико-методологической компоненте вектора знаний является дисциплина “Математические основы управления”. Именно в этой дисциплине сконцентрированы основные виды моделей, изучаются методы их взаимного преобразования. Здесь проявляется характерная особенность второй ступени познавательного процесса – постепенный переход от детализации к обобщению. На базе отдельных звеньев, математических моделей различных классов и форм записи строятся обобщённые математические модели систем. Совокупность самостоятельных заданий, принятая на первой ступени усложняется и обобщается на единой платформе специальности. Детализация на этом этапе выражается в детальном изучении различных форм математических моделей и методов их взаимного преобразования, а обобщение – в использовании при построении математических моделей конкретных разнородных систем единых обобщённых математических моделей.

Ключевым здесь является обобщение различных групп и форм математических моделей применительно к конкретным исследованиям по всем дисциплинам специальности, отражающим особенности специальности. Развитие и применение обобщённых математических моделей и методологии применительно к физическим процессам и конкретным научным исследованиям на этой познавательной ступени концентрируется в дисциплинах «Математические модели физических процессов» и «Теория эксперимента». На второй ступени познавательного процесса происходит переход от математического описания отдельных физических явлений к обобщённым математическим моделям совокупности физических явлений, составляющих технологические процессы.

Дисциплина «Теория эксперимента» в совокупности с курсом «Математические модели физических процессов» развивает на базе теории подобия, дисперсионного и корреляционно-регрессионного анализа, теории многофакторного эксперимента методологические навыки и культуру конкретных исследований с использований общих методологических принципов и математических моделей.

Дисциплина «Основы патентоведения» закрепляет навыки и методологию разработки новых технических решений. Совершенствует и поддерживает творческую составляющую профессиональной подготовки и подготавливает обучающихся к проведению сложных научных исследований. На этой ступени профессионального обучения завершается изучение дисциплины «Математика», и одновременно развиваются математические методы применительно к объектам специальности, что отражает наряду с детализацией и обобщением особенности специализации.

Третья ступень включает в качестве базовых для математико-методологической компоненты вектора знаний дисциплины «Теория автоматического управления» и «Моделирование систем». Совокупность самостоятельных и курсовых работ, реализованных на первых двух ступенях, обобщается при выполнении курсовых и самостоятельных работ по дисциплине «Теория автоматического управления». Здесь система заданий, сформированная на первой ступени и развитая на второй, преломляется к исследованию дискретных систем управления. Курсовая работа по этой дисциплине – развитие самостоятельной и курсовых работ по дисциплинам «Математические основы управления», «Управляемые вентильно-электромеханические системы». Результаты построения и идентификации математических моделей вентильно-электромеханических систем на базе принципов и форм математических моделей, изучаемых в курсе «Математические основы управления», используются в курсовой работе по дисциплине «Теория автоматического управления» на третьей ступени при синтезе систем управления.

В дисциплине «Моделирование систем» обобщаются математические модели систем управления применительно к исследованию реальных систем управления технологическими процессами, изучаемыми в дисциплине технико-технологического модуля «Технологические процессы и производства». На основе общей методологии исследования в курсе «Региональные проблемы автоматизации и управления», обобщающего все компоненты вектора знаний, конкретизируются основные компоненты вектора знаний применительно к разработке и внедрению автоматизированных систем управления на базе основных объектов автоматизации региона.

Определяющая тенденция обучения на этом уровне – обобщение. Детализация проявляется на уровне детального исследования технологических процессов и физических явлений, используемых в основных объектах управления. Специализация выражается в конкретизации математических моделей и методов исследования к реальным объектам и системам управления специальности.

Четвёртая ступень познания, соответствующая четвёртому курсу и объединяющая седьмой и восьмой семестры обучения (рис. 3.2), по уровню подготовки соответствует плавному переходу от обобщения к специализации. На этой ступени в математико-методологической компоненте следует выделить три направления.

В соответствии с первым направлением методология и методы анализа и синтеза, изучаемые на третьем курсе, математические модели «Вход – выход» и «Вход – состояние – выход», составляющие основу методов моделирования, анализа и синтеза для всех классов систем, на четвёртой ступени профессиональной подготовки развиваются применительно к цифровым, адаптивным, оптимальным и интеллектуальным системам управления. Эта составляющая обеспечивает преемственность и совершенствование познаний обучающегося в теории систем управления и автоматизации.

Вторая составляющая включает вопросы совершенствования знаний методологии и математических моделей по оптимизации технологических процессов, что реализуется на этой ступени в дисциплинах «Оптимизация технологических процессов», «Автоматизация технологических процессов и производств».

Третье направление связано с освоением обучающимися математических моделей и методологии проектирования автоматизированных систем управления. Основные дисциплины, обеспечивающие эту составляющую на четвёртой ступени:

·   «Проектирование автоматизированных систем управления».

·   «Интегрированные системы проектирования и управления».

Совокупность всех трёх ингредиентов составляет математико-методологическую компоненту четвёртой ступени, ориентированную на углубление знаний, как теории систем управления, так и методов их проектирования, а также методов оптимизации и оптимального управления.

Детализация на этой ступени проявляется в детальном изучении элементов оптимального проектирования и управления, обобщение – в развитии общих методов и моделей применительно к исследованию оптимальных, адаптивных, интеллектуальных систем. Специализация состоит в ориентации всех изучаемых методов и моделей на решение задач управления и проектирования для объектов специальности.

Завершающая ступень в профессиональной подготовке специалиста – пятый курс объединяет все компоненты вектора знаний в единую систему, ориентированную на заданную специальность. Определяющей тенденций в подготовке специалистов на этом этапе является «специализация». Здесь все три направления математико-методологической компоненты вектора знаний интегрируются во всех дисциплинах, изучаемых в девятом семестре, инженерно-производственной и преддипломной практиках, дипломном проектировании.

Дисциплина «Системы автоматизированного проектирования» обобщает знания, полученные на предыдущих ступенях, и, прежде всего по проектированию систем, полученные обучающимися в дисциплинах «Проектирование автоматизированных систем управления» и «Интегрированные системы проектирования и управления» с учётом специальности. В этом одновременно проявляется и обобщение и специализация.

Общие принципы и методология специальности детализируется для решения основных проблем специальности в дисциплинах «Автоматическое регулирование электрических систем», «Автоматизация оперативных процессов в энергосистемах», «Автоматическое регулирование электрических систем», «Автоматизация оперативных процессов и производств», «Автоматизированные системы учёта энергии и мощности в энергосистемах», «Телемеханические системы».

Материалы курсовых работ и проектов, научно-исследовательских работ, докладов на конференциях и статей, результаты прохождения практик интегрируются в единую систему и составляют основу дипломного проекта.

Все составляющие «Детализация», «Обобщение», «Специализация» и все компоненты вектора знаний на завершающей ступени интегрируются в общее знание специальности.

Литература

1. Прошин И.А., Прошин Д.И., Прошина Р.Д. Концепция профессиональной подготовки по вектору знаний / Журнал научных публикаций аспирантов и докторантов. – Курск. – 2009. – № 2. – С. 66 – 70.

2. Математическое моделирование и обработка информации в исследованиях на ЭВМ / И. А. Прошин, Д. И. Прошин, Н. Н. Мишина, А. И. Прошин, В. В. Усманов; Под ред. И. А. Прошина. – Пенза: ПТИ, 2000. – 422 с.

3. Прошин И.А., Прошин Д.И., Прошина Н.Н. Структурно-параметрический синтез математических моделей в задачах обработки экспериментально-статистической информации. – Пенза: Изд-во Пенз. гос. технол. акад., 2007. – 178 с.

Поступила в редакцию 16.03.2008 г.