Использование стохастических сетей процессов с «нетрадиционной» моделью узла в имитационно-математическом моделировании деятельности высшего учебного заведения

 

Тимошин Пётр Александрович,

начальник отдела по научно-исследовательской и воспитательной работе Департамента научных исследований Московской финансово-промышленной академии.

 

Основа концепции имитационного инструментария, с помощью кото­рого можно проводить структурный анализ и имитационное моделирова­ние, заключается в механизмах, которые позволяют агрегировать элемен­тарные процессы и устанавливать между ними функциональные связи (причинно-следственные, информационные, «финансовые» и иные). Ниже предлагается сетевая концепция [4], использующая «удачные» результаты теории стохастических сетей и численные методы, основанные на «диффузной» аппроксимации процессов массового обслуживания. Пока­зано, что аналитические решения в рамках предложенной концепции при­емлемы, но анализ катаклизмов в случае управления рисками затруднен.

Однако эта концепция разработана, в первую очередь, для последую­щей реализации имитационных механизмов в рамках специального пакета имитационного моделирования. Она предназначена для верификации рабо­тоспособности пакета, для оценочных расчетов при отладке имитационных моделей, но не предназначена для практических расчетов показателей рис­ка по аналитическим формулам.

Идею предлагаемой концепции рассмотрим на примере из конкретного проекта «Открытое образование» (см. «е-образование» в [9, 10, 12]).

Учебные процессы в открытом образовании. Учебный процесс - это понятие, охватывающее всю учебную деятельность классического универ­ситета. Учебный процесс состоит из многих компонент: процесса обучения студента по конкретной специальности в течение 5 лет, семестрового учеб­ного процесса на потоке, процесса изучения дисциплины. Классический университет имеет жесткий избыточный набор ресурсов, который позволя­ет реализовать учебный процесс в любой его интерпретации. Однако такой фиксированный набор приводит к издержкам планирования, к удорожанию обучения студента, - без гарантий высокого качества.

В открытом образовании работают специалисты, имеющие квалифи­кацию не ниже, чем в классическом университете. Единственное, что их различает, - это различные образовательные технологии (классическая и комплексная).

В системе открытого образования ресурсы используются в распреде­ленном режиме. Ресурсы распределенного института можно поделить на два типа: интеллектуальный ресурс («учитель») и учебный ресурс (далее ­просто «ресурс»).

Учителя («псевдопроцессоры», активные ресурсы) - это преподавате­ли кафедр, тренеры учебно-тренировочных фирм, тьюторы-консультанты. Учителя предметно относятся к разным распределенным кафедрам через механизм «аттестации».

Ресурсы - это комплекты учебно-практических пособий, студии (если есть дистанционная фаза типа «телеконференции»), режимы Интернет-доступа, аудитории (если есть очная фаза), и другие, без которых обучение студента может не состояться.

Процессом изучения дисциплины (далее - процессом) в распреде­ленном институте назовем неделимую функцию освоения дисциплины студентом по утвержденной программе. Для реализации процесса необхо­димы различные ресурсы.

Процесс «запущен», если возникла необходимость изучения дисцип­лины и распределенный институт имеет для этого ресурсы. Запуск процес­са не означает, что в любой момент времени будет хотя бы один студент, изучающий эту дисциплину. Соответственно, процесс может быть снят (или «отменен»).

Далее будем полагать, что распределенный институт ориентирован, прежде всего, на индивидуализацию обучения студента. Поэтому, с учетом случайных явлений, не зависящих от распределенного института, при мас­совом обслуживании студентов возможны технологические задержки: оче­реди к учителям и задержки из-за временной нехватки ресурсов. Возникает задача определения такого числа ресурсов, при котором процесс обучения по конкретной специальности имел бы продолжительность не хуже задан­ной, с учетом технологических задержек.

При реализации обучения по специальности процессы могут иметь причинно-следственные связи. Поэтому можно говорить о том, что они образуют направленный граф. Применение методов сетевого планирования и управления невозможно; основная трудность - это циклы. Циклы возникают по двум причинам: студенты обучаются не по жесткому учебному плану (возможны различные индивидуальные планы), для от­стающих студентов организуется повторное обучение (возврат к пройден­ной ранее, но не защищенной дисциплине, для её более глубокого изуче­ния). С точки зрения пути студента по графу в каждый момент времени он находится в определенном текущем процессе - в узле графа. Процесс, ко­торый «передал» студента в текущий процесс, назовем «производителем», а процесс, который «примет» студента после завершения текущего, назовем «потребителем».

Рассмотрим возможные диаграммы состояний процесса. Ес­ли мощности ресурсов бесконечны, или каждый процесс используется вме­сте с постоянно закрепленными за ним ресурсами, то возможны два со­стояния: ожидание студентов (ЖС) и выполнение процесса изучения дисциплины (ПУ). В состояние ПУ процесс попадает, получив студента от процесса-производителя. После изучения дисциплины студент переходит к процессу-потребителю и попадает в состояние ЖС, если ка­кой-либо производитель не подготовил следующего студента.

В более реальном случае при конечных мощностях гло­бальных ресурсов появляется состояние ожидания ресурса, когда процессу (точнее – студенту в процессе изучения дисциплины) нужны ресурсы (HP).

В условиях реального университета, когда обучение контролируется, а выделение ресурсов и их возвращение осуществляется с помощью процес­сов планирования и распределения ресурсов, то вводится еще два состоя­ния: подготовка к выполнению (ГВ) и завершение выполнения – контрольные мероприятия, экзамены, зачеты (ЭЗ).

Во время ГВ осуществляется планирование ресурсов, а после ЗВ - воз­врат ресурса в распоряжение планирующих и распределяющих процессов. Соответственно, могут возникнуть ситуации, при которых не возникает необхо­димости в незапланированных ресурсах: у студента есть учебный план. Если же возникает потребность в незапланированных ресурсах, то возможны обратные переходы типа ПУНР. Такие переходы могут привести к блокировкам, которые можно разрешить с помощью из­вестных решений «задачи взаимного исключения» (см. [3]).

Организация и взаимосвязь различных компонент системы открытого образования может быть рассмотрена с позиции управления процессами в следующих подразделениях университета:

·                    управления учебной и учебно-методической работой (УУМР), которое имеет дело со всеми ресурсами, относящимися к учебному процессу;

·                    дирекции распределенного университета, которая совместно с территориально-распределенными филиалами университета (партнерами) отве­чает за реализацию учебного плана;

·                    учебно-методологического совета (УМС), который работает при дирек­ции в качестве коллегиального совещательного органа для постоянного совершенствования государственных образовательных стандартов (ГОС), изменяющихся примерно раз в пять лет, и учебного плана, кото­рый совершенствуется ежегодно (в рамках действующего ГОС);

·                    кафедр (распределенных кафедр открытого образования). Кафедры -это обладатели интеллектуального ресурса (профессорско-преподавательского состава, тренеров, тьюторов, аспирантов, докторан­тов и других «учителей»).

Далее перейдем к оценке времени изучения студентами дисциплин учебно­го плана. Время прохождение всех дисциплин учебного плана студентом – это время пребывания заявки в стохастической сети. Заявки в такой сети будем называть словом «транзакт», чтобы отличать от других элементарных заявок.

Транзакт, попадая из одного узла сети (процесс-производитель) в дру­гой узел (процесс потребитель), свидетельствуют о необходимости изуче­ния студентом следующей дисциплины учебного плана. После этого про­цесс-потребитель выводится из состояния ЖС и попадает в состояние ГВ. После выделения ресурсов (HP), выполнения функции (ПУ) и завершения выполнения контрольных мероприятий (ЭЗ) транзакт появляется на выходе узла - «производителя», а процесс возвращается в состояние ЖС. Случай­ный интервал времени, ограниченный моментом выхода процесса из со­стояния ЖС в начале изучения дисциплины и ближайшим моментом попа­дания в это состояние назовем интервалом активности процесса. Дли­тельность пребывания транзакта в соответствующем узле - это интервал активности. Для оценки времени реакции системы открытого образования, реализуемой в рамках распределенного института по учебному плану, не­обходимо уметь рассчитывать значения интервалов активности всех про­цессов, входящих в состав сети.

Оценка интервала активности процесса. Далее построим итерацион­ную процедуру, позволяющую провести соответствующие оценки. Обозна­чим по тексту данного раздела: А - начало очередной итерации; Б - конец очередной итерации.

А. Начало итерации. Пронумеруем N узлов стохастической сети, харак­теризующих конкретный план, индексами j и предположим справедливость допущений:

1)                 нам известны средние значения всех интервалов активности tи_j, j=1,2, …, N (только в каком-то приближении, так как их необходимо рас­считать);

2)                 известны вероятности поступления транзакта из каждого процесса-производителя в любой потребитель ; эти вероятности определяются исходя из параметров набора учебных планов, индивидуаль­ных схем обучения и числа студентов, проходящих через систему открыто­го образования;

3)                 сеть, отображающая конкретный учебный план, является полнодос­тупной с матрицей передач , причем вероятность поступления тран­закта в процесс-потребитель и в течение интервала времени (t, t+∆_t) являет­ся линейной комбинацией с постоянными коэффициентами  вероятно­стей появления заявок на выходах вершин-производителей c номерами j, j=1, 2, …, N.

После таких допущений можно получить среднее время изучения всех дисциплин плана по простой формуле для замкнутых сетей:

,                                                                                                        (1)

где tи_j; - это средняя длительность интервала активности;

- интенсивность запросов на курс с номером j;

- интенсивность поступления потока студентов, желающих обу­чаться по данному учебному плану.

Поэтому для оценки времени выполнения учебного плана необходимо знать средние значения интервалов активности всех процессов.

Для анализа интервала активности необходимо создать «нетрадицион­ную модель» массового обслуживания, (приведенная ниже модель впервые применялась для расчета эффективности системы телекоммуникаций [8]).

Введем условные обозначения параметров временных интервалов:

tж - процесс ждёт студентов (состояние ЖС);

tг - готовится к выполнению (состояние ГВ);

tн - процессу нужны ресурсы (состояние HP);

tп - процесс учёбы (состояние ПУ);

tэ - экзамен, зачет, контрольное мероприятие (состояние ЭЗ);

tр - длительность ожидания запроса в очереди к ресурсу;

tи - длительность интервала активности процесса;

tс - основная составляющая интервала активности tс = tи - tг;

tr - длительность ожидания какого-то ресурса;

to - длительность ожидания первого элемента ресурса;

tq - длительность ожидания последнего элемента того же ресурса;

tс - главная составляющая интервала активности;

ts - длительность обслуживания в очереди к ресурсу;

tv - время ожидания запрошенных элементов ресурса; 

сr - коэффициент вариации времени ожидания ресурса;

cs - коэффициент вариации времени обслуживания в очереди к ресурсу;

са - коэффициент вариации интервала запросов к ресурсу.

На интервале активности процесс может находиться в состояниях ГВ, HP, ПУ и ЗЭ. Будем считать, что ресурсы выделяются во время пребывания в состоянии HP (интервал tн_j), а освобождаются все сразу - в конце интер­вала пребывания в состоянии ЗЭ (по истечении tэ_j,); оба эти интервала - детерминированные величины. Интервал активности равен:

tи_j^(t) = tг_j+ tн_j^(t)+ tп_j^(t)+ tэ_j,

где tн_j^(t) - длительность пребывания в состоянии HP;

tп_j^(t) - длительность пребывания в состоянии ПУ;

(t) - индекс, показывающий случайный характер индексируемой ве­личины;

j - номер процесса, j=1, 2, …, N.

Будем считать, что величины tг_j и tэ_j известны, а интервал tп_j^(t) задан с помощью математического ожидания tп и дисперсии dп . Интервал tп_j^(t) можно определять с помощью одного из трех возможных способов:

1)                 исходя из характеристик распределенного института (головного
университета, осуществляющего открытое образование);

2)                 с помощью хронометрирования;

3)                 если институт осуществляет приоритетное обслуживание для некоторых категорий учащихся, то tп_j^(t) – это цикл обслуживания; методика
определения цикла обслуживания для потоков типа пуассоновского или
группового и формулы для расчетов приведены в работе [1].

Предположим, что в распоряжении института имеется М глобальных ресурсов, используемых при обучении. Мощность каждого ресурса - S_i, элементов, а для выполнения процесса (изучения курса) j предварительно необходимо выделить R_ij элементов каждого ресурса. Причем 0 ≤R_ij ≤S_i, i=1, 2, ..., М, j=1, 2, ..., N.

Поставим в соответствие началу интервала активности момент появле­ния транзакта на входе модельной системы. Этот транзакт попадает на вход «генератора», на каждом i-ом выходе кото­рого через время tг_j появятся порции R_ij заявок, которые равномерно распределяются по S_i очередям. Длительность обслуживания в каждой очереди tr_i^(t) - это интервал времени, начинающийся в момент выделения процессу первого элемента ресурса i из набора свободных ресурсов и за­канчивающийся моментом возвращения всех R_ij элементов в этот набор, то есть каждому ресурсу соответствует свой «менеджер обслуживания» с контролируемой очередью.

Через какойто интервал времени tо_ij^(t) на входе счетчика появится пер­вая удовлетворенная заявка очереди i-го ресурса. После этого проходит еще R_ij –1 случайных интервалов, пока не появятся остальные заявки (каж­дая соответствует одному выделенному элементу). Если считать, что ин­тенсивность освобождения процессами элементов стационарна во времени, то каждый из R_ij –1 интервалов в среднем равен tr/S_i, где tr_i = М[trj(t) tr_i^(t)].

Через время tw_ij^(t) появляется последняя заявка, соответствующая тому, что выделен последний из запрошенных r_ij элементов i-го ресурса. Через время

появится последняя заявка, соответствующая выделению последнего эле­мента из числа запрошенных, после чего учебный процесс выполняется (за время tп_j^(t) и завершается контрольными мероприятиями (за время tэ_j)

Поток заявок, поступающий на вход рассматриваемой модели - неординарный с интенсивностью . Мы не рассматриваем классический учебный процесс классического университета, стоящийся по принципу объединения:

«специальность<=>группа студентов<=>учебный план<=>учебное расписание».

Однако есть две причины, позволяющие предположить о возникнове­нии в режиме открытого образования случайных групп в потоках транзактов:

·                    один студент может привести несколько студентов (а в модели один транзакт может «породить» группу других транзактов);

·                    в учебном плане могут быть циклы.

Сеть процессов, образующих учебный план, - довольно сложная, полнодоступная. Поэтому в практических расчетах будем считать, что поток групп - пуассоновский, а размер группы распределен по обобщенному эрланговскому закону. Поэтому применим гипотезу Л. Клейнрока [6] о независимости: не к потокам заявок сети, а к потокам групп заявок. Коэффициент вариации интервала поступления с_j в групповом потоке такого типа не меньше единицы. Средний размер случайной группы  связан с квадратом коэффициента вариации соотно­шениями:

 и, наоборот, .

При расчете мы получим величины задержек, которые из-за этих до­пущений будут не меньше того, что есть на самом деле, то есть будем про­изводить расчет на худший случай. Сначала определим интенсивность потока, поступающего в одну из S_i, очередей

.

Введем вероятность того, что запрос на выделение элемента поступил от i-го модуля:

.

Размер группы заявок к ресурсу i от модуля j равен . Средний размер группы, поступающей в одну очередь, равен

,

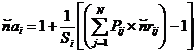Откуда можно получить квадрат коэффициента вариации для потока транзактов, поступающих в i-ю очередь:

.

Составляющая интервала активности tс_j^(t)=tн_j^(t)+tп_j^(t)+tэ_j=tи_j^(t)-tг_j может быть разбита на два слагаемых: интервал пребывания в очереди из-за от­сутствия элементов ресурса tq_j^(t) и интервал времени ts_ij^(t), начавшийся в момент выделения элемента i-го ресурса j-ому модулю и заканчивающийся в момент возвращения в общий набор: tс_j^(t)=tq_j^(t)+ts_ij^(t). Предположим, что нам известна вероятность ненулевой задержки в очере­ди  (в режиме перегрузок) и среднее значение tс_j^(t): tс_j=tи_j-tг_j. По пра­вилу объединения процессов [2] получим среднее время обслуживания в очереди:

.                                                                   (2)

Аппроксимируем функцию распределения времени пребывания в оче­реди выражением

.

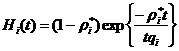Такая аппроксимация позволяет получать дисперсии dq_i с погрешностью, находящейся в пределах 15% даже при эрланговских потоках и постоянных временах обслуживания (см. [7]). Однако при перегрузке (при значениях , близких к единице) это выражение становится практически точным, и можно показать, что распределение числа заявок в очереди при перегрузке - экспоненциальное. Поэтому дисперсия времени пребывания в очереди равна

,                                                                                                  (3)

а средняя длительность задержки в очереди определяется из соотношения, получаемого при аппроксимации процесса изменения длины очереди при перегрузках процессом диффузии

,                                                                                                             (4)

Дисперсии величин dq_i^(t) и dи_j^(t) связаны очевидным соотношением: dи_j=dq_i^(t)+ ds_ij, так как tэ_j - постоянная величина. По правилу получения дисперсии объединенного процесса получим

,                                                          (5)

Определим загрузку элемента  и квадрат коэффициента вариа­ции длительности обслуживания cs_i²=dr_i/tr_i². Далее уточним величину , которую мы считали заданной. При расчете на худший случай, естествен­но, беспокоит задержка в очереди при значениях , близких к единице, то есть в режиме перегрузки.

Дж. Кингман доказал справедливость использования процесса диффу­зии для анализа режима перегрузки [13]. X. Кобаяши попытался эвристи­чески применить формулы, характеризующие решение задачи математиче­ской физики «процесс диффузии с отражающим экраном при наличии те­чения» к расчету параметров стохастических сетей при режимах, далеких от перегрузки, и получил результаты, очень близко совпадающие с резуль­татами статистического моделирования [14, 15]. Е. Геленбе доказал, что применение формул диффузного процесса при расчете средней длины оче­реди дает погрешность, приблизительно равную , где cs_i² - это квадрат коэффициента вариации длительности обслуживания [11], то есть эти формулы дают неплохие результаты в смысле погрешности. В [5 и 14] получена формула для оценки , характерная для больших значений :

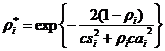.                                                                                       (6)

Благодаря стационарности потока возвращаемых элементов ресурсов, интервал ts_ij^(t) в среднем начинается на середине отрезка, состоящего из R_ij-1 интервалов выделения запрошенных элементов. Поэтому среднее время ожидания R_ij запрошенных элементов

.                                                                                                 (7)

Вероятность того, что величина tv_ij^(t) отлична от нуля, равна
.                                                                                                          (8)

Функцию распределения времени ожидания выделения всех элементов i-го ресурса j-му процессу представим в виде

.

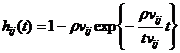Погрешность при такой аппроксимации невелика из-за наличия перегрузки и суперпозиции потоков заявок, проходящих через каждую очередь. Функ­цию распределения величины

по определению записываем в виде

,

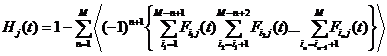где F_ij=1-h_ij(t).

Далее по определению математического ожидания и дисперсии полу­чаем

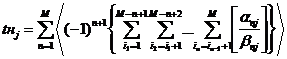                                                          (9)

и

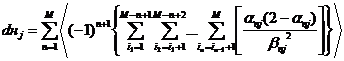,                                          (10)

где для «разгрузки формул» введены вспомогательные переменные

и .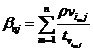

Б. Конец итерации. При построении временной диаграммы получаем:

tи_j=tг_j+tн_j+tп_j +tэ_j,

dи_j=dн_j +dп_j.

Уточнив соответствующие значения, известные в начале итерации с какой-то погрешностью, итерацию можно повторить, и т.д., пока процесс не сойдется к результатам с приемлемой точностью. Таким образом, мето­дом последовательных приближений можно получить интересующие нас параметры интервала активности.

Предлагаемый аппарат описания процессов в узлах стохастической сети распространяется на более широкую предметную область. На его основе создан имитационный инст­рументарий, работающий с потоками различных видов (материальными, информационными денежными. Предло­женные выше формулы предназначены для предварительных оценок сред­них величин. Реальные параметры процессов и показатели рисков измеря­ются в имитационной модели.

 

Литература

 

1.                  Артамонов Г.Т. Анализ производительности ЦВМ методами теории массового обслуживания. – М.: Энергия, 1972. – 176 с.

2.                  Байцер Б. Архитектура вычислительных комплексов. Том 1. – М.: Мир, 1975. -297 с.

3.                  Дийкстра Э. Взаимодействие последовательных процессов. Под ред. Ф. Женюи. – В кн.: Языки программирования. – М.: Мир, 1972, с 9-86.

4.                  Емельянов А.А. Модель функционирования распределенного университета в режиме массового обслуживания. – В кн.: Системный анализ в образовательной и экономической деятельности. – М.: Международная академия открытого образования, 2000, с. 11-23.

5.                  Емельянов А.А., Тарасова Е.В. «Нетрадиционные» методы анализа сетей массового обслуживания. – В кн.: Системный анализ в образовательной и экономической деятельности. – М.: Международная академия открытого образования, 2000, с. 132-150.

6.                  Клейнрок Л. Коммуникационные сети. Стохастические потоки и задержки сообщений. – М.: Наука, 1970. – 255 с.

7.                  Липаев В.В., Колин К.К., Серебровский Л.А. Математическое обеспечение управляющих ЦВМ. – М.: Сов. радио, 1972. – 214 с.

8.                  Руднев Ю.П., Емельянов А.А. Управление сообщениями по линиям связи в сети телеобработки. – В кн.: Однородные вычислительные системы и среды. Часть 1. – Киев: Наукова Думка, 1975, с. 104-106.

9.                  Classroom link. – In: Instructional media and technologies for learning. – NJ, USA: Prentice Hall Inc., 1996, pp. 5-15.

10.              E-intelligence. The powerto know. – NC, USA: A SAS Institute white paper, 2000. – 9 p.

11.              Gelenbe E. On approximate computer system models. – Journal of the ACM, vol.22, № 2, April 1975, pp. 261-269.

12.              Heinich R., Molenda M., Russel J.D., Smaldino S.E. – In: Instructional media and technologies for learning. – NJ, USA: Prentice Hall Inc., 1996, pp. 31-429.

13.              Kingman J.F.C. The heavy traffic approximation in the theory of queues. Proceedings of the Symposium of Congestion Theory. W.L. Smith and W.E. Wilkinson, Union of North Caroline Press, 1965, Chap. 6, pp. 137-169.

14.              Kobayashi H. Application of the diffusion approximation to queuing networks I: Equilibrium queue distributions. – Journal of the ACM, vol. 21, № 2, April 1974, pp. 316-328.

15.              Kobayashi H. Application of the diffusion approximation to queuing networks II: Nonequilibrium distributions and applications to computer modelling. – Journal of the ACM, vol. 21, № 3, July 1974, pp. 459-469.

 

Поступила в редакцию 18.08.2010 г.