Методика классификации
массивов дискретных данных большой длины
Тверетин Алексей Александрович,
соискатель Самарского
государственного технического университета, заместитель директора по внедрению ООО
«Системы управления бизнесом».
1.
Введение и постановка задачи
В настоящее время в связи с лавинообразным
ростом информации, широко применяются системы глубинного анализа данных (data mining) [2]. Эти системы позволяют
анализировать большие массивы данных и решать такие задачи как: регрессия,
поиск ассоциативных правил и другие. Как правило, системы глубинного анализа
данных оперируют с базами данных ERP
(enterprise
resource
planning,
корпоративное планирование ресурсов) [5] , CRM (customer relationship
management system, система управления взаимодействием
с клиентами) [4] и других. Современные системы глубинного
анализа данных содержат стандартный конечный набор простых алгоритмов,
например, методы «наивного» байеса, метод опорных векторов и другие, и
различаются лишь технической реализацией. В частности, такие системы обладают
возможностью решения задачи классификации данных, что необходимо при решении
множества практических задач.
Для решения задачи классификации широкое
распространение получили классификационные правила, главным образом, из-за
наглядности получаемых результатов [1]. Анализ данных с малым числом признаков с
помощью систем глубинного анализа данных технически не составляет труда. При
росте количества признаков на практике возникают проблемы применения таких
систем, так как данные представляются в виде столбцов таблиц или представлений
реляционных баз данных. Еще одной сложностью является природа данных в ERP, CRM и подобным им системам. Их особенностью
является наличие резких всплесков, а также небольшие сдвиги сравниваемых
последовательностей относительно друг друга, что делает трудным использование
корреляционного анализа. Также обычно наблюдается большая протяженность последовательностей,
что при наличии резких всплесков делает трудным использование спектральных методов,
из-за сложности выбора гармоник. К тому же, должна достигаться высокая скорость
обработки информации и экономия вычислительных ресурсов.
Описанные выше проблемы предлагается решить с
помощью предварительного уменьшения признаков, т.е. с помощью сжатия
анализируемых последовательностей. Очевидно, что в этом случае перспективным
видится применение спектрального анализа. Переход в частотную область дает
множество преимуществ для анализа [3]. Но данный подход имеет ряд
недостатков, а именно отсутствие в явном виде структурной информации о сигнале,
а так же, выбор гармоник, что нежелательно, так как может теряться важная
информация при резких всплесках значений данных.
Таким образом, представляется актуальным
разработка методики классификации дискретных последовательностей большой длины
с учетом вышеперечисленных требований, которая могла бы быть использована вместе
с широко распространенными алгоритмами классификации.
2.
Разработка методики
Дискретные последовательности, характеризующие
некие процессы, протекающие в анализируемых системах, можно представить как
случайный сигнал ![]() . Реализация такого сигнала может быть записана как
. Реализация такого сигнала может быть записана как ![]() , где
, где ![]() - амплитуда,
- амплитуда, ![]() - частота,
- частота, ![]() - случайная начальная фаза, кратная дискретности отсчетов.
Важным свойством сигналов является то, что сигнал изначально имеет цифровой
характер, то есть он квантован по частоте и по уровню. Основной сложностью при
анализе таких данных является характер этой зависимости.
- случайная начальная фаза, кратная дискретности отсчетов.
Важным свойством сигналов является то, что сигнал изначально имеет цифровой
характер, то есть он квантован по частоте и по уровню. Основной сложностью при
анализе таких данных является характер этой зависимости.
Предложенная методика состоит из шести этапов:
1)
кодирование качественных характеристик;
2)
дополнение последовательности нулями до
длины ![]() ;
;
3)
вычисление спектров последовательностей;
4)
вычисление признака классификации в виде
значения ![]() ;
;
5)
формирование классификационных правил;
6)
вычисление условной вероятности правила.
Первый этап методики необязателен и используется
только в случае, если элементами дискретной последовательности являются
качественные значения.
Второй этап применяется, поскольку предложенная
базисная комплексная система импульсных функций для сжатия определяется на
множестве ![]() . Она может быть записана как:
. Она может быть записана как: ![]() , где
, где
![]() - номер гармоники анализируемого
сигнала.
- номер гармоники анализируемого
сигнала.
Третий этап заключается в формировании
амплитудно-частотного спектра анализируемого дискретного сигнала ![]() [6], который вычисляется в соответствии с выражением
[6], который вычисляется в соответствии с выражением
![]() , где
, где ![]() . Выражение
. Выражение ![]() есть сумма значений:
есть сумма значений: ![]() . Выражения
. Выражения ![]() и
и ![]() определяются
как:
определяются
как: 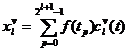 ,
, 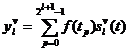 , где
, где ![]() - значение анализируемой последовательности в точке
- значение анализируемой последовательности в точке ![]() , где
, где ![]() . Функции
. Функции ![]() и
и ![]() определяются как:
определяются как: ![]() для нулевой гармоники
для нулевой гармоники ![]() . В случае, если
. В случае, если ![]() и изменяется от 0 до
и изменяется от 0 до ![]() с шагом
с шагом ![]() , функции записываются как:
, функции записываются как: ![]() ,
, ![]() , где
, где ![]() . Сдвигаемые опорные импульсные функции формируются на основе
вспомогательных функций
. Сдвигаемые опорные импульсные функции формируются на основе
вспомогательных функций ![]() и
и ![]() , их можно записать как:
, их можно записать как:![]() и
и ![]() . Количество сдвигов можно определить как
. Количество сдвигов можно определить как ![]() , где
, где ![]() - позиция первого
подинтервала, с которого начинается сдвиг.
- позиция первого
подинтервала, с которого начинается сдвиг.
На четвертом этапе
вычисляется значение евклидова расстояния 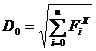 спектров анализируемых
последовательностей, где
спектров анализируемых
последовательностей, где ![]() . На данном этапе
количеству переменных вектора
. На данном этапе
количеству переменных вектора ![]() , которые представляют собой значения отсчетов дискретного сигнала
, которые представляют собой значения отсчетов дискретного сигнала ![]() ставится
в соответствие вектор
ставится
в соответствие вектор ![]() , который
представляет собой значения
, который
представляет собой значения ![]() , где
, где ![]() .
.
Пятый этап заключается
в расчете условной вероятности принадлежности спектра реализации исследуемого
сигнала, к тому или иному классу. Вероятность того, что некоторый спектр ![]() из множества спектров реализаций исследуемого дискретного сигнала
из множества спектров реализаций исследуемого дискретного сигнала ![]() относится к классу
относится к классу ![]() (т.е.
(т.е. ![]() ), можно записать как
), можно записать как ![]() . Событие, соответствующее равенству независимых переменных определенным
значениям, обозначается как
. Событие, соответствующее равенству независимых переменных определенным
значениям, обозначается как ![]() , а вероятность его наступления
, а вероятность его наступления ![]() . Рассчитывается условная вероятность принадлежности спектра
к
. Рассчитывается условная вероятность принадлежности спектра
к ![]() , при равенстве его независимых переменных определенным
значениям. Из теории вероятности известно, что ее можно вычислить по формуле:
, при равенстве его независимых переменных определенным
значениям. Из теории вероятности известно, что ее можно вычислить по формуле: ![]() . Другими словами формируются правила, в условных частях
которых сравниваются все независимые переменные с соответствующими возможными
значениями. В заключительной части выражения присутствуют все возможные
значения зависимой переменной: если
. Другими словами формируются правила, в условных частях
которых сравниваются все независимые переменные с соответствующими возможными
значениями. В заключительной части выражения присутствуют все возможные
значения зависимой переменной: если ![]() , тогда
, тогда ![]() .
.
Шестой этап состоит в том, что для каждого из правил
по формуле Байеса определяется его вероятность на некой обучающей выборке
значений. Предполагая, что независимые переменные принимают значения независимо
друг от друга, выразим вероятность ![]() через произведение
вероятностей для каждой независимой переменной:
через произведение
вероятностей для каждой независимой переменной: ![]() . Тогда вероятность для всего правила можно определить по
формуле:
. Тогда вероятность для всего правила можно определить по
формуле: 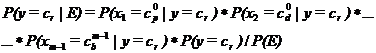 .
.
Вероятность принадлежности спектра к классу ![]() при условии равенства его переменной
при условии равенства его переменной ![]() некоторому значению
некоторому значению ![]() определяется по
формуле:
определяется по
формуле: ![]() и
и ![]() , то есть равно отношению количества расстояний реализаций
сигнала в обучающей выборке, у которых
, то есть равно отношению количества расстояний реализаций
сигнала в обучающей выборке, у которых ![]() и
и ![]() к количеству
расстояний реализаций, относящихся к классу
к количеству
расстояний реализаций, относящихся к классу ![]() .
.
3.
Выводы
Разработанная методика позволяет
классифицировать дискретные последовательности большой длины, используя сжатие
в ![]() раз. Кроме этого,
спектр
раз. Кроме этого,
спектр ![]() инвариантен к сдвигам
и зависит от самых небольших изменений сигнала, что позволяет хорошо выделить
структурные особенности данных. Малая
трудоемкость предварительного сжатия информации делает возможным быструю
обработку данных, что создает предпосылки для разработки практической
реализации методики на основе простых систем глубинного анализа данных, что
позволит проводить классификацию последовательностей, характеризующих любые
временные процессы, в том числе и для решения задач прогнозирования.
инвариантен к сдвигам
и зависит от самых небольших изменений сигнала, что позволяет хорошо выделить
структурные особенности данных. Малая
трудоемкость предварительного сжатия информации делает возможным быструю
обработку данных, что создает предпосылки для разработки практической
реализации методики на основе простых систем глубинного анализа данных, что
позволит проводить классификацию последовательностей, характеризующих любые
временные процессы, в том числе и для решения задач прогнозирования.
Литература
1.
Барсегян А.А. Методы и модели
анализа данных: OLAP и Data Mining. - СПб: БХВ-Петербург, 2004. — С. 67-128.
2.
Белов В.С.
Информационно-аналитические системы. Основы проектирования и применения:
учебное пособие, руководство, практикум. - М: Московский государственный
университет экономики, статистики и информатики, 2000. - С. 85-86.
3.
Гольденберг Л.М., Матюшкин Б.Д., Поляк
М.Н. Цифровая обработка сигналов: Учеб. Пособие для вузов. - М.: Радио и связь,
1990. – С.123-143.
4.
Елашкин М.
SAP Business One. Строим эффективный бизнес. – М.: КУДИЦ-ПРЕСС,
2007. – С.105-109.
5.
Рыбников А.И. Система управления предприятием
типа ERP.
– М.: Азроконсалт, 1999. – 214 с.
6.
Тверетин А.А. Сравнение конкатенированных
данных на основе их спектральных характеристик // Современные наукоемкие
технологии. – Москва, 2008. - №6. – C. 34-39.
Поступила в редакцию 11.08.2010 г.