Выбор параметров настройки обратной связи адаптивной системы управления с эталонной моделью по расширенной АФХ

 

Пугачев Василий Иванович,

доцент кафедры автоматизации производственных процессов Кубанского государственного технологического университета.

 

Рассмотрены особенности расчета параметров обратной связи систем управления с эталонной моделью. Показано, что аппроксимация звена чистого запаздывания рядом Паде точнее, чем рядом Тейлора. Доказана эффективность использования расширенной амплитудно-фазовой характеристики при определении параметров звена обратной связи.

 

Для управления объектами с переменными параметрами в [1-3] предлагалось использовать адаптивную систему управления с эталонной моделью. Это достигается введением в контур управления модели-эталона, который соединен с основной системой управления.

На рисунке 1 приведена схема включения модели-эталона параллельно объекту.

Выходная координата объекта управления  измеряется и сравнивается с выходным сигналом модели . Разность между ними вводится в цепь обратной связи, выходной сигнал  которой вычитается из управляющего сигнала , действующего на объект.

 

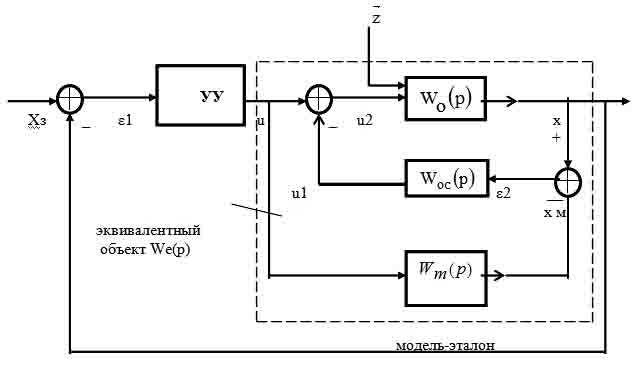
Рис. 1.

 

Такая система обеспечивает ослабление влияния изменения динамических характеристик объекта на динамические характеристики замкнутой системы в целом.

Реализация управления по модели сталкивается с проблемой обеспечения устойчивости эквивалентной модели и всей замкнутой системы управления.

Как подобрать параметры обратной связи, которые обеспечат устойчивость эквивалентной модели при заданном диапазоне изменения параметров объекта.

Ранее [2] было показано, что интегро-дифференцирующее звено наилучшим образом подходит для этой цели. Но как выбрать значение Кос и Тос, чтобы модель была устойчивой?

Для решения данной задачи в [3] применен критерий Гурвица, а чистое запаздывание заменено тремя членами его разложением в ряд Тейлора. При этом приходится иметь дело с определителем высокого порядка и большим числом диагональных миноров, определяющих границу устойчивости. Практика показывает, что использование ряда Паде значительно лучше приближает свойства объекта к реальным, чем ряд Тейлора. В этом легко убедиться, рассматривая рисунок 1.

Пусть

, , ,

.

 

,

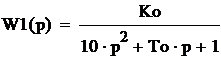его разложение в ряд Тейлора:

,

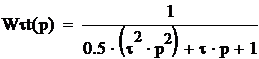Паде: .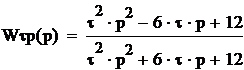

 

, .

Заменивp, получим АФХ объекта с чистым запаздыванием и его аппроксимациями.

 

 

 

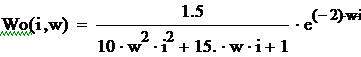
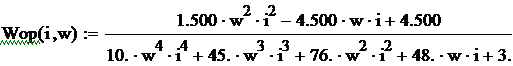
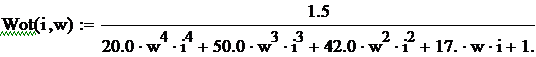
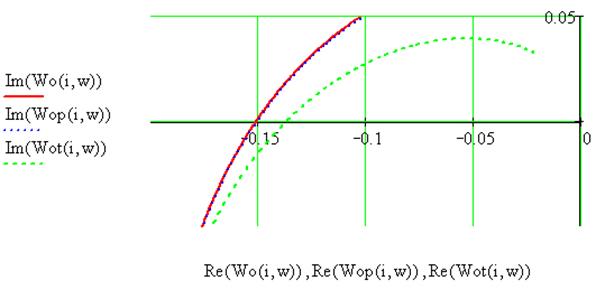
Рис. 2.

 

Как видно из рисунка 2, АФХ объекта с чистым запаздыванием и разложением его в ряд Паде – совпадают, с разложением в ряд Тейлора – существенно отличается, что может привести к недопустимым ошибкам в расчетах параметров обратной связи и неустойчивости эквивалентной модели..

Для исключения необходимости рассмотрения многих условий устойчивости а также необходимости аппроксимации звена чистого запаздывания воспользуемся расширенными амплитудно-фазовыми характеристиками. Попытаемся обеспечить переходной функции эквивалентной модели требуемую относительную степень затухания. Будем рассматривать эквивалентную модель как замкнутую систему, регулятором в которой является звено обратной связи.

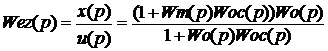                                               (1)

Как следует из выражения (1), устойчивость эквивалентной модели не зависит от свойств самой модели.

Если расширенная АФХ разомкнутой системы пройдет через точку на комплексной плоскости с координатами -1, i0, то переходная функция эквивалентной модели будет обладать требуемой относительной степенью затухания.

Из формулы (1) видно, что передаточная функция разомкнутой системы равна .

Сделаем замену p=(i-m)w в передаточной разомкнутой системы, полученной из эквивалентного объекта, как замкнутой и приравняем -1.

                                                                  (2)

После несложных преобразований получаем:

                                                                 (3)

Равенство (3) будет справедливо, если в нем равны вещественные и мнимые части.

Обозначим: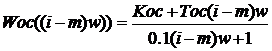,                                     (4)

.                                                      (5)

Мнимые части:, или .

Вещественные части: ,                                           (6)

или:.                                                         (7)

Логично предположить, что исходная модель должна быть по свойствам близка к начальным свойствам реального объекта, однако это усложняет процесс её имитации.

Пусть объект – апериодическое звено второго порядка с запаздыванием. Для простоты выберем в качестве модели – апериодическое звено первого порядка.

 .                                                                                                          (6)

Для нахождения в плоскости параметров Koc и Toc линии близкой к границе устойчивости примем .

, , ,

.

 

 

 

.

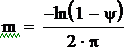Задаваясь значениями частоты, построим линию границы заданной относительной степени затухания для эквивалентной модели, рисунок 3.

 

,

 

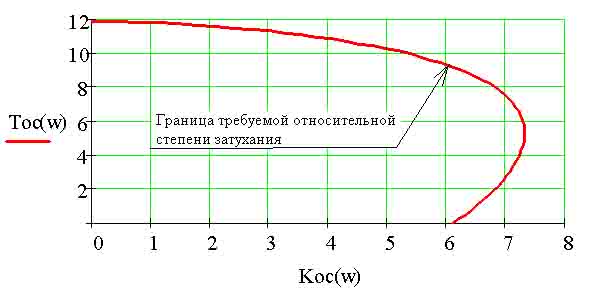
Рис. 3.

 

Наличие дифференцирующей составляющей в обратной связи позволяет увеличивать Кос.

Примем: , .,

_{Посмотрим вид переходных функций реального объекта Ho(t), модели Hm(t) и эквивалентной модели He(t).}

 

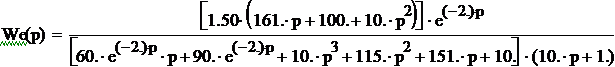
Для построения переходной функции эквивалентной модели, имеющей звено чистого запаздывания, используем обобщенную вещественную частотную характеристику.

_{При наличии звена чистого запаздывания без его аппроксимации переходные процессы в системе следует проводить по обобщенным вещественным частотным характеристикам. Однако, во избежание ошибок, сначала следует проверить систему на устойчивость по критерию Найквиста-Михайлова, рисунок 4.}

 

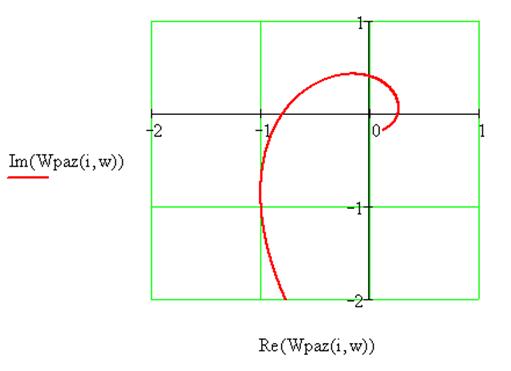
Рис. 4.

 

Как следует из рисунка, эквивалентная модель устойчива

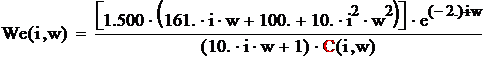
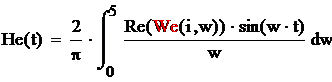
_{Графики переходных функций реального объекта Ho(t), модели Hm(t) и эквивалентной модели He(t) приведены на рисунке 5.}

 

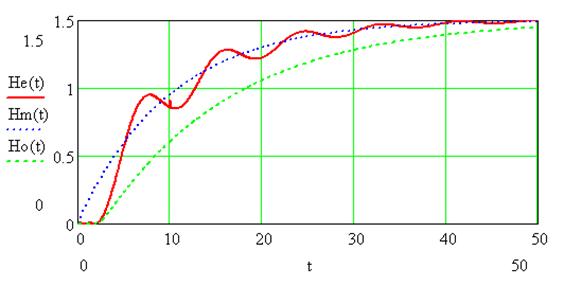
Рис. 5.

 

_{Как следует из графиков переходных функций, эквивалентная модель He(t) стремится воспроизвести переходную функцию модели Hm(t).}

_{Построив амплитудно-фазовую характеристику разомкнутой системы можно убедиться в её устойчивости в замкнутом состоянии и определить запас устойчивости по модулю и фазе. Используя Mathcad [4], легко подобрать желаемые параметры управляющего устройства. Ниже приведены переходные функции замкнутой системы с моделью при различных параметрах объекта.}

Таблица параметров объекта и модели.

 

 

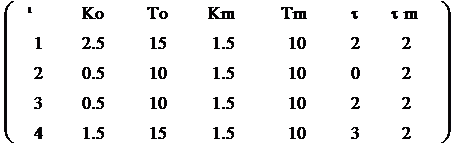
Для каждого из четырех вариантов проверялась устойчивость замкнутой САУ, рисунок 6, после чего строились переходные функции.

, , ,

 

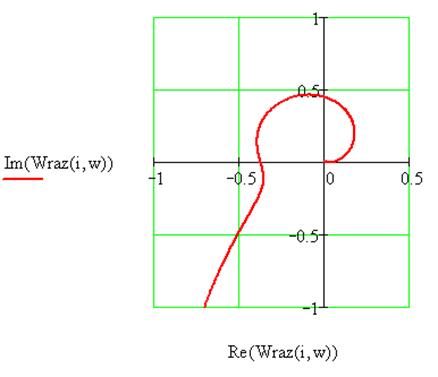
Рис. 6.

 

_{Ниже, на рисунке 7, приведены графики переходных функций, из которых видно, что изменение параметров объекта в широких пределах практически не изменяет динамику замкнутой системы.}

 

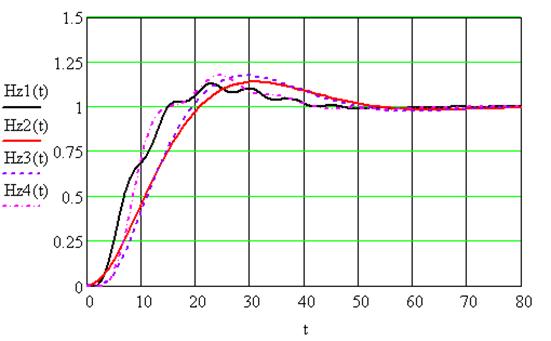
Рис. 7.

 

Выводы

 

1. Ряда Паде по сравнению с рядом Тейлора позволяет более точно рассчитывать амплитудно-фазовую характеристику систем с чистым запаздыванием и находить параметры обратной связи эквивалентной модели.

2. Использование расширенной амплитудно-фазовой характеристики облегчает и упрощает выбор параметров обратной связи систем с эквивалентной моделью.

Расчет переходных процессов в системе с чистым запаздыванием приходится проводить по обобщенным вещественным частотным характеристикам (ОВЧХ), а его разложение в ряд Паде позволяет получать аналитические выражения, графики которых практически не отличаются от построенных по ОВЧХ при исследовании динамики адаптивной системы управления с эталонной моделью.

 

Литература

 

1. Пугачев В.И. Исследование возможностей адаптивной системы управления с эталонной моделью // Изв. Вузов. Пищевая технология. -2007. -№ 2. –С 80-83.

2. Пугачев В.И. Устойчивость эквивалентной модели системы управления с эталонной моделью и объектом третьего порядка // Изв. Вузов. Пищевая технология. -2007. -№ 4. –С 88-91.

3. Пугачев В.И. Влияние чистого запаздывания на устойчивость эквивалентной модели адаптивной системы управления с эталонной моделью // Изв. Вузов. Пищевая технология. -2007. -№ 5-6. –С 76-78.

4. Кудрявцев Е.М. Mathcad 11. Полное руководство по русской версии. – М.: МДК Пресс, 2005. -592 с.

 

Поступила в редакцию 05.03.2010 г.