Прогнозирование состояния технологического процесса

 

Клочков Юрий Сергеевич,

кандидат технических наук, доцент,

Самарский государственный аэрокосмический университет имени С. П. Королева.

 

Так как любой технологический процесс изготовления того или иного размера детали состоит из некоторого количества операций, то качество изготовления размера является величиной зависящей от качества всех операций [Григорович В.Г., 2001].

Разделим все возможное поле значений на три составляющие. Первое будет содержать в себе значения большие, чем +S, второе от +S до –S и третье меньшие чем –S. Значение S возьмем с такой точностью, чтобы не один размер не совпал с границами. Тогда граф состояний технологической операции будет иметь вид.

 

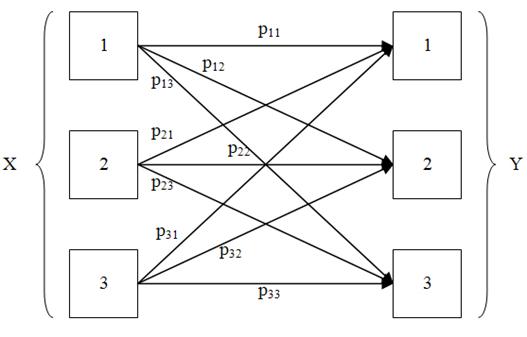
Рис. 1. Граф состояния технологической операции.

 

Награды из акрила

на заказ из акрила, дерева, металла в Москве

parallaks.com

Для определения вероятного числа попадания размера в то или иное поле можно рассчитать по следующим уравнениям:

р'₁=p₁₁р₁+p₁₂р₂+p₁₃р_3;

р'₂= p₂₁р₁+p₂₂р₂+p₂₃р_3;

р'₃= p₃₁р₁+p₃₂р₂+p₃₃р₃.

Если р₁, р₂, р₃ будут зависеть от конкретного случая, то p₁₁,p₁₂,p₁₃ и другие следует определить заранее, т.е. рассчитать матрицу переходных вероятностей.

Pij=

p11 p21 p31

p12 p22 p32

p13 p23 p33

Матрица переходных вероятностей содержит информацию о преобразованиях параметра x заготовки на последующей операции [Григорович В.Г., 2001]. Оптимально настроенной технологической операции соответствует матрица переходных вероятностей, которую можно назвать эталонной. Данную матрицу можно использовать в качестве меры оценки состояния технологического процесса.

С позиции информационной теории управления обеспечение непрерывного технологического процесса автоматизированного производства заключается в поддержке на постоянном заданном уровне информационных потоков, отражающих состояние технологического процесса. Один из таких потоков – взаимная информация, содержащаяся в двух системах.

Для наших расчетов была определена матрица переходных вероятностей, которая постоянно корректируется на протяжении всего производства.

В процессе производства наружного штока гидродомкрата МА 43.0000 (рис. 2), применяемого при ремонтах вертолетного шасси, формирование основных размеров происходит на нескольких операциях, так, например, размер диаметра 155,8 формируется за счет 15 и 45 операций (рис. 3, рис. 4).

 

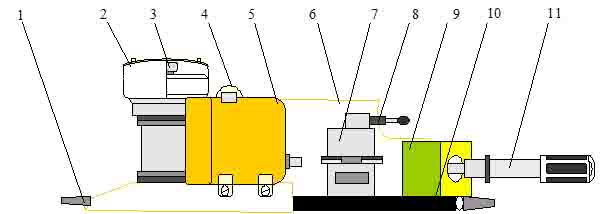
Рис. 2. Гидродомкрат МА-43.

1 – ручка; 2 – колпак; 3 – гидроцилиндр; 4 – заглушка; 5 – гидробак; 6 – кожух; 7 – кран управления 629600ВТ; 8 – рукоятка крана управления; 9 – ручной насос; 10 – основание; 11- рукоятка.

 

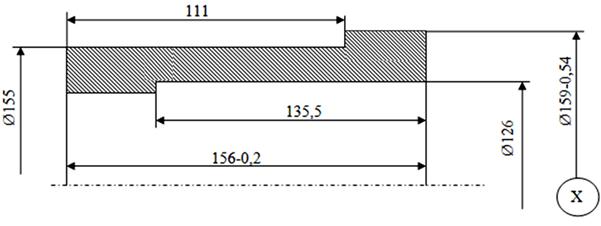
Рис. 3. 15 операция.

 

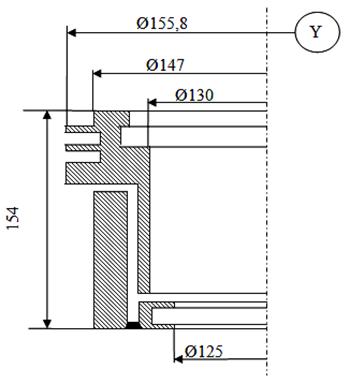
Рис. 4. 45 операция.

 

Параметр Y формируется на двух последовательных операциях механической обработки. В период анализа технологического процесса было установлено, что параметры Х и Y имеют распределение Гаусса с параметрами:

=158,603 (мм); S_x=0,04504; =155,6424 (мм); S_y=0,058504.

Для контроля технологического процесса были выбраны границы контроля:

а_х=–S_x=158,5579;

b_х=+S_x=158,6480;

а_у=–S_y=155,5839;

b_y=+S_y=155,7009.

Вычислим значения функции распределения F(X) и плотности вероятности f(X) в точке Х=а. Принимаем М(Х)= , М(Y)= , σ=S и проводим замену переменных:

t_x=(X-)/ S_x, t_y=(Y-)/ S_y.

При Х=а_х, Y=a_y, t_x= t_y=-1, f(a_x)= f(a_y)=w(1)=0,242, F(a_y)=Ф(-1)=1- Ф(1)=0,159

Здесь w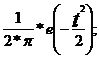(t)= Ф(t)= – интеграл Лапласа [Гмурман В.Е., 2002].

Опытным путем определена матрица оценок переходных вероятностей:

Pij=

0,7 0,2 0,2

0,2 0,7 0,2

0,1 0,1 0,6

для второй операции. Объем выборки n, используемой для получения исходных данных равен 30. На этом подготовка исходных данных заканчивается.

Используя данные, полученные на первой контрольной операции f₁=5; f₂=18, f₃=7 и матрицу оценок переходных вероятностей, найдем f'₁; f'₂; f'₃. Решим систему уравнений:

р'₁=0,7р₁+0,2р₂+0,1р_3,

р'₂=0,2р₁+0,7р₂+0,1р_3,

р'₃=0,2р₁+0,2р₂+0,6р₃,

где р_i =f_i/n.

Для данного примера р₁=0,166; р₂=0,6; р₃=0,233. Результаты решения системы:

р'₁=0,2828; р'₂=0,3163; р'₃=0,3999.

Так как р'_i =f'_i/n, то f'₁=0,2828*30=8,484≈8; f'₂=0,3999*30=11,97≈12; f'₃=0,3163*30=9,489≈10.

Данные, полученные с помощью предлагаемого метода прогнозирования состояния технологических процессов, хорошо согласуются с фактическими данными, полученными в результате контроля.

Оценим точность и стабильность процесса, используя в качестве исходных данных результаты прогнозирования его состояния.

Определяем смещение центра группирования:

ΔY==.

t=;

Так как t<t_{29; 0,05} следовательно, смещение центра группирования размеров не существенно [2].

Оценим значимость изменения дисперсии.

Найдем Н_k(Y)=.

 

Н=0,845.

;

Вывод: так как  F_m;m2;α1, даем окончательное заключение о состоянии технологического процесса. Поскольку изменение центра группирования размеров  и дисперсии S² несущественно, процесс будет находиться в подконтрольном состоянии и разработка корректирующих мер не требуется.

 

Литература

 

1.                  Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов. – 8-е изд., сер. – М.: Высш. шк., 2002. – 479 с.

2.                  Григорович В.Г., Юдин С.В., Козлова Н. О., Шильдин В.В. Информационные методы в управлении качеством. – М.: РИА «Стандарты и качество», 2001. – 208 с.

 

Поступила в редакцию 13.12.2010 г.