Об одной нелокальной краевый задаче для
одного уравнения Буссинеска четвертого порядка
Мехралиев
Яшар Топуш оглу,
кандидат физико-математических наук,
доцент кафедры дифференциальных уравнений, заместитель декана
механико-математического факультета Бакинского государственного университета,
Гардашова
Фарида Расул гызы,
преподаватель строительного колледжа при
Азербайджанском архитектурно-строительном университете.
В работе исследуется нелокальная
краевая задача для псевдогиперболического уравнения четвертого порядка.
Сначала доказывается теорема о едилетвенности классического решения. Далее,
методом разделения переменных строится классического решение в ясном виде.
В области ![]() рассмотрим уравнение
рассмотрим уравнение
![]() (1)
(1)
при обычных локальных граничных
![]()
![]() (2)
(2)
и нелокальных краевых
![]() ,
,
![]() (3)
(3)
условиях, где ![]() заданные числа,
заданные числа, ![]() - заданные функции, а
- заданные функции, а ![]() - искомая функция.
- искомая функция.
Определение. Под
классическим решением задачи (1) – (3) понимаем функции ![]() непрерывного в
замкнутой области ДТ-
вместе со всеми своими производными, входящими в уравнение (1) и удовлетворяющую
всем условиям (1) – (3) в обычном смысле.
непрерывного в
замкнутой области ДТ-
вместе со всеми своими производными, входящими в уравнение (1) и удовлетворяющую
всем условиям (1) – (3) в обычном смысле.
Для изучения вопроса
единственности классического решения задачи важную роль играет следующая
Лемма [2]. Пусть ![]() ,
, ![]() при любом
при любом ![]() и
и ![]()
![]() . Тогда
. Тогда ![]() при любом
при любом ![]() .
.
Теорема 1. Если ![]() , то задача (1) – (3) не может иметь более одного классического
решения.
, то задача (1) – (3) не может иметь более одного классического
решения.
Доказательство.
Доказательство этой теоремы проводится по следующей схеме [1]. Допустим, что
существуют две классических решения рассматриваемой задачи ![]() и
и ![]() . Рассмотрим разность
. Рассмотрим разность ![]() .
.
Очевидно, что функция ![]() . Удовлетворяет однородному уравнению
. Удовлетворяет однородному уравнению
![]() ДТ) (4)
ДТ) (4)
и условиям
![]() , (5)
, (5)
![]()
![]() . (6)
. (6)
Докажем, что функция ![]() тождественно равна
нулю. Для этого умножим обе части уравнения (4) на функцию
тождественно равна
нулю. Для этого умножим обе части уравнения (4) на функцию ![]() и проинтегрируем полученные
равенства по х от 0 до 1:
и проинтегрируем полученные
равенства по х от 0 до 1:
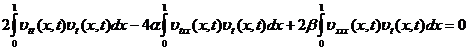 (7)
(7)
Использую граничные условия (5) будем
иметь:
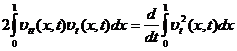 ,
,
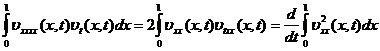 ,
,
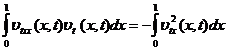 .
.
Тогда из (7) , имеем:
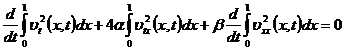 .
.
Примем обозначение
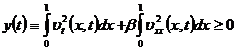 .
.
Очевидно, что
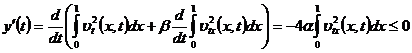 .
.
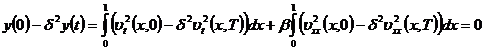 .
.
Таким образом, функция ![]() удовлетворяет всем
условиям леммы. Следовательно, в силу леммы она тождественно равна нулю:
удовлетворяет всем
условиям леммы. Следовательно, в силу леммы она тождественно равна нулю:
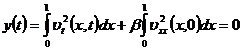 .
.
Из этого тождества заключаем, что
![]() ,
, ![]() .
.
Отсюда получаем
![]()
Теперь же пользуясь нелокальными
условиями (6), будем иметь
![]() .
.
Следовательно, с=0, ибо ![]() . Тем самым доказано, что
. Тем самым доказано, что ![]() .
.
Таким образом, если существуют
два решения ![]() и
и ![]() задачи (1) – (3) , то
задачи (1) – (3) , то ![]() . Отсюда следует, что если решение задачи (1) – (3)
существует, то оно единственное. Теорема доказана.
. Отсюда следует, что если решение задачи (1) – (3)
существует, то оно единственное. Теорема доказана.
Очевидно, что необходимым
условием существования непрерывного в ДТ-
решения является выполнение условии согласования
![]()
![]() .
.
Так как система 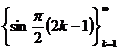 полна в
полна в ![]() , то каждое классическое решение задачи (1) – (3) будем
искать в виде
, то каждое классическое решение задачи (1) – (3) будем
искать в виде
![]() , (8)
, (8)
где ![]()
Применяя метод Фурье, из (1), (3)
получим:
![]() (9)
(9)
![]() ,
, ![]() (10)
(10)
где
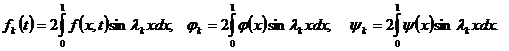
Предположим, что ![]() . Тогда решая задачу (9), (10), находим:
. Тогда решая задачу (9), (10), находим:
![]()
![]()
![]() +
+
![]() (11)
(11)
![]() ,
, ![]()
![]() .
.
Дифференцируя (11) два раза,
получим:
![]()
![]()
![]()
![]() , (12)
, (12)
![]()
![]()
![]()
![]()
![]() (13)
(13)
Нетрудно видеть, что
![]()
![]() ,
,
![]() .
.
Учитывая эти оценки, из (11),
(12), (13) соответственно имеем:
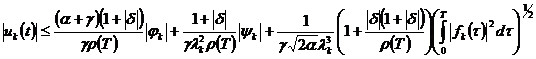 ,
,
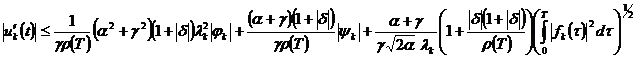 .
.
![]()
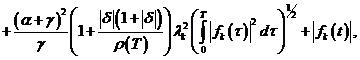
Отсюда имеем:
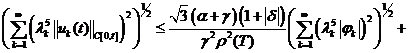
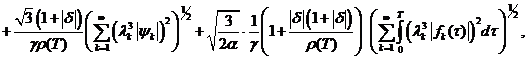 (14)
(14)
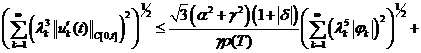
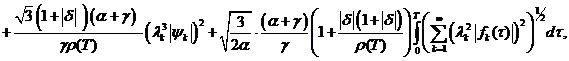 (15)
(15)
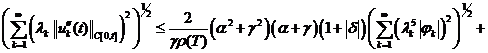
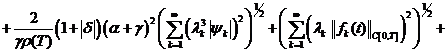
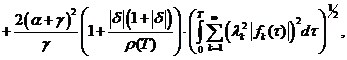 (16)
(16)
Справедлива следующая
Теорема 2. Пусть ![]()
![]() и
и
1. ![]()
![]()
2. ![]()
![]()
3.![]() ,
, ![]()
![]()
Тогда
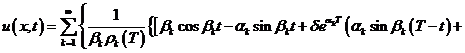
![]()
![]()
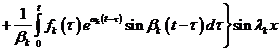 (17)
(17)
является классическим решением
задачи (1) – (3).
Доказательство. Принимая во
внимание условия теоремы 2 из (14), (15) и (16) соответственно получим:
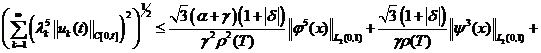
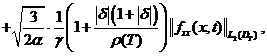 (18)
(18)
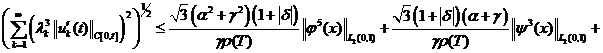
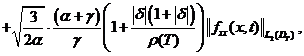 (19)
(19)
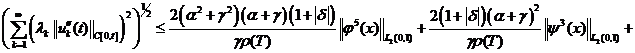
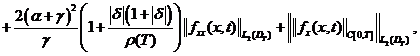 (20)
(20)
Очевидно, что
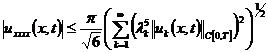 (21)
(21)
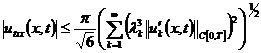 (22)
(22)
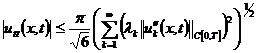 (23)
(23)
Из (21) – (23), с учетом (18) –
(20), следует, что функции ![]()
![]() - непрерывны в ДТ.
Непосредственной проверкой легко видеть, что функция
- непрерывны в ДТ.
Непосредственной проверкой легко видеть, что функция ![]() удовлетворяет
уравнению (1) и условиям (2), (3) в обычном смысле. Теорема доказана.
удовлетворяет
уравнению (1) и условиям (2), (3) в обычном смысле. Теорема доказана.
Литература
1. Смирнов В.И. Курс высшей
математики, Т. V. М.
1957.
2. Мегралиев Я.Т. Об Одной
нелокальной краевой задаче для псевдогиперболического уравнения третьего
порядка // Вестник Бакинского государственного университета, серия физико-математических
наук, 2008, №1, с. 84 – 91.
Поступила
в редакцию 26.02.2010 г.