Об одном способе расщепления некоторых
задач, описываемых уравнением в частных производных параболического типа
Алламуратов
Шарапатдин Зиуатдинович,
соискатель, старший преподаватель
Нукусского государственного педагогического института им. Ажинияза.
Согласно принципу расщепления
отдельные члены (или комплексы), входящие в уравнение, можно реализовать
отдельно, что упрощает построение аналитических и численных решений.
Используем метод расщепления в
двумерной задаче массопереноса при краевых условиях второго рода.
![]()
при t>0
![]()
![]()
где ![]() ε(t)-заданные функции от времени, T,H,a,-известные физические параметры. В
безразмерных переменных данную краевую задачу можно записать в виде
ε(t)-заданные функции от времени, T,H,a,-известные физические параметры. В
безразмерных переменных данную краевую задачу можно записать в виде
![]()
![]()
![]()
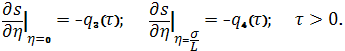
где ![]()
а ![]() и
и ![]() - некоторые константы.
- некоторые константы.
Применим к исходному уравнению
принцип расщепления [1-3].
В результате этого получим
следующую систему.
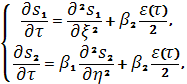
где ![]()
Так как первое уравнение системы
не зависит от ![]() а
второе уравнение ее от
а
второе уравнение ее от ![]() то
выше указанная система равносильна следующей:
то
выше указанная система равносильна следующей:
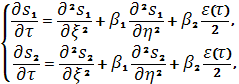
cумма которых равносильна предыдущей системе.
Применим интегральное преобразование Лапласа относительно переменной ![]()
![]()
к данной системе с учетом
начальных и граничных условий.
Тогда придем к следующей краевой
задаче.
![]()
![]()
![]()
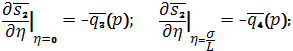
Первое и второе уравнения
исходной системы имеют следующие решения;
![]()
![]()
Здесь ![]() определяется
из граничных условий. Осуществляя обратный переход к действительным функциям,
получим искомое решения.
определяется
из граничных условий. Осуществляя обратный переход к действительным функциям,
получим искомое решения.
Таким образом
двумерная задача по определению искомых функций s1 и s2 сведена к решению одномерных задач,
описываемых уравнениями в частных производных параболического типа.
Численное
решение задач расщепления уравнений теплопроводности и конвективной диффузии
приведены в [1, 2], а аналитическое решение для граничных условиях первого рода
независящих от времени приведены в [3].
Литература
1. Пасконов В.М., Полежаев В.Н.,
Чудов Л.А. Численное моделирование процессов тепло и массообмена. М.: Наука,
1984,- 284 с.
2. Гладкий А.В., Ляшко И.И., Мистецкий
Г.Е. Алгоритмизация и численный расчет фильтрационных схем.-Киев:
Науково думка,1981.-287 с.
3. Баклушин М.Б. Принцип
расщепления для задачи, описываемой уравнением в частных производных
параболического типа. Материалы меж. науч. техн. конф. Современные проблемы и перспективы механики.
Ташкент. 2006.
Поступила
в редакцию 14.05.2010
г.