Об одной нелокальной краевой задаче для уравнения
колебаний стержня
Салимова
Аферим Абдул гызы,
старший методист отдела магистратуры Азербайджанской
государственной нефтяной академии.
В
работе исследуется нелокальная краевая задача для уравнения колебаний стержня.
Сначала доказывается теорема о единственности классического решения. Далее,
методом разделения переменных строится классическое решение в явном виде.
В области ![]() рассмотрим уравнение
[1]
рассмотрим уравнение
[1]
![]() (1)
(1)
и обычных локальных граничных
![]() (2)
(2)
и нелокальных краевых
![]() , (3)
, (3)
условиях, где ![]() - заданное число,
- заданное число, ![]() - заданные функции, а
- заданные функции, а ![]() - искомая функция.
- искомая функция.
Определение. Под классическим решением
задачи (1)-(3) понимаем функцию ![]() , непрерывную в замкнутой области
, непрерывную в замкнутой области ![]() вместе со всеми своими
производными, входящими в уравнение (1) и удовлетворяющую всем условиям (1)-(3)
в обычном смысле.
вместе со всеми своими
производными, входящими в уравнение (1) и удовлетворяющую всем условиям (1)-(3)
в обычном смысле.
Теорема 1. Если ![]() , то задача (1)-(3) не может иметь более одного классического
решения.
, то задача (1)-(3) не может иметь более одного классического
решения.
Доказательство. Доказательство этой
теоремы проводится по следующей схеме [2]. Допустим, что существуют два
классических решения рассматриваемой задачи ![]() и
и ![]() . Рассмотрим разность
. Рассмотрим разность
![]() .
.
Очевидно, что функция ![]() , удовлетворяет однородному уравнению
, удовлетворяет однородному уравнению
![]() (4)
(4)
и условиям
![]() , (5)
, (5)
![]() . (6)
. (6)
Докажем,
что функция ![]() тождественно равна
нулю. Для этого умножим обе части уравнения (4) на функцию
тождественно равна
нулю. Для этого умножим обе части уравнения (4) на функцию ![]() и проинтегрируем
полученное равенство по
и проинтегрируем
полученное равенство по ![]() от 0 до 1:
от 0 до 1:
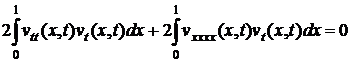 . (7)
. (7)
Используя
граничные условия (5) будем иметь:
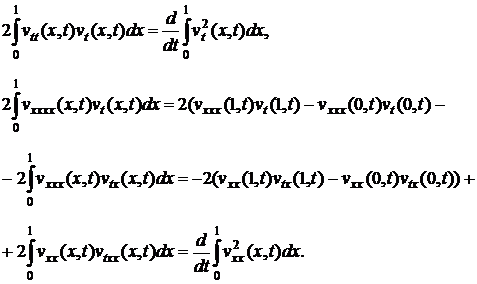
Тогда,
из (7) имеем:
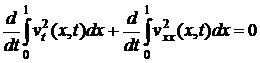
или
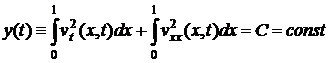 .
.
Отсюда,
с учётом (6), получаем:
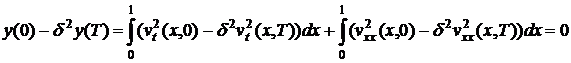 .
.
Таким
образом
![]() .
.
Так как ![]() , то
, то ![]() . Следовательно,
. Следовательно,
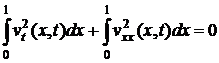 .
.
Из этого тождества заключаем, что
![]() .
.
Отсюда следует
![]() .
.
Теперь же, пользуясь нелокальными
условиями (6), будем иметь:
![]() .
.
Следовательно, ![]() ибо
ибо ![]() .
.
Тем самым доказано, что ![]() .
.
Таким образом, если существуют
два решения ![]() и
и ![]() задачи (1)-(3), то
задачи (1)-(3), то ![]()
![]() . Отсюда следует, что если решение (1)-(3) существует, то оно
единственное. Теорема доказана.
. Отсюда следует, что если решение (1)-(3) существует, то оно
единственное. Теорема доказана.
Очевидно, что необходимым
условием существования непрерывного в ![]() решения является
выполнение условий согласования
решения является
выполнение условий согласования

Так как система 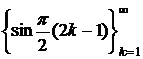 полна в
полна в ![]() , то каждое классическое решение задачи (1)-(3) будем искать
в виде:
, то каждое классическое решение задачи (1)-(3) будем искать
в виде:
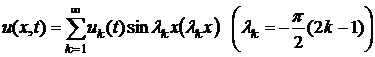 , (8)
, (8)
где
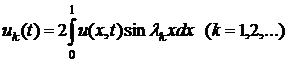 .
.
Применяя
метод Фурье, из (1), (3) получаем:
![]() , (9)
, (9)
![]() , (10)
, (10)
где
 ,
,
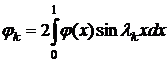 ,
,  .
.
Решая
задачу (9), (10), находим:
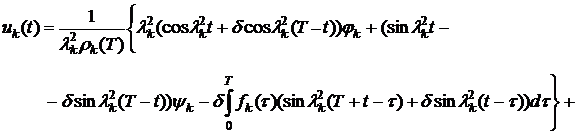
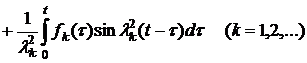 , (11)
, (11)
где
![]() .
.
Дифференцируя
(11) два раза, имеем:

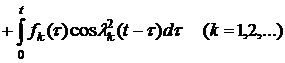 , (12)
, (12)
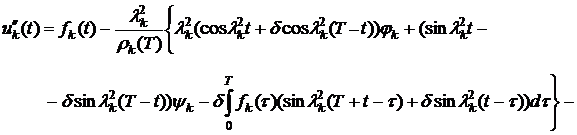
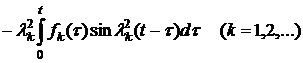 . (13)
. (13)
Нетрудно,
видеть, что
![]() .
.
Далее,
из (11), (12), (13) соответственно находим:
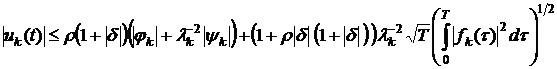 ,
,
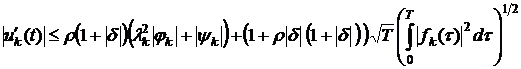 ,
,
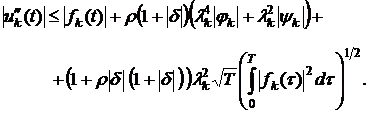
Отсюда
имеем:
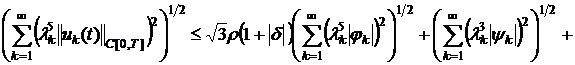
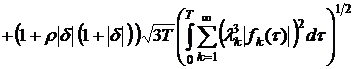 , (14)
, (14)
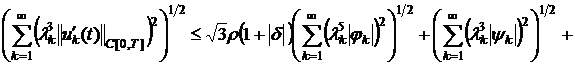
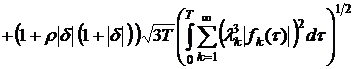 , (15)
, (15)
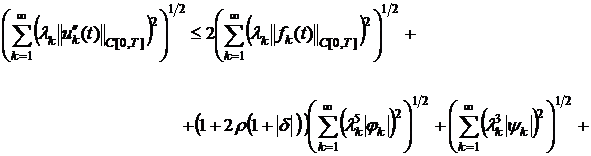
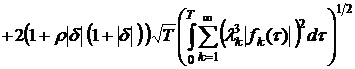 . (16)
. (16)
Справедлива
следующая
Теорема 2. Пусть ![]() и
и
1. ![]() ,
,
![]() ;
;
2. ![]() ,
,
![]() ;
;
3. ![]() ,
,
![]()
Тогда
функция
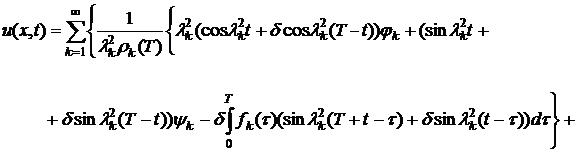
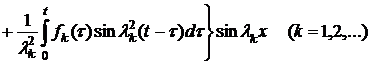 (17)
(17)
является классическим решением задачи
(1)-(3).
Доказательство. Принимая во внимание
условия теоремы 2, из (14), (15) и (16) соответственно получаем:
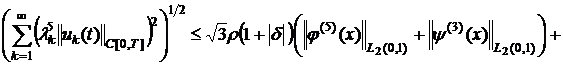
![]() , (18)
, (18)
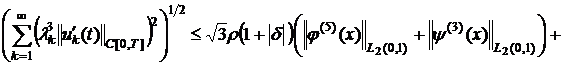
![]() , (19)
, (19)
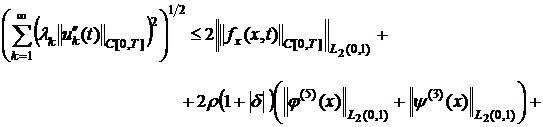
![]() . (20)
. (20)
Очевидно,
что
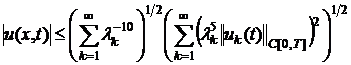 , (21)
, (21)
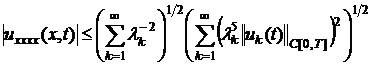 , (22)
, (22)
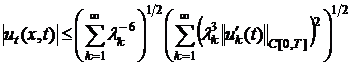 , (23)
, (23)
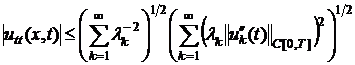 . (24)
. (24)
Из
(21)-(24), с учётом (18)-(20), следует, что функции ![]() ,
, ![]() и
и ![]() непрерывны в
непрерывны в ![]() . Непосредственной проверкой легко видеть, что функция
. Непосредственной проверкой легко видеть, что функция ![]() удовлетворяет
уравнению (1) и условиям (2),(3) в обычном смысле. Теорема доказана.
удовлетворяет
уравнению (1) и условиям (2),(3) в обычном смысле. Теорема доказана.
Литература
1.
А.Н.Тихонов,
А.А.Самарский. Уравнения математической физики. М.: Москва, 1972.
2.
В.И.Смирнов.
Курс высшей математики, т.V.
М.: Москва, 1957.
Поступила
в редакцию 22.07.2010 г.