Методы решения задачи гидроакустической совместимости гидролокационных станций в мультистатической системе подводного наблюдения

НА ГЛАВНУЮ

Михнюк Александр Николаевич,

аспирант Научного центра волновых исследований Учреждения Российской академии наук Института общей физики им. А. М. Прохорова РАН (филиал).

В данной работе рассматривается проблема гидроакустической совместимости однотипных гидролокационных станций (ГЛС), т.е. решается задача преодоления мешающего воздействия прямых полей от соседних станций на работу каждой станции в системе.

В настоящее время эта проблема не была эффективно решена ни в одной из существующих систем. Дело в том, что отношение амплитуды прямого поля соседней станции к амплитуде эхо-сигнала может достигать 10³ раз и более. При таких соотношениях никакой согласованный фильтр, и даже остронаправленная антенна не могут с достаточной эффективностью избавиться от мертвой зоны порожденной приходом прямого сигнала соседней станции. С этой проблемой борются либо разносом по частоте зондирующих сигналов (ЗС) разных станций, либо разносом по времени, т. е. увеличением периода повторения излучения. Первый путь приводит к сужению рабочего частотного диапазона каждой станции и как следствие понижению помехоустойчивости по отношению к реверберационной помехе. Например, для системы, состоящей из 10 станций, полоса каждой станции должна быть сокращена как минимум в 10 раз, что уменьшит помехоустойчивость к реверберационной помехе также в 10 раз. Второй путь – разнос излучения станций во времени. При этом увеличивается период обзора контролируемой области каждой из ГЛС, что отрицательно сказывается на эффективности последующего траекторного анализа обнаруженных целей вплоть до полной невозможности его проведения.

Столбовой путь решения этой проблемы – это применение адаптивных алгоритмов режекции прямого поля. Задача этих алгоритмов заключается в подавлении мощных прямых сигналов, приходящих от других ГЛС, до уровня, позволяющего распознать на их фоне слабые сигналы, отраженные от цели.

Оптимальный алгоритм режекции

Оптимальный алгоритм режекции прямых сигналов в мультистатической системе подразумевает исключение прямого поля из смеси сигналов, принимаемой каждой из станций. Построим такой алгоритм в предположении, что сигналы соседних ГЛС, а также их взаимно-корреляционные функции с эталонным сигналом нам известны априорно.

Рассмотрим гипотезу H₀ – эхо-сигнал от цели отсутствует. Измерение (выход согласованного фильтра (СФ) в одном из приемных каналов антенной решетки (АР) ГЛС) имеет вид:

. (1)

Здесь – комплексная взаимно-корреляционная функция (ВКФ) ЗС μ-ой станции с эталонным сигналом; – неизвестная комплексная амплитуда ЗС μ-ой станции; – распределенная по нормальному закону помеха со среднеквадратическим отклонением (СКО) ; – номера соседних станций, – номера временных отсчетов.

Плотность вероятности измерения (1):

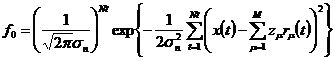. (2)

Ее логарифм:

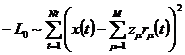. (3)

Введем обозначения:

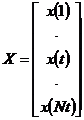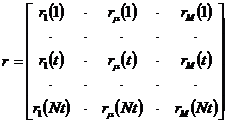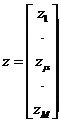, , . (4)

В этих обозначениях выражение для логарифма плотности вероятности (3) принимает вид:

. (5)

Минимизируем (5) по неизвестным комплексным амплитудам z:

Отсюда получаем оценку :

. (6)

Подставим оценку (6) в выражение для логарифма плотности вероятности (5):

. (7)

Здесь – проектор на подпространство мешающих сигналов, а – ортогональный ему проектор.

Рассмотрим гипотезу H₁ – эхо-сигнал от цели присутствует. В этом случае измерение принимает вид:

. (8)

Здесь – ВКФ эхо-сигнала с эталонным, которая нам также известна.

Плотность вероятности измерения (8):

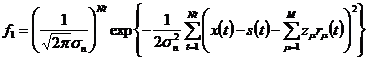. (9)

Ее логарифм:

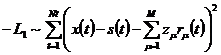. (10)

Введя обозначение

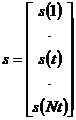(11)

и учитывая обозначения (4), введенные ранее, представим логарифм плотности вероятности измерения (11) в виде:

. (12)

Минимизировав выражение (12) по z, получим:

. (13)

Оптимальная решающая статистика:

. (14)

Далее представлены результаты, получаемые по описанному алгоритму при различном количестве мешающих станций (рис. 1 – 3).

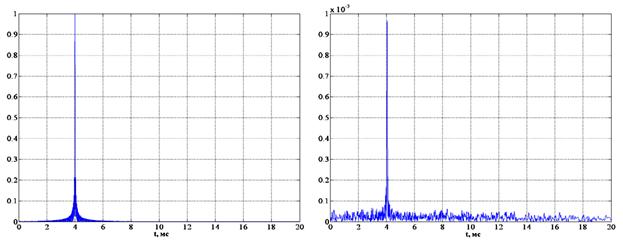
Рис. 1. Оптимальная режекция поля одного мешающего источника.

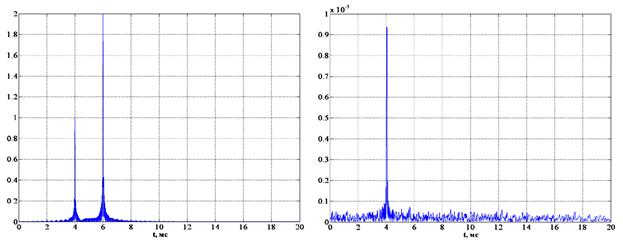
Рис. 2. Оптимальная режекция поля двух мешающих источников.

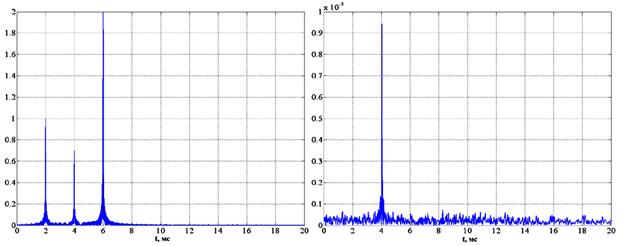
Рис. 3. Оптимальная режекция поля трех мешающих источников.

На этих рисунках приведены модули выхода СФ в одном из приемных каналов для случаев одного, двух и трех мешающих источников (слева) и модули его проекции на подпространство ортогональное подпространству мешающих сигналов. Амплитуда эхо-сигнала равна 10^-3, время его прихода – 4.05 мс. СКО распределенной помехи здесь также составляет 10^-3. Из приведенных результатов видно, что в результате применения описанной выше обработки мощные сигналы от соседних ГЛС режектированы полностью, а эхо-сигнал, который на левых графиках не виден, при этом передался практически без искажений.

Однако для того чтобы иметь возможность применения этого алгоритма, мы должны априори знать ВКФ зондирующих сигналов всех станций с эталонным. На самом деле мы этого не знаем, даже если измерим искажения, вносимые конкретным излучателем, так как при распространении возникают дополнительные искажения, вызываемые многолучевостью, а также частотной зависимостью затухания звука при распространении.

Режекция мощного прямого поля при неизвестных мешающих сигналах

Описание алгоритма

Отличием предлагаемого алгоритма от оптимального является то, что нам неизвестны сигналы, излучаемые соседними станциями. Здесь мы производим оценку этих сигналов на основании предположения, что их форма одинакова во всех приемных каналах принимающей станции. При этом режекция осуществляется на основании информации содержащейся только в сигналах принятых АР ГЛС на текущем импульсе.

Рассмотрим предлагаемый алгоритм подробнее.

Пусть на приемную антенну нашей ГЛС приходят прямые сигналы от M соседних станций, находящихся в ее поле видимости. Для простоты в качестве приемной антенны будем рассматривать цилиндрическую звукопрозрачную АР, состоящую из ненаправленных приемников. В этом случае выражение для принимаемой k-ым приемником АР смеси сигналов можно записать следующим образом:

. (15)

Здесь – сигнал, излучаемый μ-ой станцией, измеренный в центре принимающей станции; – задержки во времени прихода сигнала μ-ой станции на k-ый приемник, определяемые геометрией АР; – эхо-сигнал, отраженный от цели, измеренный в центре принимающей станции; – задержки во времени прихода эхо-сигнала на k-ый приемник, определяемые геометрией АР; , если цель присутствует в зоне обзора ГЛС и , если цель отсутствует; – шум на входе k-го приемника АР; t – время; – номера приемников в АР; – номера соседних ГЛС.

В частотной области выражение (15) будет иметь вид:

, (16)

где: – комплексный спектр сигнала, излучаемого μ-ой ГЛС; – комплексный спектр эхо-сигнала; – комплексный спектр шума на входе k-го приемника АР; – фазовый компенсатор для k-го приемника АР в μ-ом направлении; – круговая частота.

Так как режекция мешающих сигналов есть не что иное, как удаление этих сигналов из принятой смеси, то для возможности ее осуществления нам необходимо оценить форму этих мешающих сигналов.

Логарифм отношения правдоподобия измерения в частотной области в случае нормально распределенной помехи пропорционален следующей величине:

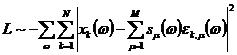Произведем оценку спектров сигналов соседних станций путем минимизации невязки пропорциональной минус логарифму отношения правдоподобия

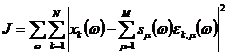(17)

по этим спектрам.

Преобразуем выражение для невязки J (17):

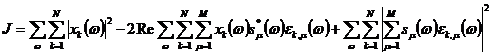
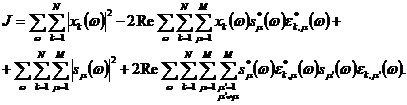(18)

Вычислим производные выражения (18) по величинам :

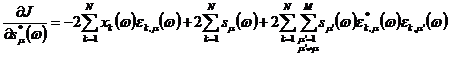. (19)

Приравняв производные (19) к нулю, получим для каждой частоты ω систему из M уравнений вида:

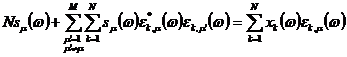. (20)

Введем следующие обозначения:

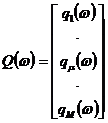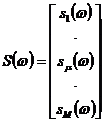, . (21)

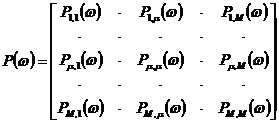
С учетом обозначений (21) система (20) примет вид:

. (22)

Решение этой системы:

. (23)

Подставив решение (23) в выражение для невязки (17) получим:

. (24)

Здесь .

Зная геометрию АР и направления на соседние ГЛС, мы можем вычислить задержки , т. е. сформировать матрицы и (21), и, следовательно, оценить спектр мешающих сигналов (23). Если же направления на соседние ГЛС априорно неизвестны или известны с недостаточной точностью, то их можно определить путем численной минимизации величины (24) по этим направлениям.

Сама режекция осуществляется вычитанием из спектра смеси, принятой k-ым приемником, спектров сигналов соседних станций, оцененных в соответствии с формулой (23):

. (25)

Величина представляет собой не что иное, как комплексный спектр сигнала принятого k-ым приемником в отсутствие прямого поля соседних станций. Применяя обратное преобразование Фурье [Марпл-мл. С.Л.] можно получить выражение для сигнала принятого k-ым приемником в отсутствие прямого поля соседних станций во временной области . Полученные таким образом сигналы или их спектры подвергаются далее типичной для ГЛС обработке, а именно согласованной фильтрации и формированию характеристик направленности.

Исследование эффективности алгоритма

Эффективность вышеописанного метода подавления прямого поля была исследована путем численного моделирования в среде Matlab.

Исследование было проведено для случая кольцевой звукопрозрачной АР с радиусом равным 15 см, состоящей из приемных элементов. В качестве ЗС использовался сигнал с линейной частотной модуляцией. Характеристики этого сигнала: полоса – 30 кГц, центральная частота – 75 кГц, длительность – 3 мс. Частота квантования АЦП – 300 кГц, что составляет 1.67 от удвоенной верхней частоты ЗС.

Для каждого приемного элемента такой АР задавалась входная смесь, состоящая из суммы эхо-сигнала и нескольких мешающих плюс белый шум с нулевым математическим ожиданием и СКО равным амплитуде полезного сигнала. Эхо-сигнал и мешающие сигналы задавались в виде плоских волн приходящих с различных направлений. Соотношение амплитуд мешающего и полезного сигналов задавалось исходя из условий, соответствующих реальным условиям функционирования ГЛС.

Построим отклик нашей АР на эту принимаемую смесь [Бьерне Л.; Ван Трис Г.; Кремер И.Я., Кремер А.И., Петров В.М.] (рис. 4).

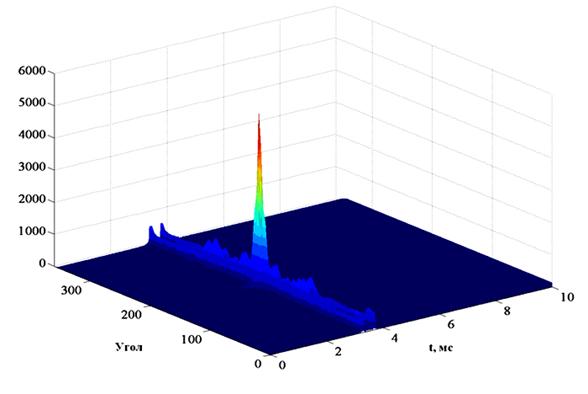
Рис. 4. Пространственный отклик АР на задаваемую входную смесь.

На рис. 4 на плоскости угол-задержка изображен пространственный отклик АР на 2 плоские волны с амплитудами 1 и 2·10^-3 приходящие с направлений 182º и 200º в моменты времени 3.5 и 3.6 мс соответственно. Как и ожидалось, здесь мы видим только один пик, соответствующий мощному мешающему сигналу, падающему с направления 182º, и его боковые лепестки. Уровень этого пика составляет A₀ = 5500 относительных единиц. Полезный эхо-сигнал на его фоне не виден.

Выполним далее обработку входной смеси в соответствии с предложенным алгоритмом. С помощью прямого преобразования Фурье [Сергиенко А. Б.] измерение во временной области преобразуем к измерению в частотной . Затем, зная геометрию АР нашей станции и направление на источник мешающего сигнала, вычислим задержки :

Здесь a – радиус АР, – направление на k-ый приемник АР. Подставляя вычисленные таким образом задержки в формулы (21) и (23) получим спектр мешающего сигнала .

Далее, подставив полученный спектр в формулу (25), осуществим режекцию, и после этого сформируем отклик АР на смесь, не содержащую мешающего сигнала (рис. 5).

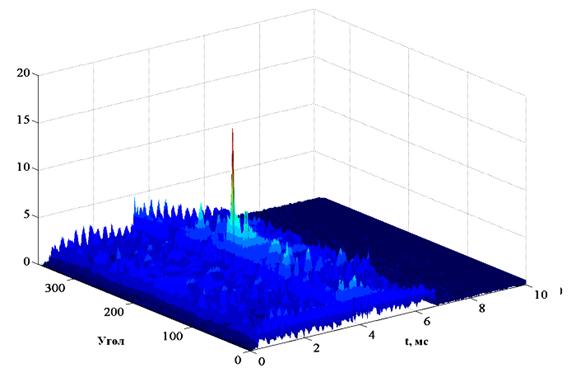
Рис. 5. Пространственный отклик АР на входную смесь после режекции.

На рис. 5 на плоскости угол-задержка приведен пространственный отклик АР станции на принятую смесь после режекции мешающего сигнала. На этом рисунке виден пик, который соответствует плоской волне приходящей с направления 200º, т.е. эхо-сигналу от цели, амплитуда которого в 500 раз меньше амплитуды мешающего сигнала. Уровень этого пика равен 16.5 относительным единицам. Помимо этого пика на рисунке видны остатки не полностью режектированного мешающего сигнала, уровень которых не превосходит 8 относительных единиц. Эти остатки обусловлены ошибками при оценке его формы. Сравнивая рис. 4 и 5, видим, что степень режекции мешающего сигнала можно оценить как 5500/8 ≈ 690 раз.

Этот результат получен в случае точно известного направления прихода мешающего сигнала. В реальных условиях это направление известно с некоторой ошибкой. Для того чтобы определить необходимую точность оценки направления прихода мешающего сигнала, построим зависимость степени режекции от ошибки при определении этого направления. Полученные результаты представлены в таблице 1.

Таблица 1.

№	Ошибка определения направления , º	Уровень остатка после режекции A, отн. ед.	Степень режекции A₀/A
1	0	8	690
2	0.001	8	690
3	0.002	10	550
4	0.005	22	250
5	0.01	45	120
6	0.02	90	60
7	0.05	220	25
8	0.1	450	12
9	1	4200	1.3

Как видно из приведенной таблицы уровень остатка, начиная с ошибки в 0.005º, становится пропорциональным ошибке. Равенство степени режекции при ошибках равных 0º и 0.001º обусловлено определяющим влиянием шума на оценку спектра и, соответственно, формы мешающего сигнала.

На основании полученных результатов можно сделать следующее заключение: для того, чтобы уровень эхо-сигнала был сравним с уровнем остатка мешающего сигнала после режекции или превосходил его, точность определения направления на мешающий источник должна быть выше 0.005º.

В реальных условиях направление на мешающий источник можно приблизительно определить по выходу ХН АР, которые мы можем сформировать с произвольным достаточно малым шагом. Однако, и в этом случае мы можем не получить достаточно точной оценки искомого направления. Это обуславливается влиянием шума и взаимным влиянием мешающих источников на положение максимумов, соответствующих направлениям на эти источники. Поэтому возникает необходимость оценивать направления на мешающие источники путем численной минимизации величины невязки (24) по этим направлениям.

Минимизацию можно провести следующим образом. За нулевое приближение принимаем оценки направлений на мешающие источники, полученные по выходу сформированных ХН. После этого производим режекцию вышеизложенным методом, с использованием этих направлений. Далее вычисляем величину невязки (24) и ее M-мерный градиент (координатами M-мерного пространства являются направления на мешающие ГЛС). За следующее приближение направлений на мешающие источники принимаем следующую величину [Максимов Ю.А.; Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М.]:

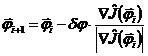
Здесь – шаг, величина которого определяется необходимой точностью определения направлений на мешающие источники. Таким образом, мы движемся в направлении обратном направлению градиента невязки , т.е. к ее минимуму. Итерации заканчиваются, когда выполняется условие . При этом за искомые направления принимаются направления, полученные на i-ой итерации.

Ниже приведем результаты, полученные в случае определения направлений на мешающие источники путем минимизации невязки (24) вышеописанным методом при различном количестве мешающих ГЛС. Во всех нижеприведенных результатах эхо-сигнал от цели представляет собой плоскую волну с амплитудой 0.002, приходящую с направления 200º в момент времени 3.6 мс, помеха представляет собой белый шум с СКО равным амплитуде эхо-сигнала.

В случае одного мешающего источника мешающий сигнал – плоская волна единичной амплитуды, падающая с направления 182º, момент ее прихода равен 3.5 мс. Нулевое приближение направления прихода мешающего сигнала в этом случае составило 181.985º. Оценка направления прихода мешающего сигнала после минимизации невязки (24) вышеописанным методом: 182º (рис. 6).

В случае двух мешающих источников мешающие сигналы – плоские волны с амплитудами 1.0 и 0.9, падающие с направлений 182º и 239º, моменты их прихода равны 3.5 и 3.8 мс соответственно. Нулевое приближение направлений прихода мешающих сигналов в этом случае составило 181.985º и 239.365º. Оценка направления прихода мешающего сигнала после минимизации невязки (24) вышеописанным методом: 181.9999º и 239.0003º (рис. 7).

В случае трех мешающих источников мешающие сигналы – плоские волны с амплитудами 0.7, 1.0 и 0.9, падающие с направлений 100º, 182º и 239º, моменты их прихода равны 5.0, 3.5 и 3.8 мс соответственно. Нулевое приближение направлений прихода мешающих сигналов в этом случае составило 100.365º, 181.985º и 239.365º. Оценка направления прихода мешающего сигнала после минимизации невязки (24) вышеописанным методом: 100.0005º, 182º и 238.9988º (рис. 8).

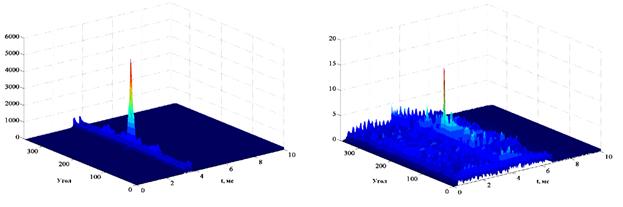
Рис. 6. Отклик АР на принимаемую смесь и результат режекции для случая одного мешающего сигнала.

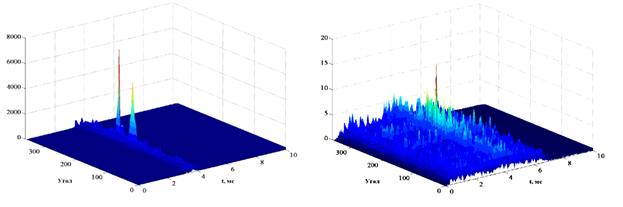
Рис. 7. Отклик АР на принимаемую смесь и результат режекции для случая двух мешающих сигналов.

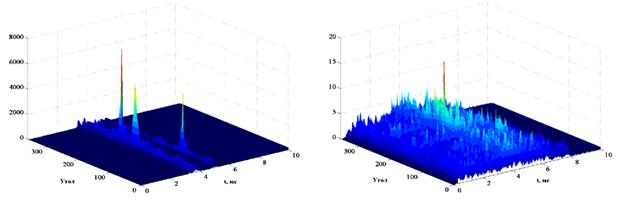
Рис. 8. Отклик АР на принимаемую смесь и результат режекции для случая трех мешающих сигналов.

На приведенных рисунках слева мы видим только пики, соответствующие мешающим сигналам, справа виден пик, который соответствует плоской волне приходящей с направления 200º, т.е. эхо-сигналу от цели, амплитуда которого в 500 раз меньше амплитуды мешающих сигналов.

В случае звуконепрозрачной АР, состоящей из приемников, которые имеют собственные ХН, можно также применять этот алгоритм, предварительно его модифицировав. Необходимость его модификации вызвана необходимостью определения амплитуды мешающих сигналов в каждом из приемных каналов. Алгоритм определения неизвестной амплитуды, при известной форме мешающих сигналов описан выше (оптимальный алгоритм режекции).

Выводы

· В отличие от оптимального алгоритма, вышеописанный алгоритм можно применять в случае априорно неизвестной формы мешающих сигналов.

· Применение вышеописанного алгоритма позволяет достигнуть достаточно высокой степени режекции (до 1000 раз).

· Для достижения существенной степени режекции необходимо очень точно определять направление прихода мешающего сигнала, что в свою очередь приводит к значительному увеличению вычислительных затрат.

· Основные вычислительные затраты в этом алгоритме приходятся на определение направлений прихода мешающих сигналов с необходимой точностью.

Литература

1. Бьерне Л. (ред.), Подводная акустика и обработка сигналов /пер. с англ., М.: Мир, 1985.

2. Ван Трис Г., Теория обнаружения, оценок и модуляции. т.3 Обработка сигналов в радио и гидролокации /пер. с англ., М.: Сов.радио, 1975.

3. Кремер И.Я., Кремер А.И., Петров В.М., Пространственно-временная обработка сигналов, М.: Радио и связь, 1984.

4. Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.

5. Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения: Пер. с англ. - М.: Мир, 1990.

6. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. – М.: Наука, 1978.

7. Сергиенко А. Б. Цифровая обработка сигналов. — 2-е. — Спб: Питер, 2006. — с. 751.

Поступила в редакцию 19.03.2010 г.