Разработка архитектуры публичного сервера для расчета распространения цунами в режиме онлайн

Булгаков Кирилл Владимирович,

магистр.

Новосибирский государственный университет

Научный руководитель – кандидат технических наук

Романенко А. А.

Целью данной работы является разработка архитектуры публичного сервера для расчета распространения волны цунами в режиме онлайн. В качестве целевой аппаратной платформы выбран процессор CELL B.E. [2]

Разрабатываемая система будет моделировать процесс распространения волны цунами. Это достаточно ресурсоемкая задача, а при учете того, что система должна достаточно быстро производить процесс моделирования и иметь возможность моделировать сразу несколько сценариев одновременно, становиться понятным, что мощности одного компьютера не хватит для решения поставленной задачи. Поэтому было принято решение о реализации системы в виде распределенной вычислительной системы архитектуры GRID [1]. Под сценарием в данном случае подразумеваются начальные данные, необходимые для моделирования, такие как начальное возмущение, скорости возмущения, временной шаг, количество итераций. Необходимость расчета различных сценариев на одно событие обусловлена тем, что точность моделирования определяется знанием начальных параметров смещения водной поверхности в эпицентре возмущения. Т.к. практически все узлы в системе однородны, т.е. нет существенных различий в производительности, аппаратная и программная платформы узлов не различаются, это существенно упрощает строение архитектуры. Архитектуру системы можно представить следующим образом (Рис. 1). Вычислительная среда представлена на рис. 2.

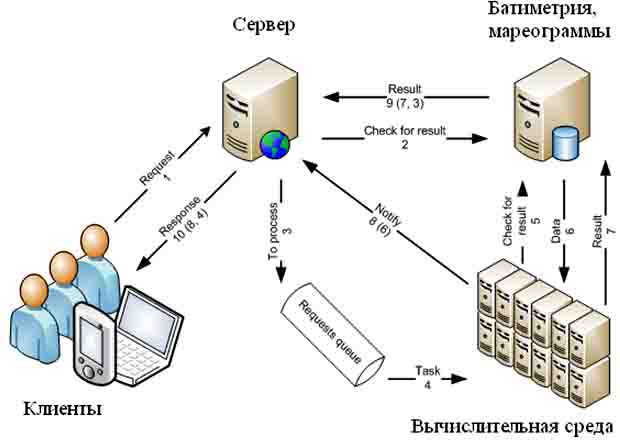
Рис. 1.

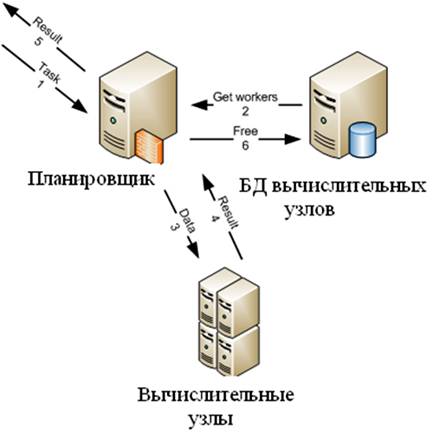
Рис. 2.

Клиент загружает на сервер сценарий, который он хочет смоделировать. Сервер проверяет в базе данных, моделировался ли такой же сценарий до этого момента. Если такой сценарий уже моделировался, то из базы данных загружает решение и отсылается клиенту. Если моделировался подобный сценарий, т.е. начальное возмущение, скорости и временной шаг совпадают, а количество итераций отличается, то решение подобного сценария загружается из базы данных и используется для получения более быстрого решения текущего сценария. Решение сценария производится следующим образом. Весь сценарий разбивается планировщиком на подзадачи, которые рассылаются на вычислительные узлы. Вычислительный узел решает свою подзадачу и возвращает ответ планировщику, который воспроизводит решение сценария из решений подзадач. Т.к. вычислительные узлы практически однородны, за исключением скорости их сетевого соединения, а вычислительные трудоемкости подзадач одного сценария не различаются, то в процессе моделирования можно собрать статистику, показывающую, за какое в среднем время конкретный вычислительный узел решает одну подзадачу. Эта информация хранится в базе данных вычислительных узлов. На основе этой статистики вычислительные узлы можно условно отнести к быстрым, средним или медленным. Так же следует сказать о следующей функциональности, присутствующей в системе. Рассмотрим ситуацию, когда планировщик разбил весь сценарий на девять подзадач. Восемь подзадач попали на быстрые вычислительные клиенты, а одну подзадачу решает медленный клиент. Вследствие такого распределения естественно возникнет ситуация, когда быстрые клиенты посчитали свои задачи, вернули результат планировщику и получили для расчета следующую подзадачу. Медленный клиент все еще будет находиться в процессе расчета своей задачи. В этом случае планировщик может прервать решение подзадачи на одном из быстрых клиентов, и выслать ему задачу, которую решает медленный клиент. Быстрый клиент решит подзадачу и вернет решение планировщику, т.е. расчет сценария завершится.

Вся система является динамической структурой, новые вычислительные узлы могут подключаться к системе во время работы, а уже подключившиеся – выходить из системы. Для процесса моделирования используется модель, описывающая распространение длинных волн в бассейне с произвольным рельефом дна, основанная на нелинейных уравнениях мелкой воды

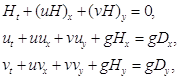                                                                                    (1)

где H(x, y, t) = n(x, y, t) + D(x, y, t); n - высота волны, отмеряемая от невозмущенного уровня, D - функция, описывающая рельеф дна, u(x, y, t), v(x, y, t) – скорости вдоль x и y соответственно, g – ускорение свободного падения. Систему (1) можно записать в следующем виде

                                                                                          (2)

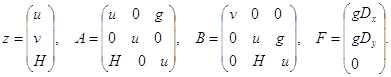
Алгоритм численного решения системы уравнений (2) строится на основе метода расщепления [3]. Для этого рассмотрим две вспомогательные системы, каждая из которых зависит только от одной пространственной переменной:

                                                                                   (3)

                                                                                    (4)

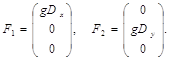
Обе системы могут быть преобразованы в каноническую форму

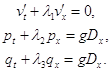                                                                                                      (5),

где

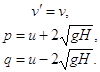
 инварианты системы (2) и

Численный алгоритм для решения системы (1) описывается следующим образом: после загрузки начальных данных и инициализации переменных, переменные расчетной сетки рассчитываются при помощи конечной разностной схемы. Каждый раз, одни этап алгоритма разделяется на два подэтапа. Каждый подэтап состоит из расчета инвариантов v', p, q использующих исходные значения переменных и последовательного решения канонической системы по направления координатных осей X и Y. После завершения текущего такта значения исходных переменных u, v, H должны быть восстановлены, используя новые значения инвариантов. Метод характеристической линии использовался, чтобы постановки граничные условия для системы. На границах открытого моря используются следующие условия:

, где  (т.е. r = p или q). На границе сухопутной области используются условия идеального отражения v = 0, p = -q. Для численного решения системы используется следующая разностная схема

где ,,.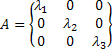

Можно заметить, что вычисления вдоль координат могут быть выполнены независимо друг от друга. Это используется для увеличения производительности путем распараллеливания.

Программирование процессора CELL B.E. существенно отличается от программирования классических процессоров архитектуры x86. При программировании CELL B.E. нужно писать сразу две программы – одну для PPE процессора, а другую для SPE процессоров. PPE процессор в программе играет роль менеджера ресурсов, а SPE процессоры – вычислительные блоки. Причем SPE процессоры имеют достаточно маленький объем памяти и не могут напрямую работать с памятью PPE. Поэтому программисту приходится вручную работать с контроллером шины, для того, чтобы загружать нужные фрагменты данных из памяти PPE в память SPE.

На данный момент реализована рабочая версия вышеприведенной математической модели для процессора CELL B.E. На этапе тестирования находится архитектура системы разбиения сценария на части и раздачи частей разным вычислительным узлам, которая будет использоваться в публичном сервере.

Литература

1.                  M. L. Bote-Lorenzo, Y. A. Dimitriadis, E. Gomez-Sanchez, Grid Characteristics and Uses: a Grid Definition, LNCS 2970, pp. 291 – 298.

2.                  J. A. Kahle, M. N. Day, H. P. Hotstee, C. R. Johns, T. R. Maeurer, D. Shippy, Introduction to the Cell multiprocessor, IBM Journal of Research and Development, pg. 589.

3.                  В. В. Титов, Метод численного расчета цунами с учетом трансформации волны на мелководье, Препринт, Новосибирск 1988.

Поступила в редакцию 28.04.2011 г.