Применение графо-аналитических моделей при верификации программных продуктов
Андронов Алексей Викторович,
аспирант Санкт-Петербургского национального научно-исследовательского университета информационных технологий, механики и оптики.
Верификации программных продуктов является актуальной проблемой информационной безопасности. Актуальность проблемы определяется отсутствием автоматизированных средств гарантированного выявления недекларированных (далее – НДВ) возможностей. На данный момент, не один из способов верификации не дает 100% вероятность отсутствия НДВ в проверяемом программном продукте. Методика верификации, освещенная в данной статье, - попытка решения данной проблемы.
Научно-технические аспекты процедуры сертификации по требованиям безопасности информации программных продуктов ФСТЭК России предусматривают наличие обоснованных гарантий по отсутствию НДВ. В тоже время, имеющиеся средства выявления НДВ и антивирусной защиты не дают высоких гарантий по их отсутствию, что заставляет проводить исследования по методам их гарантированного формализованного выявления и диагностики.
В данной статья описывается новая методика верификации программных средств с использованием графо-аналитической модели и комплексных кубических покрытий.
Любая программа реализует тот или иной вычислительный процесс, который порождается путём интерпретации её команд процессором – реальным или виртуальным. Переход от программ к вычислительным процессам позволяет осуществить поиск решений верификации программ в общем виде.
Описанием вычислительного процесса может служить его графо-аналитическая модель (ГАМ) и её описание в виде комплексных кубических покрытий [1].
ГАМ можно построить либо путём дешифрации машинного кода программы на основе системы команд процессора с использованием метода структурирования [2], либо построением её по техническому заданию (спецификации программы). Формализация построения ГАМ программы и её комплексного покрытия базируется на концептуальной двухконтурной итерационно-рекурсивной модели вычислительного процесса, порождаемого процессором при интерпретации команд программы. ГАМ представляется в виде множества вершин и связей (дуг) между вершинами. Вершины могут быть двух типов: линейными, в которых осуществляются вычисления по итеративным и рекуррентным формулам, и условными, в которых вычисляются значения условий-предикатов (УП). Связи являются направленными и осуществляют переход от вершины к вершине с помощью булевых функций управления. Комплексное покрытие объединяет в себе функции управления, логические переменные условий-предикатов и алгебраические выражения вычисляемых переменных. Покрытия строятся по ГАМ методом перебора путей на графе в виде последовательности линейных и условных вершин и связей между ними.
Таким образом, предложенная двухконтурная итерационно-рекурсивная модель вычислительного процесса программ, ГАМ на её основе и построение комплексных кубических покрытий, объединяющих в себе булевы функции, переменные и алгебраические выражения, позволяют перейти от анализа программ к анализу вычислительных процессов. Это дает возможность построить автоматизированные системы для решения задач верификации и тестирования программ, поиска недекларированных возможностей, средств защиты и анализа вирусной опасности.
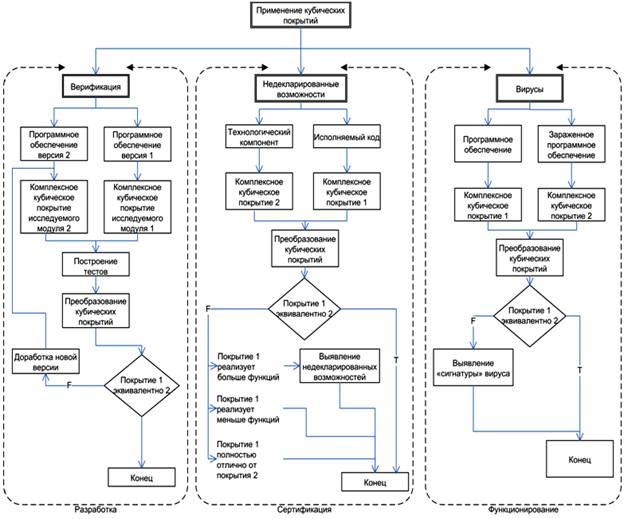
Применение комплексных кубических покрытий. Область применения предлагаемой методики верификации можно разделить на три направления (рис. 1).
Рис. 1. Применение кубических покрытий.
Верификация. Под верификацией понимается установление соответствия между различными программами. Необходимость в этом действии может возникнуть по следующим причинам:
1) Иногда программный продукт может разрабатываться различными группами проектантов. В этом случае можно верифицировать различные варианты реализаций между собой для повышения объективности и качества выбора конкретной версии.
2) В ходе жизненного цикла программа может подвергаться различным модификациям: обновление версии или устранение ошибки. Верификация в данном случае позволяет зафиксировать наличие и/или устранение ошибки, подтвердить идентичность логики программ, установить измененные элементы логики.
Выявление недекларированных возможностей и мертвого кода. В данном направлении ведется сравнение кубического покрытия построенного по исполняемому коду программы с кубическим покрытием, построенным на основе ее полной спецификации.
Определим вычислительный процесс как процесс преобразования информации по формулам и алгоритмам, осуществляющих вычисление значений некоторого множества переменных. Вычисление значений переменных по разным формулам и алгоритмам происходит под управлением заданного множества неравенств-отношений, которые задают условия-предикаты, так как каждое отношение может либо выполняться, либо не выполняться, т.е. принимать два значения: true и false и, следовательно, образуют предикат на множестве значений переменных, входящих в левую и правую части неравенств. Для описания вычислительного процесса, порождаемого программой, необходимо построить модель, которая позволит формализовать его описание и упростить решение различных задач синтеза и анализа с применением аппарата теории множеств и алгебры логики. В качестве такой модели удобно использовать графо-аналитическое представление вычислительного процесса [7]. В вершинах графа располагаются итеративные и рекуррентные формулы и условия-предикаты (отношения). Связи между вершинами задаются дугами. В общем случае, в вершине может размещаться любой алгоритм преобразования информации. Дуги управления образуют конъюнкции условий-предикатов и их дизъюнкции образуют булевы функции. Основной задачей исследования вычислительного процесса является его верификация в соответствии с декларацией и состоит в верификации декларированных и недекларированных его возможностей и в поиске несуществующих значений, образующих множество don`t care.
Таким образом,
задача верификации вычислительного процесса может быть сведена к поиску НДВ и
конъюнкций условий-предикатов, тождественно равных нулю, для которых системы
неравенств не имеют решений. НДВ на графе вычислительного процесса образуют
множество вершин и дуг, недостижимых через входные последовательности наборов,
построенных по декларации и don`t care, которые порождают частично-определенные
булевы функции. Эти функции при их отображении на n-мерный двоичный куб ![]() могут быть заданы покрытиями комплекса
могут быть заданы покрытиями комплекса ![]() , где f=1 (декларированные возможности,
определенные спецификацией),
, где f=1 (декларированные возможности,
определенные спецификацией), ![]() , где f=0 (НДВ) и
, где f=0 (НДВ) и ![]() , где f=d (don`t care). В случае
если верифицируемая программа в точности реализует логику, заданную
спецификацией, покрытие
, где f=d (don`t care). В случае
если верифицируемая программа в точности реализует логику, заданную
спецификацией, покрытие ![]() будет
эквивалентно покрытию, построенному по спецификации, а покрытия
будет
эквивалентно покрытию, построенному по спецификации, а покрытия ![]() и
и ![]() равны пустому множеству. При отображение
функций, заданных спецификацией, на n-мерный двоичный куб
равны пустому множеству. При отображение
функций, заданных спецификацией, на n-мерный двоичный куб ![]() , они могут быть заданы покрытием
, они могут быть заданы покрытием
![]() . Таким образом, мы
получаем равенство, позволяющее нам верифицировать логику проверяемой
программы:
. Таким образом, мы
получаем равенство, позволяющее нам верифицировать логику проверяемой
программы:
![]()
Если правая
часть равенства эквивалентна пустому множеству, то можно делать вывод о том,
что логика проверяемой программы в точности соответствует логике заложенной в
спецификации. В противном случае проводится дальнейший анализ покрытий ![]() и
и ![]() .
.
Исследование вирусов. Как и при поиске недекларированных возможностей исследуемым объектом является логика работы программ. Предполагается использовать разницу кубических покрытий зараженного экземпляра программы и «чистого». Найденная разница отображает логику вируса. В дополнении с данными о командах обработки данных назовем ее сигнатурой вируса.
Используя подобные сигнатуры можно исследовать программы на наличие вирусов и логику работы вируса.
Данное направление требует отдельных исследований и дополнительных экспериментальных данных.
В настоящее время основной уязвимостью в программном обеспечении является наличие недекларированных возможностей. Ни одно из существующих инструментальных средств поиска недекларированных возможностей не дает гарантий их обнаружения. Применение комплексных кубических покрытий позволит гарантированно решить данную задачу. Кроме этого существуют перспективы использования кубических покрытий в других областях безопасности информации.
Литература
1. Немолочнов О.Ф., Зыков А.Г., Поляков В.И., Осовецкий Л.Г., Сидоров А.В., Кулагин В.С. Итерационно-рекурсивная модель вычислительных процессов программ / «Известия вузов. Приборостроение» / Том 48, №12, СПб, декабрь 2005, с.14-20.
2. Немолочнов О.Ф., Зыков А.Г., Поляков В.И. Кубические покрытия логических условий вычислительных процессов и программ. / Научно-технический вестник СПбГУ ИТМО. Выпуск 14. Информационные технологии, вычислительные и управляющие системы / Гл. ред. В.Н. Васильев.- СПб: СПбГУ ИТМО, 2004. с.225-233. [1]
3. Зыков А.Г., Немолочнов О.Ф. Поляков В.И., Сидоров А.В. Структурирование программ и вычислительных процессов на множество линейных и условных вершин / Научно-технический вестник СПбГУ ИТМО. Выпуск 19. Программирование, управление и информационные технологии / Гл. ред. В.Н. Васильев.- СПб: СПбГУ ИТМО, 2005. с.207-212. [2]
4. Грис Д. Наука программирования. – М.: Мир, 1984.
5. Компаниец Р.И. Инструментальные средства анализа и защиты программного кода от использования недокументироаннных возможностей / Конференция «Защита информации в современных условиях – основа сохранения и развития бизнеса», 2006.
6. Лаздин А.В., Немолочнов О.Ф. Метод построения графа функциональной программы для решения задач верификации и тестирования / Научно-технический вестник СПб ГИТМО (ТУ). Выпуск 6. Информационные, вычислительные и управляющие системы / Гл. ред. В.Н. Васильев. – СПб.: СПб ГИТМО (ТУ), 2002.
7. Немолочнов О.Ф., Зыков А.Г., Поляков В.И. Комплексные кубические покрытия и графо-аналитические модели как средство описания вычислительных процессов программ. /Труды Международной научно-техническох конференций «Интеллектуальные системы» (AIS’06) и «Интеллектуальные САПР» (CAD-2006), Научное издание в 3-х томах- М.: Физматлит, 2006, Т2.- 588с. - ISBN 5-9221-0686-4.
Поступила в редакцию 27.10.2011 г.