Решение нормального эллиптического интеграла Лежандра 2-го рода

.

Мазенков Игорь Иванович,

ведущий инженер-конструктор ЗАО «Коминвест-АКМТ».

В интегральном исчислении, эллиптический интеграл появился в связи с задачей вычисления длины дуги эллипса и был впервые исследован Джулио Фаньяно и Леонардом Эйлером.

В общем случае, эллиптический интеграл не может быть выражен в элементарных функциях; исключением являются случаи, когда P имеет повторяющиеся корни или когда R(x,y) не содержит нечетных степеней y.

Для нахождения решения эллиптического интеграла я рассмотрел эллипс как трехмерную функцию, все точки которой лежат в одной плоскости под углом α к плоскости круга (частного случая эллипса, где k=1). В результате получил следующее решение эллиптического интеграла 2-го рода:

(1)

Где: 0<Θ<90 (т.е. в пределах ¼ эллипса), 0≤k≤1 (коэффициент сжатия эллипса).

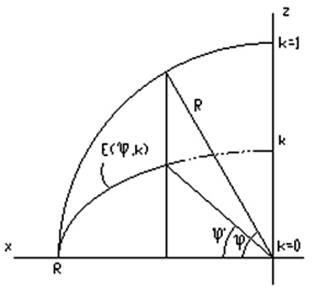
Рис. 1.

Доказательство

Для решения эллиптического интеграла рассмотрим эллипс как трехмерную функцию, все точки которой лежат в одной плоскости.

В плоскости XZ строим эллипс с коэффициентом сжатия k (0≤k≤1) так, как показано на рис. 2.

Через большую ось эллипса проводим плоскость под таким углом α, чтобы получить окружность радиусом R:

                                                                                                     (2).

Далее, если условно катить эллипс по плоскости XY вдоль оси Х, то получим развертку эллипса где , одновременно на плоскости XY будет образовываться развертка окружности, где:

;

                                                                                       (4)

 - угол касательной в т. М                                               (5)

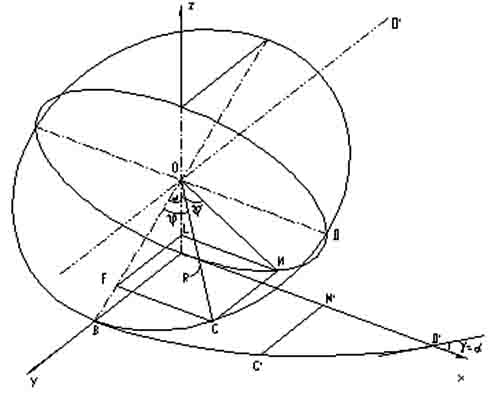
Рис. 2.

При повороте эллипса на 90⁰ вдоль ось Х развертка эллипса и кривая окружности в плоскости XY сойдутся в т.D’ так, что образуют касательную под углом

При различных k (0≤k≤1) в плоскости ХY образуется семейство кривых от окружностей. При k=1 эллипс является кругом и длина ¼ развертки на оси Х равна длине ¼ длины окружности:

 .

При k=0 у эллипса один из радиусов стремится к нулю и α=90⁰ . При этом кривая окружности на плоскости полностью совпадает с самой окружностью (радиусом R). Соответственно, длина эллипса при угле φ равна l=Rcosφ.

Особый интерес представляют кривые при 0<k<1.

Рассмотрим отдельно эти кривые на плоскости ХY (рис. 3).

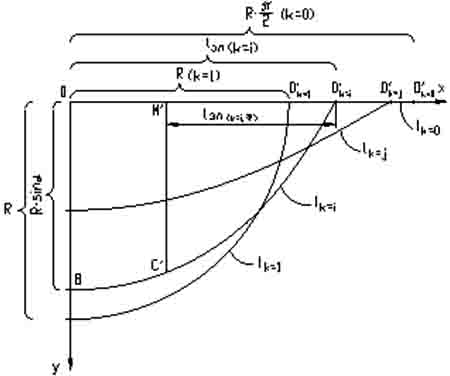
Рис. 3.

Длина всех этих кривых одинаковая (для искомого угла ϕ 0≤ϕ≤90). С’M’- известно. BC’- известно.

Осталось определить .

Для этого все кривые сместим влево так, чтобы точки D совпали с началом координат О (рис. 4).

При уменьшении коэффициента сжатия эллипса k кривая окружности на плоскости XY распрямляется. При этом хорда r_ϕ начинает увеличиваться на величину  и получаем:

                                                                                                         (6)

Дальше, по теореме Пифагора определяем искомую длину дуги эллипса l_эл при угле ϕ:

                                                                                              (7)

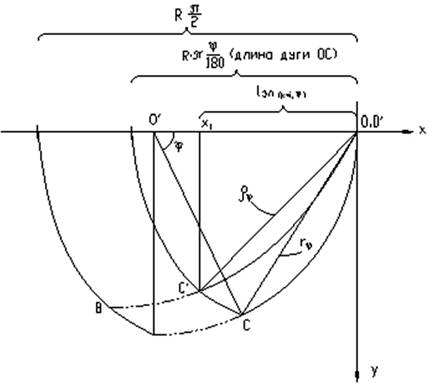
Рис. 4.

Подставив все найденные параметры в ф-лу (7), окончательно получим:

или

Литература

1.                  Камке Э. Справочник по обыкновенным дифференциальным уравнениям, М., Наука, 1976.

2.                  Пискунов Н.С. Дифференциальные и интегральные исчисления. В 2-х томах. Том 2. Интегралл-Пресс. 2009.

3.                  Зарубин В.С. Интегральные исчисления функций одного переменного. Том 6. МГТУ им. Баумана. 2006.

Поступила в редакцию 14.12.2011 г.