Центробежные силы инерции
Берников Василий Русланович,
инженер.
Рассмотрим трубчатое кольцо (Рис. 1) со средним радиусом R, заполненное жидкостью, двигающейся равномерно с угловой скоростью ω относительно центра О. Центробежная сила [1], действующая на точечный элемент жидкости массой ∆m будет равна Fц = ∆m ω2 R. В любом сечении кольца для одинаковых элементов центробежная сила будет по величине одинакова и направлена по радиусу от центра, растягивая кольцо.
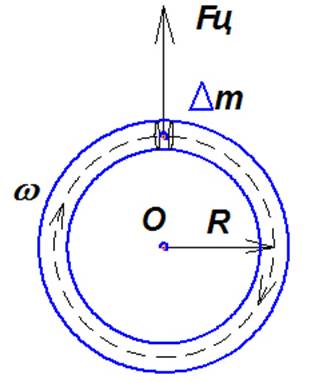
Рис. 1.
Теперь разделим пополам кольцо (Рис. 2) и соединим торцы такой же трубкой по дуге со средним радиусом R1. Пусть радиус R1 << R.
срочная доставка грузов здесь delby.ru
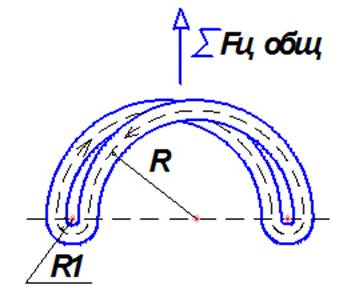
Рис. 2.
Равнодействующая центробежных сил, действующая на два элемента ∆m в верхней полуплоскости (граница верхней и нижней полуплоскости показана штриховой линией) обоих полуколец будет равна
Fц общ = 2∆m ω2 R.
Равнодействующая центробежных сил, действующая на два элемента ∆m в нижней полуплоскости обеих дуг будет равна
Fц1 общ = 2∆m Ω2 R1.
Так как R1 << R, то центробежной силой Fц1 общ можно пренебречь. Очевидно, что суммарная ∑ Fц общ центробежная сила, действующая в верхней полуплоскости на все элементы ∆m, будет действовать в направлении как показано на рисунке 2, так как полукольца симметричны относительно средней линии. Известно, что центробежная сила – это сила инерции, которая является внешней [2] для замкнутой системы. По второму закону Ньютона производная общего импульса системы тел равна сумме внешних сил [1], действующих на систему, то есть можно записать dK/dt = ∑ Fц общ.
Таким образом показана возможность суммирования центробежной силы в определённом направлении.
Литература
1. Курс теоретической механики: учебник / А.А. Яблонский, В.М. Никифорова. – 15-е изд., стер. – М.: КНОРУС, 2010.
2. Хайкин С.Э., Физические основы механики, М.: Наука, 1971.
Поступила в редакцию 26.04.2011 г.