Применение преобразования Вигнера для анализа сигналов малозаметных РЛС
Коротков Андрей Владимирович,
соискатель Санкт-Петербургского государственного университета «ЛЭТИ»,
Рассматривается задача частотно-временного анализа сигналов малозаметных РЛС с помощью преобразования Вигнера. Показано применение данного метода, приведены результаты экспериментов.
Ключевые слова: частотно-временной анализ, преобразование Вигнера, радиолокационные сигналы.
Введение
В настоящее время большое внимание уделяется сигналам малозаметных РЛС с низкой вероятностью обнаружения, которая достигается специальными мерами снижения мощности передатчика и уровня боковых лепестков, а так же существенным увеличением полосы пропускания. При этом уровень сигнала зачастую не превышает уровень шума.
По мнению зарубежных экспертов, использование данных МРЛС является одним из ключевых подходов к решению задач обнаружения и распознавания малоразмерных воздушных, а также наземных целей, замаскированных или находящихся в естественных укрытиях.
Часто для анализа и обработки соответствующих сигналов применение традиционных методов, основанных только на различных модификациях преобразования Фурье, оказывается малоэффективным. Большое значение имеет разработка новых методов анализа сигналов МРЛС.
Основными причинами, усложняющими решения этой проблемы, являются: низкое отношение сигнал/шум на входе приемника, многообразие видов модуляции и априорная неопределенность параметров принимаемых излучений. В этом случае качественные показатели обнаружения и измерения параметров зависят не от энергии сигнала, а от его пиковой мощности.
До настоящего времени средства радиотехнического мониторинга успешно справлялись с решением указанных задач. Это объясняется тем, что принимаемые от традиционных радиолокационных станций сигналы имеют достаточно большую пиковую мощность. В отличие от них сигналы МРЛС работают почти в непрерывном режиме и отличаются большой длительностью и малой средней мощностью излучения.
Качественные показатели обнаружения сложных сигналов МРЛС можно повысить за счет применения новых частотно-временных преобразований.
В настоящее время, чаще всего, для частотно-временного анализа излучений современных РЛС, применяется технология цифрового обнаружения, в основе которого лежит реализация преобразования Фурье (ДПФ) [1].
Существенным недостатком данного метода является невозможность получения одновременно высокого разрешения по времени и частоте.
Поэтому, для сложных колебаний с широким спектром и низким соотношением сигнал/шум, применение только данного преобразования не позволит получить набор признаков обеспечивающих требуемую контрастность образов, необходимую для реализации процедур достоверного распознавания.
Для разрешения этого противоречия в современной математике разработан ряд методов анализа нестационарных сигналов (к этому классу сигналов относятся и квази-непрерывные излучения МРЛС).
В данной работе предлагается применение преобразования Вигнера (ПВ) для анализа сигналов МРЛС.
1. Преобразование Вигнера
Преобразование Вигнера [2], введенное в 1932 г. Е. Вигнером в задачах квантовой термодинамики и в 1948 г. использованное Дж. Виллем при обработке сигналов, имеет вид:
![]()
Оно представляет собой преобразование Фурье от произведения ![]() , где f(t)
– анализируемый сигнал, а символ «*» обозначает операцию комплексного сопряжения.
, где f(t)
– анализируемый сигнал, а символ «*» обозначает операцию комплексного сопряжения.
Для дискретного сигнала ![]() , ПВ с прямоугольным окном длины 2N
представим так:
, ПВ с прямоугольным окном длины 2N
представим так:
![]() (1)
(1)
где ![]() ,
,
![]() ,
, ![]()
Используя подстановку![]() и учитывая, что
и учитывая, что ![]() , формулу (1) можно представить
в виде
, формулу (1) можно представить
в виде
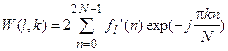 , где
, где
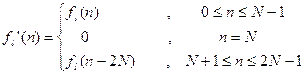
2. Применение ПВ для анализа сигналов МРЛС
Основными видами внутриимпульсной модуляции, применяемые в МРЛС, являются: частотная модуляция (ЧМ), частотная и фазовая манипуляция и их комбинации. Наиболее распространенной является ЧМ с линейно изменяющейся частотой (ЛЧМ). Для кодирования фазы зондирующего сигнала широко используются коды Баркера, полифазные коды Франка, Р1, Р2, Р3 и Р4 [3].
2.1 ПВ сигналов, содержащих коды Баркера
Кодовые последовательности Баркера представляют собой двоичную фазовую манипуляцию. Фаза сигнала может принимать два значения 0 и 180 градусов.
В качестве примера рассмотрен сигнал со следующими параметрами: частота несущей fн= 2.1 ГГц, полоса сигнала 250 МГц, код Баркера длинны 11, частота дискретизации Fd =10 ГГц.
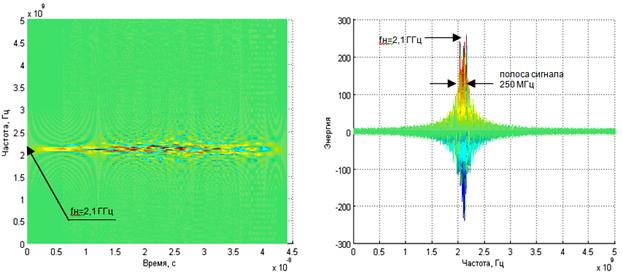
Рис. 1. Преобразование Вигнера для кода Баркера длинны 11.
На рис. 1 видно, что ПВ позволяет точно определить полосу рассматриваемого сигнала и несущую частоту. При этом определение вида кодовой последовательности затруднено.
2.2 ПВ сигналов, содержащих полифазные коды
Формулы, описывающие закон изменения фазы и частоты кодов имеют вид [3]:
Код Франка ![]()
Код Р1 ![]()
Код Р2 ![]()
Код Р3 ![]()
Код Р4 ![]()
где ![]() –номер
отсчета на заданной частоте,
–номер
отсчета на заданной частоте, ![]() – номер частоты,
– номер частоты, ![]() -фаза
-фаза ![]() – го отсчета
– го отсчета ![]() - ой частоты,
- ой частоты, ![]() – длина кода (для
кода Р3 и Р4 длина кода равна N).
– длина кода (для
кода Р3 и Р4 длина кода равна N).
В качестве примера рассмотрен сигнал со следующими параметрами: полоса сигнала 1 ГГц, код Франка N=4, частота дискретизации Fd =10 ГГц.
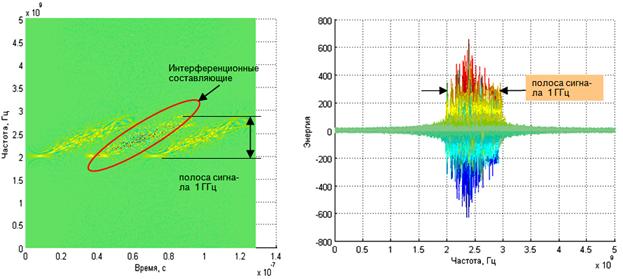
Рис. 2. Преобразование Вигнера для кода Франка.
ПВ кода Франка позволяет определить основные параметры исследуемого сигнала (рис. 2). Но при этом, на временной диаграмме наблюдается появление интерференционных составляющих, затрудняющих анализ.
2.3. ПВ ЛЧМ сигнала
В качестве примера рассмотрен следующий сигнал: девиация частоты 1 ГГц, частота дискретизации Fd =10 ГГц. Результаты представлены на рис.3.
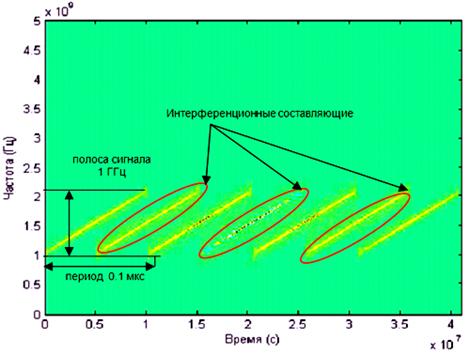
Рис. 3. Преобразование Вигнера для кода Франка.
Рассмотренный модельный сигнал представляет собой четыре ЛЧМ участка с периодом 0.1 мкс. Достаточно точно определены основные параметры ЛЧМ сигнала: девиация частоты, период модуляции. При этом (аналогично ПВ кода Франка), наблюдается появление интерференционных составляющих, затрудняющих дальнейшую обработку.
Заключение
ПВ любого многочастотного сигнала характеризуется появлением интерференционных составляющих, амплитуда которых сравнима с амплитудой реального сигнала, а частота равна половине суммы двух несущих реального сигнала. Причем они имеют место, как на спектрограмме, так и на временной диаграмме. Вследствие этого необходимо применение специальных алгоритмов фильтрации данных составляющих.
Тем не менее, временная диаграмма дает возможность оценить закон перестройки частоты и фазы сигнала, а так же измерить его основные параметры.
Таким образом, применение данного преобразования является перспективным и может применяться для уточнения данных, полученных с помощью ДПФ.
Литература
1. Айфичер Эммануил С., Джервис Барри У. Цифровая обработка сигналов: пер. с англ. – М.: Издательский дом «Вильямс», 2004. – 992 с.
2. Mecklenbrauker W., Hlawatsch, F. The Wigner Distribution: Theory and Applications in Signal Processing, Elsevier, Amsterdam, 1997.
3. Pace Phillip E. Detecting and Classifying Low Probability of Intercept Radar 2009. Artech House, 685 Canton Street Norwood.
Поступила в редакцию 21.04.2011 г.