Статистические испытания алгоритмов приема и демодуляции сигналов в цифровых радиоканалах
Иванов Максим Сергеевич,
адъюнкт,
Табырца Дмитрий Владимирович,
адъюнкт,
Малисов Николай Павлович,
адъюнкт.
Военный авиационный инженерный университет, г. Воронеж.
Научный руководитель – доктор технических наук, профессор
Бураченко Дмитрий Леонидович.
В статье приводятся результаты статистического испытания приёмника (демодулятора), обеспечивающего эффективную компенсацию помехи при приёме цифровых сигналов с низкой энергетикой в условиях помехи.
Анализ показывает, что в радиоканалах передачи данных с частотной полосой до 5 МГц возможен теоретически и реализуем практически приём и обработка цифровых сигналов при скоростях передачи до 8448 кбит/c, с малым отношением сигнал/шум (ОСШ) и компенсацией помехи с применением АЦП и ЦПОС отечественного или зарубежного производства при частоте дискретизации до 20-50 МГц [1, 2].
Моделирование проводится в несколько этапов:
1. Задание частотно-временных параметров сигнала, частоты дискретизации, длительности, времени анализа.
2. Результаты моделирования последовательностей информационных символов ФМ-2-сигнала rs, информационных символов ФМ-2-помехи ri и символа r0 случайной прерывистости излучения помехи показаны на рисунке 1.
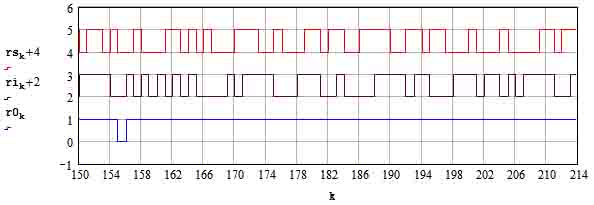
Рис. 1.
3. Моделирование ФМ-2-сигнала, случайно-прерывистой ФМ-2 помехи и белого шума при заданных энергиях сигнала и помехи на длительности символа сигнала отображено на рисунке 2.
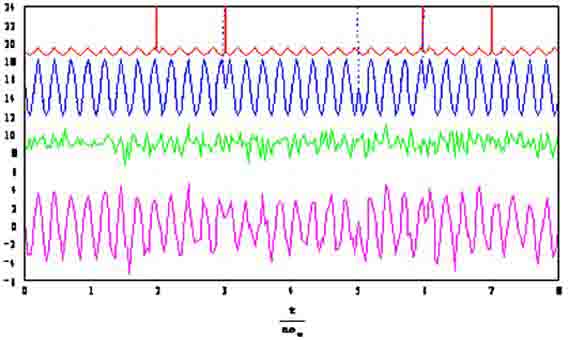
Рис. 2.
4. Статистическая оценка вероятности битовой ошибки Pb на выходе демодулятора, реализующего алгоритм компенсации помехи отражена в таблице 1.
Таблица 1.
|
Отношение помеха-сигнал (dB) |
Число ошибок без компенсатора (в среднем) |
Число ошибок с компенсатором (в среднем) |
Вероятность ошибки при приеме БЕЗ КОМПЕНСАТОРА |
Вероятность ошибки при приеме С КОМПЕНСАТОРОМ |
|
10 |
103,98 |
2,09 |
0,0508 |
0,0010 |
|
3 |
103,92 |
2,19 |
0,0507 |
0,0010 |
|
2,5 |
104,03 |
2,47 |
0,0508 |
0,0012 |
|
2 |
103,92 |
3,29 |
0,0507 |
0,0016 |
|
1,5 |
103,90 |
5,27 |
0,0507 |
0,0025 |
|
1 |
103,95 |
9,59 |
0,0558 |
0,0045 |
|
0,5 |
104,26 |
17,66 |
0,0559 |
0,0086 |
|
0 |
103,51 |
30,64 |
0,0559 |
0,0144 |
|
-0,5 |
103,34 |
47,92 |
0,0505 |
0,0234 |
|
-1 |
103,51 |
67,90 |
0,0505 |
0,0331 |
|
-1,5 |
103,51 |
86,96 |
0,0505 |
0,0425 |
|
-2 |
105,36 |
101,09 |
0,0514 |
0,0494 |
|
-2,3 |
104,16 |
104,03 |
0,0527 |
0,0508 |
|
-2,5 |
104,66 |
105,09 |
0,0510 |
0,0513 |
|
-2,6 |
104,14 |
104,66 |
0,0508 |
0,0511 |
|
-2,7 |
103,88 |
104,40 |
0,0507 |
0,0510 |
|
-2,8 |
104,10 |
104,39 |
0,0508 |
0,0510 |
|
-4 |
103,84 |
103,84 |
0,0507 |
0,0507 |
|
-7 |
93,17 |
92,97 |
0,0455 |
0,0454 |
|
-14 |
14,79 |
14,79 |
0,007 |
0,007 |
|
-20 |
3,5 |
3,5 |
0,001 |
0,001 |
5. Моделирование двух вариантов ремодуляции сигнала, очищенного от структурной помехи, на выходе компенсатора: ремодуляции по жестким решениям (рисунок 3) или мягким решениям (рисунок 4) о переданном сигнале.
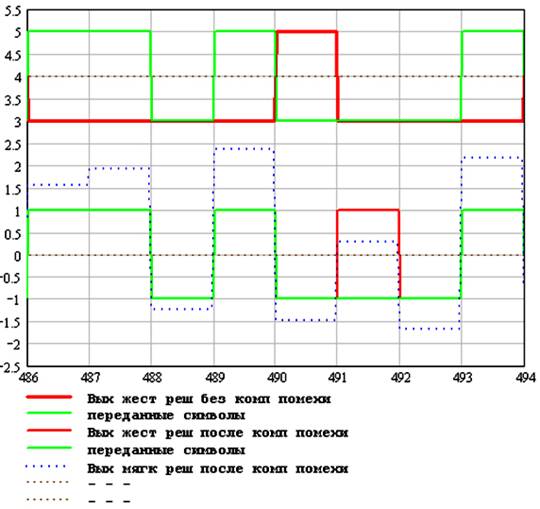
Рис. 3.
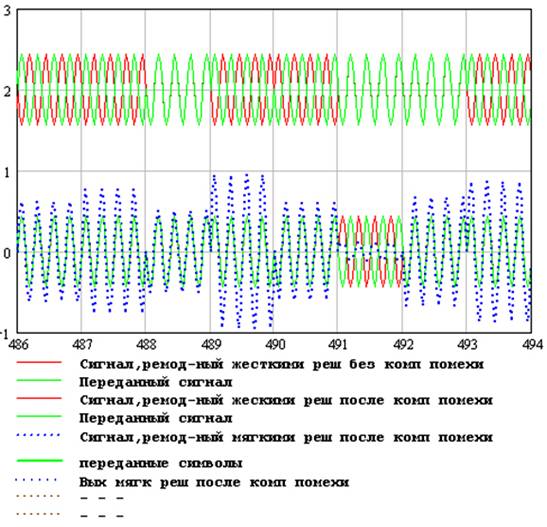
Рис. 4.
Из приведенных здесь теоретических обоснований следует, что в радиоканалах передачи данных при воздействии помехи может быть осуществлена теоретически сколь угодно эффективная, а на практике достаточно эффективная компенсация помехи в части полосы, значительно превышающей мощность полезного сигнала. Что крайне необходимо для радиоканалов передачи данных и обеспечения работоспособности радиотехнических систем [2].
Результирующие графики вероятности ошибочного приема в радиоканале без компенсации и с компенсацией приведены на рисунке 5. Представленные зависимости подтверждают теоретические выводы о возможности компенсации полной или значительной части энергии помехи в радиоканалах передачи данных.
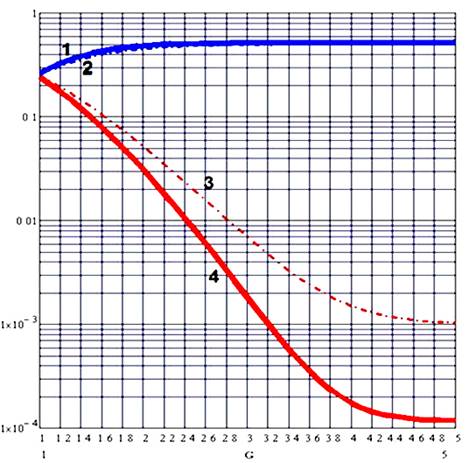
Рис. 5. Вероятность ошибочного приема в радиоканале без компенсации (кривые 1,2) и с компенсацией (кривые 3,4).
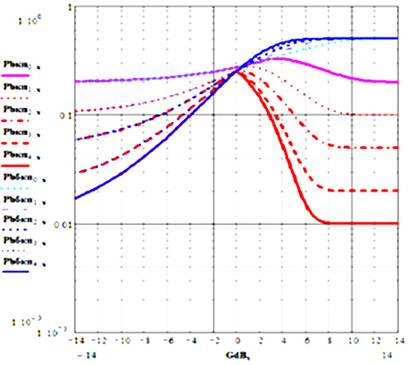
Рис. 6. Результирующие кривые вероятности ошибочного приема бита сигнала с компенсацией помех в части полосы (красные кривые) и без компенсации (синие кривые). Помеха в части полосы с вероятностью 0,9.
Выполненное сопоставление результатов теоретических расчётов помехоустойчивости оптимального алгоритма и результатов статистических испытаний на имитационной модели показывает хорошее совпадение полученных результатов, что приводит к следующим выводам:
1. Подтверждается корректность полученных математических соотношений расчёта помехоустойчивости.
2. Выполнена проверка теоретических положений, полученных аналитически, а также адекватности сделанных допущений. Базовые теоретические положения, положенные в основу компенсационного метода разделения сигналов, подтверждаются результатами имитационного моделирования.
3. Показана возможность практической реализации оптимальных и субоптимальных алгоритмов компенсации помех.
Литература
1. Бураченко Д.Л. Оптимальное разделение цифровых сигналов многих пользователей в линиях и сетях связи в условиях помех. – Л.: ВАС, 1990.- 302с.
2. Бураченко Д.Л., Ерохин В.Ф. Алгоритм разделения аддитивных неортогональных синхронных сигналов// Радиотехника. 1985. № 12. – с. 58-59. Деп. ЦНТИ «Информсвязь» 30.07. 1985. № 686. – 20с.
Поступила в редакцию 13.05.2011 г.