Wavelet analysis in Wavelet Transform Modulus Maxima Approach

 

Andrejs Pučkovs,

Economist, Mg. oec., PhD student of Riga Technical University.

 

This article is dedicated to eliminate financial time series multifractal research method which is based on both wavelet technique (for scalability research) and multifractal formalism. This multifractal research technique is called Wavelet Transform Modulus Maxima (here and further WTMM). This article should bring the light to the darkest sides of WTMM. This method is intended to be applicable for multifractal research of the most world stock indexes.

This article explore multifractal analysis in both: mathematical and programming languages in order to bring out clear and traceable exploration of all actions incorporated in financial time series multifractal analysis: mathematics should explore principles in multifractal research, Matlab programming code should be solid and reliable tool for financial time series multifractal analysis. The choice of Matlab programming language is substantiated especially with high development of Matlab programming language applicable in wavelet analysis. Programming exploration has one disadvantage: Matlab code use many internal functions, which are not traceable, but mathematical exploration is quite common and does not bring light on practical realization of algorithm (anyway it does not use fast working algorithms for estimation). Use of both languages should eliminate mentioned disadvantages. Key assets of this article are traceability and applicability of method. See exploration of WTMM approach next.

 

Wavelet Transform Modulus Maxima approach exploration

WTMM is a method for detecting the fractal dimension of a signal. More than this, the WTMM is capable of partitioning the time and scale domain of a signal into fractal dimension regions, and the method is sometimes referred to as a "mathematical microscope" due to its ability to inspect the multi-scale dimensional characteristics of a signal and possibly inform about the sources of these characteristics. The WTMM method uses continuous wavelet transform rather than Fourier transforms to detect singularities singularity – that is discontinuities, areas in the signal that are not continuous at a particular derivative. This method is useful when analyzing multifractal signals, that is, signals having multiple fractal dimensions. [[1]]

WTMM consist of following steps:

1)                  Data Mining and pre-processing (stock index data should be minded, stock index prices should be represented in log-scale);

такси в аэропорт домодедово

777rent.by

2)                  Wavelet analysis (Direct Continuous Wavelet Transform procedure should be done, after that Skeleton should be constructed;

3)                  Multifractal Formalism (Thermodynamics Partition function estimation (Fractal Partition Function calculation); Scaling exponent function estimation (Moment Generating Function calculation); Multifractal spectrum estimation).

Narration of WTMM approach is divided in two articles:

a)                   “Wavelet analysis in Wavelet Transform Modulus Maxima Approach” (current article where Data Mining and pre-processing block and Wavelet analysis block are narrated);

b)                  “Multifractal formalism in Wavelet Transform Modulus Maxima Approach” (article in current journal where Multifractal Formalism block is narrated).

The narration in current article is following: it begins from exploration of multifractal model of asset return (roots of financial time series multifractal analysis); next Data Mining and pre-processing block and Wavelet analysis blocks are narrated. All parts are explored in mathematical and programming languages consequently. Articles provide solid programming tool for multifractal spectrum estimation of various index or price data. This code imports data from ‘csv’ file and provides signal data, Direct Continuous Wavelet Transform (Direct CWT), Skeleton, Thermodynamics partition function, Local Scaling exponent () and Multifractal spectrum images in output. Also calculation matrixes are provided in ‘mat’ file type in output directory. This code is optional for WTMM approach exploration that brings out traceability and applicability of approach.

 

Multifractal Model of Asset Returns (MMAR)

There is one general assumption about stock price behavior. Expect the price of a stock or any other asset trading on the stock market is a multifractal process with fat tails and long-term dependency. Assumption about multifractal behavior of stock indexes goes to latest 90-th and based on Multifractal Model of Asset Return (MMAR), which was maintained by B. Mandelbrot, L. Calvet and A. Fisher. The Multifractal Model of Asset Returns (MMAR) provides the price of the asset by compounding a Fractional Brownian Model with a Trading Time. The Trading Time is a multifractal deformation of the time.

In accordance to MMAR stochastic process X(t) is called multifractal, if it has stationary increments and it satisfies:

                                                                                    (1)

where: X – stochastic process, time series; t – time; q – some positive number q = Q,; t - local scaling exponent; C – moment coefficient, that is independent from t. [[2]]

In order to satisfy equation and estimate financial time series data local scaling exponent t Wavelet Transform Modulus Maxima (WTMM) approach is used. WTMM is very advantageous approach for local scaling exponent estimation that allows to build the local scaling exponent function t (q) for both: positive and negative q values.

 

Data Mining and pre-processing block

Next fractal scaling exponent estimation is narrated. Stock index data is processed, using Matlab code:

 

clear all; clc; close all

%Predefine input and output directories

input = strcat('J:\Conferences&Publications\Jurnal2012Jul\indexes\');

output = strcat('J:\Conferences&Publications\Jurnal2012Jul\pictures\');

fileindex = strcat(input,'Fileindex.csv');

[name filename_] = textread(fileindex, '%s %s','delimiter',',');

len_ind_f = length(name);

savename = strcat(input,'metadata.mat'); save savename;

 

This code needs input [[3]] and output [[4]] directories declaration; data files should contain following fields: index code, date, adjusted close price. Data file (aex.csv) example is illustrated below:

^AEX;20120629;307.31

^AEX;20120628;297.22

 

This file should be placed into input directory. Also code requires index file in input directory, which is named (Fileindex.csv) and contain following fields: index name and index file name, example is illustrated below:

 

Amsterdam Exchange index,aex.csv

NIKKEI225 index,n225.csv

 

Data reading block is represented next:

 

for yy = 1:len_ind_f

%Load the data

input = strcat('J:\Conferences&Publications\Jurnal2012Jul\indexes\');

savename = strcat(input,'metadata.mat'); load savename

DATA = sortrows(dlmread(strcat(input,filename_{yy}),';',0,1));

%WTMM approach code [[5]]

end

 

For local scaling exponent estimation in case of financial time series, first at all time series or so called signal should be represented in log-scale, e.g. in natural logarithmic scale in accordance with formula:

                                                                                                        (2)

where:  - (pre-processed) signal; t – time at which the signal is recorded; P_close- market close price.

There is one question under discussion, which price in the market bears more information in it. Author considers close prices to be suitable for local scaling exponent estimation.

In Matlab code of this and other actions are represented below

 

%Define the stock index value space

X = log(DATA(:,2)); T = length(X); base = 8; %<- iteration step in CWT

D_max = base * floor(T/base);

X = X((length(X)-D_max+1):end); %<- signal from [start + eps] point to end

T = length(X);

 

Also time space needs to be taken in account, in order to provide various plots

 

%Define the time space and time labels

Dates = datenum(num2str(DATA(:,1)),'yyyymmdd');

labnum = 8; %number of labels in time ass

timestep = floor(T/labnum)-1;

Dates = datestr(Dates((length(Dates)-D_max+1):timestep:end), 'mm.yyyy');

clear D_max

 

Signal data (index price data) information is provided in plot by code:

 

%Define min/max margins of plot

minyy=(floor(log10(min(exp(X)))*10)/10);

maxyy=(ceil(log10(max(exp(X)))*10)/10);

loglinyy = linspace(minyy, maxyy, round((maxyy-minyy)/0.1)+1);

 

%Define min/max margins of plot

minyy=(floor(log10(min(exp(X)))*10)/10);

maxyy=(ceil(log10(max(exp(X)))*10)/10);

loglinyy = linspace(minyy, maxyy, round((maxyy-minyy)/0.1)+1);

 

%Plotting the signal

ii = 1; figure('Name',strcat(ii),'Color',[1 1 1]),

axes('YGrid','on',...

      'YTickLabel',loglinyy(1:2:length(loglinyy)),...

      'YTick',loglinyy(1:2:length(loglinyy)),'YTickMode','manual',...

      'XTickLabel',{Dates},...

      'XTick',1:timestep:T,'XTickMode','manual',...

      'XGrid','on', 'FontSize',10,...

      'FontWeight','bold',...

      'FontName','Times New Roman');

box('on'); hold('all');

plot(log10(exp(X)),'MarkerSize',4,'LineWidth',1.5)

axis([1 length(X) minyy maxyy])

title([name{yy}, sprintf('\n'),'Signal data'],'FontSize',16,'FontName','Times New Roman');

xlabel('Time, mm.yyyy','FontSize',16,'FontName','Times New Roman');

ylabel('Index value (in lg scale)','FontSize',16,'FontName','Times New Roman');

saveas(gcf,strcat(output,'Xplot',name{yy},'.jpg'))

clear minyy maxyy loglinyy

 

Illustrated data will used for signal fractal properties research

 

Wavelet analysis part

 

Direct Continuous Wavelet Transform (Direct CWT)

Standard Direct CWT procedure is realized by formula:

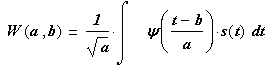                                                                  (3)

where: W(a,b) – wavelet coefficients; а – scaling parameter; b – shift parameter;  - signal; t – time at which the signal is recorded;  - mother wavelet ( or wavelet mother function).

 

Scaling parameter a

Scaling parameter a is representative for, but there is an opinion, that a scaling parameter used in WTMM approach is limited: . [[6]] Author consider the most informative a scaling parameters should be in interval , but in order to reduce calculation time, scaling parameters can be in interval . Consider, that it is not advisable to calculate wavelet coefficients for large a scales, which does not hold local maxima lines. That’s why maximal scales are dependent from local maxima lines. But local maxima lines are calculated using wavelet coefficients. For maximal scales detection author propose “spy” local maxima lines for some scales; algorithm is expressed by following Matlab code:

 

%Define minimal number and/or remaining percentage of lines

minlines = 1; %use not less then [minlines] lines

use_lines_percent = 0.85; %use [use_lines_percent] percent of lcmx lines

lines_100 = log(sum(round(localmax(cwt(X,1,'gaus2'))./Spy_jaggies(1,:))));

lines_0 = log(1); lines = cat(2,lines_0,lines_100); perc = [1 0];

percent_lines = round(exp(interp1(perc,lines,use_lines_percent)));

minlines = max(minlines,percent_lines); %use [use_lines_percent] percent of lines but not less [minlines]

clear lines_100 lines_0 perc lines percent_lines

 

i = 1; linenumbers = 100;

while true

      stpoint = i; enpoint = i+spyrows-1;

      W_spy = cwt(X,stpoint:enpoint,'gaus2');

      LCMX_spy = round(localmax(W_spy)./Spy_jaggies);

      LCMX_spy(:,1:enpoint) = zeros(spyrows,enpoint);

      LCMX_spy(:,(end-enpoint+1):end) = zeros(spyrows,enpoint);

      linenumbers = sum(sum(LCMX_spy))./spyrows;

      if (linenumbers <= minlines)

            depth = i;

            break

      else

            i = i+8*base;

      end

end

clear i minlines spyrows linenumbers stpoint enpoint Spy_jaggies LCMX_spy W_spy

           

The aim of this algorithm is to detect number of local maxima lines at selective scales. Scale number is increased (using some step) until number local maxima lines at current scale reaches some minimal limit (default minimal number of local maxima lines, or percent of local maxima lines at first scale (a = 1).

                                                                                 (4.1)

                                         (4.2)

where: Nlcmx_min - minimal limit (minimal number) of local maxima lines; N_def - default minimal number of local maxima lines; LcMx – wavelet skeleton function; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; P – percentage of local maxima lines considered.

In current algorithm minimal limit number is found, using exponential interpolation. Consider percentage of used local maxima lines at first scale (a = 1) is equal to 0, but percentage of used local maxima at last scale (first such scale, when number of local maxima lines reaches 1) is equal to 100; consequently minimal limit number, at certain percent of used local maxima lines, is found using exponential interpolation (by increasing scale, the number of local maxima lines decreases exponentially).

 

Shift parameter b and mother wavelet function y

Shift parameter b is limited , because shifting parameter b can not be greater than time t at which the signal is recorded. For detailed exploration of Direct CWT with numerical examples in MathCad see resource. [[7]]

Typical mother wavelet functions used for WTMM approach are MHAT (Mexican Hat) and Wave (first order Gauss wavelet).

Wave mother wavelet function is considered in formula:

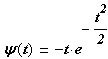                                                                                                         (5)

where:  - Wave mother wavelet function; t – time at which the signal is recorded.[[8]]

MHAT mother wavelet function is scripted following way:

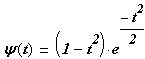                                                                                                (6)

where:  - Wave mother wavelet function; t – time at which the signal is recorded. [[9]]

There are many other mother wavelet functions, which are not described here because of complexity of exploration. Many authors consider better results of WTMM approach to be afforded using Wave mother wavelet function [[10]] [[11]]. Author considers Daubechies and Morlet mother wavelet function also to be appropriated for WTMM approach.

 Direct CWT provide wavelet coefficients W(a,b), which can be scripted in matrix form:

                               (7)

where: W(a,b) – wavelet coefficients; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length.

Since scaling parameter a_max is detected, Direct CWT is realized by code:

 

%Direct Continuous Wavelet Transform (CWT)

ii=ii+1; figure('Name',strcat(ii),'Color',[1 1 1]),

axes('XTickLabel',1:timestep:T,...

      'XTick',1:timestep:T,'XTickMode','manual',...

      'XGrid','on', 'FontSize',10,...

      'FontWeight','bold',...

      'FontName','Times New Roman');

box('on'); hold('all');

W = cwt(X,1:base:depth,'gaus2','abslvl'); %W - Wavelet coefficients matrix

[A_scales B_shifts] = size(W); a_scale = 1:base:depth;

log_scale = log(a_scale)';

axis([1 B_shifts 1 A_scales])

colormap(hot(64));

colorbar('location','EastOutside');

title([name{yy}, sprintf('\n'),'Continuous Wavelet Transform'],'FontSize',16,'FontName','Times New Roman');

xlabel('Time shifting, b','FontSize',16,'FontName','Times New Roman');

ylabel('Scales, a','FontSize',16,'FontName','Times New Roman');

saveas(gcf,strcat(output,'WT',name{yy},'.jpg'))

 

Also absolute wavelet coefficients matrix is used, which can be calculated using formula:

                       (8)

where:  - absolute wavelet coefficients matrix; W(a,b) – wavelet coefficients; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length.

 

Squared wavelet coefficients matrix also has sense in the context of wavelet skeleton. This matrix is calculated by formula:

                     (9)

where: - squared wavelet coefficients matrix; W(a,b) – wavelet coefficients; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length.

 

Usually wavelet coefficients (usually absolute wavelet coefficients matrix) are displayed as 3D graph projection on  space. Also in generated output plot wavelet coefficients are colored by its absolute values.

 

Skeleton construction

Wavelet Skeleton is aggregate of all Local Maxima Lines (LML) on each scale of Wavelet coefficients matrix. The idea of Skeleton matrix construction is to remove all wavelet coefficients in absolute wavelet coefficients matrix that are not maxima. In this way in Skeleton matrix stay only those absolute wavelet coefficients that belong to local maxima lines.

Next skeleton function (LcMx) is considered:

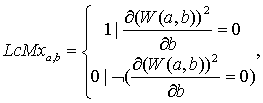                                                                   (10.1)

under the conditions:

                                                             (10.2)

where LcMx – wavelet skeleton function; W(a,b) – wavelet coefficients; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length.[[12]]

 

Wavelet Skeleton function can be scripted in matrix form by equation:

                (11)

where: LcMx – wavelet skeleton function; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length.

Usually Skeleton function in matrix form is calculated from squared wavelet coefficients matrix by formula:

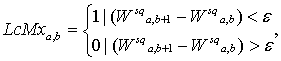                                                              (12.1)

under the conditions:

                                                       (12.2)

where: LcMx – wavelet skeleton function; - infinitesimal number (depended on calculation tolerance); - squared wavelet coefficients matrix; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length.

 

Skeleton matrix is a scope of all local maxima points that exist on each scale a. In fact skeleton function is a logical function, that has only two variables {0,1}. One is used if Skeleton matrix element is local maximum, zero – otherwise. Skeleton matrix 3D graph projection on  space resembles the map, where Local Maxima Lines (LML) are notched.

For skeleton function construction in Matlab environment is used build-in function localmax, whish is improved in Matlab code:

 

%Constructing the Skeleton function (or Local maxima lines)

for j=1:B_shifts

      Shift_jaggies(:,j) = j*ones(A_scales,1);% preparing for WTMM

end

clear j

 

delta = 1; %author defined iteration step for scales

for i = 1:floor(A_scales/delta);

      stpoint = delta*(i-1)+1; enpoint = delta*(i);

      LCMX(stpoint:enpoint,:) = localmax(W(stpoint:enpoint,:))./Shift_jaggies(stpoint:enpoint,:);

end

LCMX = round(LCMX);

 

Also corners  needs to be cleared (ignored) in skeleton. Consider wavelet coefficients on corners provide little information, consequently local maxima lines on corners should be removed [[13]], see formula:

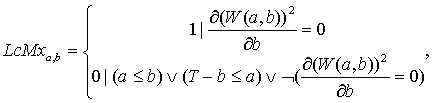                        (13.1)

under the conditions:

                                                             (13.2)

where: LcMx – wavelet skeleton function; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length.

This action is realized in Matlab code:

 

% Clear corners

for a0 = 2: A_scales

      LCMX(a0,1:base*a0) = zeros(1,base*a0);

      LCMX(a0,(end-base*a0+1):end)= zeros(1,base*a0);

end

clear a0

 

Plotting in Matlab environment is done by code:

 

% Ploting Skeleton

ii=ii+1; figure('Name',strcat(ii),'Color',[1 1 1],...

      'Colormap',[1 1 1; 0 0 1]),

axes('XTickLabel',1:timestep:T,...

      'XTick',1:timestep:T,'XTickMode','manual',...

      'YTickLabel',a_scale(1:10:length(a_scale)),...

      'YTick',1:10:length(a_scale),...

      'XGrid','on', 'FontSize',10,...

      'FontWeight','bold',...

      'FontName','Times New Roman');

box('on'); hold('all');

mesh(LCMX,'LineWidth',1.5);

axis([1 B_shifts 1 A_scales])

title([name{yy}, sprintf('\n'),'Wavelet Transform Modulus Maxima lines'],'FontSize',16,'FontName','Times New Roman');

xlabel('Time shifting, b','FontSize',16,'FontName','Times New Roman');

ylabel('Scales, a','FontSize',16,'FontName','Times New Roman');

saveas(gcf,strcat(output,'LCMX',name{yy},'.jpg'))

clear stpoint enpoint lcmx_ i Shift_jaggies delta

 

Skeleton matrix points generate ‘broken LML’. In order to afford quick results for “dirty” wavelet modulus maxima coefficients, use formula:

                                                                      (14.1)

under the conditions:

                                                        (14.2)

where: - “dirty” wavelet modulus maxima coefficients (fast algorithm); LcMx – wavelet skeleton function;  - absolute wavelet coefficients matrix; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length.

 

Fast algorithm of WTMM approach has one disadvantage, LML are broken that impacts Fractal Partition Function construction.

Latest methods in WTMM approach expect that Wavelet coefficients growth consequently on LML: increasing the scaling parameter a  almost everywhere wavelet coefficients increase . But in some points of broken LML, LcMx = 0, consiquently  = 0.

In order to prevent this case in WTMM approach are used procedures:

1)                  remove all “gaps” in LcMx matrix;

2)                  trace whether wavelet modulus coefficients on LML grow consequently with scaling parameter a:  almost everywhere .

Actually, last two procedures are the darkest sides of WTMM approach in literature. There is supremum formula for fractal partition function calculation.

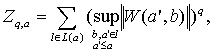                                                                               (15)

under the conditions:

where: Z – fractal partition function; W(a,b) – wavelet coefficients; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length; l - local maxima line (LML); L(a)– the scope of all local maxima lines, that exist on scale a; q – power indicator- some number, e.g. . See [[14]].

This formula suggests that for fractal partition function calculation should be taken those absolute wavelet coefficients, which:

1)                  lies on LML (LML l exist on ), and

2)                  maximum, which exist on LML (LML exist on )

3)                  in case, if decent absolute wavelet coefficient is not maximal on this LML, for calculation should be taken maximal point that exist on decent LML (LML exist on ).

In most literature this formula is not described analytically. Most programming codes that used for exploration of WTMM do not use “supremum algorithm” at all. Most of them use fast algorithm with “dirty” wavelet modulus maxima coefficients. [[15]]

Supremum algorithms in practice are very sophisticated, because skeleton does not contain local maxima lines in the true sense of the word: it has disconnected broken lines and single points. Actually it is difficult to assume how one skeleton point or broke line is related to another broke line or point. This is very hard programming task, which is arduous for narration in mathematic language. Instead of this, Matlab code is represented further.

After “dirty” wavelet modulus maxima coefficients are found, one more additional procedure should be established - probability normalization condition. This condition is directly concerned with Multifractal formalism procedure. Absolute wavelet coefficients normalization formula is shown next:

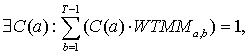                                                                     (16.1)

                                                                                              (16.2)

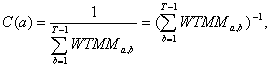                                                                 (16.3)

under the conditions:

                                                       (16.4)

where: - wavelet modulus maxima coefficients; C(a) – constant, dependent from scaling parameter a; а – scaling parameter; a_max – maximal scaling parameter; b – shift parameter; T – signal length.

 

Absolute wavelet coefficients normalization procedure usually is not implemented in WTMM approach, but author consider it should be implemented in order to afford analyzable results.

This procedure is realized in Matlab by script:

 

W_v = W; %<-Variable (not absolute) Wavelet coefficients

W = zeros(A_scales, B_shifts);

for i = 1:A_scales

      j = find(LCMX(i,:));

      W(i,j) = (1./sum(abs(W_v(i,j)),2))*abs(W_v(i,j));

end

 

Next Supremum algorithm is preceded. Last one consists of seven main steps:

 

1)                  Define matches (relations between single local maxima points)

 

% Supremum algorithm - start

F_relations = []; Single = [];

 

%Define matches (relations between single local maxima points)

for a = 1:A_scales

      %Define threshold

      b_indexes = find(LCMX(a,:)==1);

      % Define target at threshold

      for bb = 1:length(b_indexes)

            b = b_indexes(bb);

            target = W(a,b); %-<target

            %Define check area

            r = 1; r_max = 16; %<-define maximum and minimum radius

            while r <= r_max;

                  max_a = min(a+r,A_scales); min_a = max(a+1,1); %<- define bounds

                  max_b = min(b+r,B_shifts); min_b = max(b-r,1);

                  area = LCMX(min_a:max_a,min_b:max_b); %<- define area

                  [a_ar b_ar] = size(area);%<- define max bounds of area

 

                  %Check whether there is any point in cheek area

                  found = sum(sum(area));

                  if (found <1) && (r == r_max)

                        Single = cat(1,Single, cat(2,abs(W_v(a,b)),a,b));

                        break % in case if find matrix is empty and radius is maximal

 

                  elseif (found <1) && (r < r_max)

                        r = r+1;% increase radius in case if find matrix is empty but radius is not maximal

                  else

                  % Define positive case

                        % Calculate distance matrix

                        f_a = (min_a:max_a) - a; dist_a = repmat(f_a',1,b_ar);

                        f_b = (min_b:max_b) - b; dist_b = repmat(f_b,a_ar,1);

 

                        % Calculate distance-priority matrix

                        Dist_imp = ((dist_a.^2 + dist_b.^2).*area).^(1/2);

                        [f_row, f_col, f_val] = find(Dist_imp);

 

                        %Indicate element relation matrix

                        [S1a S1b] = size(f_val);

                        [S2a S2b] = size(repmat(target,found,1));

 

% REM: F_rel_cur organize relations matrix in folowing way:

%1column - Distance_value; 2column - Absolute_Wavelet_Coefficient_value;

%3column - First_point_a_coordinat; 5column - Second_point_a_coordinat;

%6column - Second_point_b_coordinat;

                        if(S1a == S2a)

                              F_rel_cur = sortrows(cat (2, f_val, repmat(target,found,1),repmat(a,found,1), repmat(b,found,1),(f_row+min_a-1), (f_col+min_b-1)));

 

                        elseif (S1b == S2a)

                              F_rel_cur = sortrows(cat (2, f_val', repmat(target,found,1),repmat(a,found,1), repmat(b,found,1),(f_row+min_a-1)', (f_col+min_b-1)'));

                        end

 

                        % Concatenating Paar Results

                        F_relations = cat(1,F_relations,F_rel_cur);

                        break

                  end

            end

      end

end

clear a b bb b_indexes target r max_a min_a max_b min_b area a_ar b_ar found f_a f_b f_row f_col f_val F_rel_cur cor_row dist_a dist_b r_max Dist_imp

clear S1a S1b S2a S2b S3a S3b S4a S4b S5a S5b S6a S6b

 

2)                  Define match conflict (one cell to more) and non conflict cases;

 

% Define match conflict (one cell to more) and non conflict cases

end_a_fil = sort(unique(F_relations(:,5))); end_b_fil = sort(unique(F_relations(:,6)));

Conflicts =[]; NonConflicts =[]; SolveConflicts = [];

 

for aa = 1:length(end_a_fil)

      for bb = 1:length(end_b_fil)

 

            %Coordinates

            a = end_a_fil(aa); b = end_b_fil(bb);

 

            %Comply whether is a conflict

            Check_ = find(F_relations(:,5)== a & F_relations(:,6) == b);

            found = length(Check_);

 

            %Conflict situation

            if (found > 1)%<- more one solution found

                  C_ = Check_;

                  N_ = [];

 

                  %Solve conflict

                  if (length(find(Check_(:,1) == min(Check_(:,1))))>1)

                        S_ = Check_((Check_(:,1) == min(Check_(:,1)) & Check_(:,2) == max(Check_(:,2))));

 

                  elseif (length(find(Check_(:,1) == min(Check_(:,1))))==1)

                        S_ = Check_((Check_(:,1) == min(Check_(:,1))));

                  else

                  end

 

            %Non conflict situation

            elseif (found == 1) %<- only one solution found

                  C_ = []; N_ = Check_; S_ = [];

            else

                  C_ = []; N_ = []; S_ = [];

            end

 

            %Matrix concatenation (merge all indexes together)

Conflicts = cat(1,Conflicts,C_);

            NonConflicts = cat(1,NonConflicts,N_);

            SolveConflicts = cat(1,SolveConflicts,S_);

      end

end

Solved = sort(cat(1,NonConflicts, SolveConflicts));

F_relations = F_relations(Solved,:); %<- removing comflicts

clear end_a_fil end_b_fil aa bb a b Check_ found C_ N_ S_ Conflicts NonConflicts SolveConflicts Solved

 

3)                  Creating Chains from pairs;

 

% Creating Chains from pairs

F_ = F_relations;

I = 1; j = 1; L = length(F_);

Chain_a =F_(1,3); Chain_b =F_(1,4);

Chains_a =[]; Chains_b =[];

Chains_mem_a = []; Chains_mem_b =[];

target_a = F_(j,3); target_b = F_(j,4);

 

while (L>1 )%<- number of row in F_ (F_relations) matrix

      while true

            partners_a = F_(:,3); partners_b = F_(:,4);

            r_partners_a = F_(:,5); r_partners_b = F_(:,6);

 

            k_s = find(partners_a == target_a & partners_b == target_b);

            K = length(k_s);

            if (isempty(k_s))

 

                  Chains_a = cat(1,Chains_a, {Chain_a});

                  Chains_b = cat(1,Chains_b, {Chain_b});

 

                  [Ch_mem_sz_a Dummy] = size(Chains_mem_a); %#ok<NASGU>

                  [Ch_mem_sz_b Dummy] = size(Chains_mem_b);

                  [L Dummy]= size(F_);

 

                  if (Ch_mem_sz_a >1 || Ch_mem_sz_b >1)

                        Chain_a = Chains_mem_a{Ch_mem_sz_a};

                        target_a = Chain_a(1,end);

                        Chain_a = Chain_a(1,1:end-1);

                        Chains_mem_a(Ch_mem_sz_a) = [];

 

                        Chain_b = Chains_mem_b{Ch_mem_sz_b};

                        target_b = Chain_b(1,end);

                        Chain_b = Chain_b(1,1:end-1);

                        Chains_mem_b(Ch_mem_sz_b) = [];

 

                  elseif L<1

                        break

                  else

                        target_a = F_(j,3);

                        target_b = F_(j,4);

                        Chain_a =target_a; Chain_b = target_b;

                  end

            break

 

      else

 

            temp_a = r_partners_a(k_s); temp_b = r_partners_b(k_s);

            k = 1;

                  Chain_a = cat(2,Chain_a,temp_a(k));

                  Chain_b = cat(2,Chain_b,temp_b(k));

 

                  target_a = temp_a(k);

                  target_b = temp_b(k);

 

                  for k = 2:K

                        Chain_mem_a = {cat(2,Chain_a,temp_a(k))};

                        Chain_mem_b = {cat(2,Chain_b,temp_b(k))};

 

                        Chains_mem_a = cat(1,Chains_mem_a,Chain_mem_a);

                        Chains_mem_b = cat(1,Chains_mem_b,Chain_mem_b);

                  end

 

                  F_(k_s,:) = [];

 

            end

      end

      [L Dummy]= size(F_);

end

 

clear ChEls_a ChEls_b ChNs_a ChNs_b Ch_mem_sz_a Ch_mem_sz_b Chain_a Chain_b Chain_mem_a Chain_mem_b Chains_mem_a Chains_mem_b F_ F_relations I K L NEls_a NEls_b Polynom Q S_a S_a_l S_a_w S_b S_b_l S_b_w T X ii j jj k k_s partners_a partners_b r_partners_a r_partners_b target_a target_b temp_a temp_b w_a w_b z

 

4)                  Chain interpolation (to fill missing wavelet coefficients on WTMM line);

 

%Chain interpolation (to fill missing wavelet coefficients on WTMM line)

ChNs = length(Chains_a);

for ii = 1:ChNs

      a_row_ = cell2mat(Chains_a(ii));% - existed a in chains

      b_row_ = cell2mat(Chains_b(ii));% existed b in chains

      if length(a_row_)>length(unique(a_row_))

            a_rowtarget = unique(a_row_);

            jr =[];

            for ind_ra = 1:length(a_rowtarget)

                  temp_jr = find(a_row_ == a_rowtarget(ind_ra));

                  temp_jr = temp_jr(1);

                  jr = cat(2,jr,temp_jr);

            end

            a_row_ = a_row_(jr);

            b_row_ = b_row_(jr);

      end

 

      int = a_row_(1): a_row_(end);% -<integer vector for a

      Chains_i_a(ii,1) = {interp1(a_row_,a_row_,int)};

      Chains_i_b(ii,1) = {round(interp1(a_row_,b_row_,int))};

end

clear Chains_a Chains_b a_row_ alpha b_row_ ii int filename_ jr

 

5)                  Adding points to LCMX map (on line gaps);

 

%Adding points to LCMX map (on line gaps)

LCMX_sup = zeros(size(LCMX));

for ii = 1:ChNs

      Cur_ch_a = cell2mat(Chains_i_a(ii,1));

      Cur_ch_b = cell2mat(Chains_i_b(ii,1));

      for jj = 1:length(Cur_ch_a)

            % Creating LCMX map

            Cur_ch_a_ind = round(Cur_ch_a(jj));

            Cur_ch_b_ind = round(Cur_ch_b(jj));

            LCMX_sup(Cur_ch_a_ind, Cur_ch_b_ind) = 1;

 

            % Creating (adjusted) Supremum Wavelet coefficients in Wavelet matrix

            Cur_chain_val(ii,jj) = abs(W_v(Cur_ch_a_ind,Cur_ch_b_ind));

            Cur_chain_val(ii,jj) = max(Cur_chain_val(ii,1:jj));

            W_sup(Cur_ch_a_ind, Cur_ch_b_ind) = Cur_chain_val(ii,jj);

      end

      Cur_ch_a = []; Cur_ch_b = []; Cur_chain_val = [];

end

clear Cur_ch_a Cur_ch_b Cur_ch_a_ind Cur_ch_b_ind Cur_chain_val jj

 

6)                  Adding single points to LCMX map;

 

%Adding single points to LCMX map

for ind = 1: length(Single)

      val = Single(ind,1);

      aa = Single(ind,2);

      bb = Single(ind,3);

      LCMX_sup(round(aa),round(bb)) = 1;

      W_sup(round(aa),round(bb)) = val;

End

 

7)                  Changing of variables (at the end)

 

%Changing of variables (at the end)

LCMX = LCMX_sup; W = W_sup;

clear aa bb val ind ChEls ChNs Chains_i_a Chains_i_b Chains_int_a Chains_int_b Chains_int_values

clear Ch_vector_a Ch_vector_b Ch_vector_val LCMX_sup W_sup Single

% Supremum algorithm - end

 

At the end, Wavelet matrix is replaced with Wavelet skeleton matrix that includes wavelet supremum wavelet coefficients. After this, Multifractal formalism (MfF) should be applied for WTMM approach realization (see “Multifractal formalism in Wavelet Transform Modulus Maxima Approach”).

 

Bibliography

 

1.                   http://chaos.sgu.ru. Мультифрактальный анализ сложных сигналов. [http://chaos.sgu.ru/~pavlov/papers/r078c.pdf] (Accessed 1 July. 2012.).

2.                   http://chaos.sgu.ru. Мультифрактальный анализ сложных сигналов. [http://chaos.sgu.ru/~pavlov/papers/r078c.pdf] (Accessed 1 July. 2012.).

3.                   http://disp.ee.ntu.edu.tw. A Tutorial of the Wavelet Transform. [disp.ee.ntu.edu.tw/tutorial/WaveletTutorial.pdf] (Accessed 1 April 2012.).

4.                   http://en.wikipedia.org. Wavelet transform modulus maxima method. [http://en.wikipedia.org/wiki/Wavelet_transform_modulus_maxima_method] (Accessed 1 July. 2012.).

5.                   http://users.math.yale.edu. A Multifractal Model of Asset Returns. [http://users.math.yale.edu/mandelbrot/web_pdfs/Cowles1164.pdf] (Accessed 1 July. 2012.).

6.                   http://web.eecs.umich.edu. Mallat's fast wavelet algorithm: recursive computation ofcontinuous-time wavelet coefficients. [http://web.eecs.umich.edu/~aey/eecs551/lectures/mallat.pdf] (Accessed 1 July. 2012.).

7.                   http://window.edu.ru. Введение в вейвлет-преобразования. [http://window.edu.ru/resource/328/29328/files/nstu68.pdf] (Accessed 1 July. 2012.).

8.                   http://www.cinc.org. A Comparison of Continuous Wavelet Transform and Modulus Maxima Analysis of Characteristic ECG Features. [http://www.cinc.org/archives/2005/pdf/0755.pdf]. (Accessed 1 July. 2012.).

9.                   http://www.scholarpedia.org. Wavelet-based_multifractal_analysis. [http://www.scholarpedia.org/article/Wavelet-based_multifractal_analysis] (Accessed 1 July. 2012.).

10.               http://www.wstein.org. Multifractal formalism for fractal signals: The structure-function approach versus the wavelet-transform modulus-maxima method. (Accessed 1 July. 2012.).

 

Поступила в редакцию 16.07.2012 г.