Multifractal formalism in Wavelet Transform Modulus Maxima Approach
Andrejs Pučkovs,
Economist, Mg. oec., PhD student of Riga Technical University.
This article is dedicated to eliminate financial time series multifractal research method which is based on both wavelet technique (for scalability research) and multifractal formalism. This multifractal research technique is called Wavelet Transform Modulus Maxima (here and further WTMM). This article should bring the light to the darkest sides of WTMM. This method is intended to be applicable for multifractal research of the most world stock indexes.
This article explore multifractal analysis in both: mathematical and programming languages in order to bring out clear and traceable exploration of all actions incorporated in financial time series multifractal analysis: mathematics should explore principles in multifractal research, Matlab programming code should be solid and reliable tool for financial time series multifractal analysis. The choice of Matlab programming language is substantiated especially with high development of Matlab programming language applicable in wavelet analysis. Programming exploration has one disadvantage: Matlab code use many internal functions, which are not traceable, but mathematical exploration is quite common and does not bring light on practical realization of algorithm (anyway it does not use fast working algorithms for estimation). Use of both languages should eliminate mentioned disadvantages. Key assets of this article are traceability and applicability of method. See exploration of WTMM approach next.
Wavelet Transform Modulus Maxima approach exploration
WTMM is a method for detecting the fractal dimension of a signal. More than this, the WTMM is capable of partitioning the time and scale domain of a signal into fractal dimension regions, and the method is sometimes referred to as a "mathematical microscope" due to its ability to inspect the multi-scale dimensional characteristics of a signal and possibly inform about the sources of these characteristics. The WTMM method uses continuous wavelet transform rather than Fourier transforms to detect singularities singularity – that is discontinuities, areas in the signal that are not continuous at a particular derivative. This method is useful when analyzing multifractal signals, that is, signals having multiple fractal dimensions. [[1]]
WTMM consist of following steps:
1) Data Mining and pre-processing (stock index data should be minded, stock index prices should be represented in log-scale);
2) Wavelet analysis (Direct Continuous Wavelet Transform procedure should be done, after that Skeleton should be constructed;
3) Multifractal Formalism (Thermodynamics Partition function estimation (Fractal Partition Function calculation); Scaling exponent function estimation (Moment Generating Function calculation); Multifractal spectrum estimation).
Narration of WTMM approach is divided in two articles:
a) “Wavelet analysis in Wavelet Transform Modulus Maxima Approach” (article in current journal where Data Mining and pre-processing block and Wavelet analysis block are narrated);
b) “Multifractal formalism in Wavelet Transform Modulus Maxima Approach” (current article where Multifractal Formalism block is narrated).
Narration in current article is following: it begins from exploration of Thermodynamics Partition function estimation next Scaling exponent function and Multifractal spectrum estimations are narrated. All parts are explored in mathematical and programming languages consequently. Articles provide solid programming tool for multifractal spectrum estimation of various index or price data. This code import data from ‘csv’ file and provides signal data, Direct Continuous Wavelet Transform (Direct CWT), Skeleton, Thermodynamics partition function, Local Scaling exponent () and Multifractal spectrum images in output. Also calculation matrixes are provided in ‘mat’ file type in output directory. This code is optional for WTMM approach exploration that brings out traceability and applicability of approach.
Multifractal Formalism part
Multifractal Formalism (MfF) procedure is a part of WTMM approach and consists of following steps:
1. Thermodynamics Partition function estimation (Fractal Partition Function calculation);
2. Scaling exponent function estimation (Moment Generating Function calculation);
3. Multifractal spectrum estimation.
Here and further the MfF algorithm is considered:
1. Thermodynamics Partition function estimation
Thermodynamics Partition function is based on ‘generalized’ partition function consideration. Wavelet modulus maxima coefficients are akin to probability measure in so called ‘generalized’ partition function.
Thermodynamics Partition function is scripted next by formula:
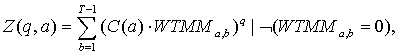(1)
where: Z(q,a) – thermodynamics partition function; 
- wavelet modulus maxima coefficients; C(a)
– constant, dependent from scaling parameter a; à – scaling
parameter; q – exponent number, for example
.
Thermodynamics Partition function is a
function of two arguments - scaling parameter a and power
argument q. Power argument q is the set of
zero-mean numbers (exponent number, for example in interval), that indicate presence of
wavelet modulus maxima coefficients of different values: the presence of
relative small wavelet modulus maxima coefficients 
is detectable with large Z
values 
in
case of negative q values
; and the presence of relative large
wavelet modulus maxima coefficients is detectable with large Z values in case of positive q
values
.
Scaling parameter a is an argument of Thermodynamics Partition function, that, by its nature, is the scaling “etalon” for Thermodynamics Partition function value. Interdependence between Thermodynamics Partition function value and scaling parameter a discovers the scalability of signal. That is a key moment in all WTMM approach.
Thermodynamics Partition function is finite
if wavelet modulus maxima coefficients are not equal to zero: 
. In order to satisfy
condition all zero coefficients should be neglected in wavelet modulus maxima
matrix WTMM. The origin of zero coefficients in wavelet modulus maxima matrix
is in LcMx wavelet skeleton function – all elements in Skeleton matrix
that are not local maximums are zero valued elements. Having in view previous
statement Thermodynamics Partition function can be scripted by formula:
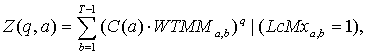(2)
where: Z(q,a) – thermodynamics partition function; - wavelet modulus maxima coefficients; LcMx
– wavelet skeleton function; C(a) – constant, dependent from
scaling parameter a; à – scaling parameter; q
– exponent number, for example.
Thermodynamics Partition function is estimated via Matlab code:
i = 3;
%may be needs correction of tau scaling spectrum because (~8 rows instable)
cor_row =8; % by A_scales = (base * scale)
%Thermodynamics partition function
q = linspace(-5,5,101); nq = length(q);
for kk=cor_row:A_scales, %#ok<ALIGN>
k = kk-cor_row+1;
j = find(LCMX(kk,:));
if ~isempty(j),
C = abs(W(kk,j));
for i=1:nq,
z(i,k) = sum(C .^ q(i));
end
else
for i=1:length(q),
z(i,k) = eps.^q(i);
end
end
end
clear kk k i j C tau[[2]]
After that, Thermodynamics Partition function is plotted. Thermodynamics Partition function is 3D function, that is very complex for illustration. Actually this function can be displayed easy in log-scale. Plotting is done by Matlab script:
Q = q';Z_log = log(z);
ii=ii+1; figure('Name',strcat(ii),'Color',[1 1 1])
axes('XGrid','on',...
'YGrid','on',...
'XTickLabel',a_scale(1:10:length(a_scale)),...
'XTick',1:10:length(a_scale),...
'YTickLabel',Q(1:10:length(Q)),...
'YTick',1:10:length(Q),...
'FontSize',10,...
'FontWeight','bold',...
'FontName','Times New Roman');
view([145 35]);
box('on'); hold('all');
mesh(Z_log);
axis([1 A_scales 1 nq])
title([name{yy}, sprintf('\n'),'Thermodinamics partition function'],'FontSize',16,'FontName','Times New Roman');
xlabel('Scales, a','FontSize',16,'FontName','Times New Roman');
ylabel('q values','FontSize',16,'FontName','Times New Roman');
zlabel('Function value (in log scale)','FontSize',16,'FontName','Times New Roman');
saveas(gcf,strcat(output,'Z',name{yy},'.jpg'))
clear Zf K Kernel logZ Z_log
In order to discover the scalability of signal, next Scaling exponent function is considered.
Scaling exponent function estimation
Scaling exponent function is one argument function, that indicate Interdependence between Thermodynamics Partition function Z and scaling parameter a. Scaling exponent function is calculated as the slope between Thermodynamics Partition function Z and scaling parameter a by formula:
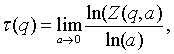(3)
where: Z(q,a) – thermodynamics partition function; t - local
scaling exponent; à – scaling parameter; q – exponent
number, e.g..
See [[3]]
Last formula can be expanded to:
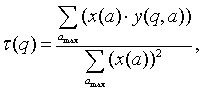(4.1)
where:
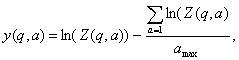(4.2)
where:
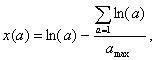(4.3)
under the conditions:
(4.4)
exploration: t - local scaling exponent; Z(q,a) – thermodynamics
partition function; à – scaling parameter; amax
– maximal scaling parameter; q –exponent number, e.g..
Scaling exponent function is non-decreasing function that indicates the scalability of signal. There are two main cases: mono- and multifractal. In monofractal case the scaling exponent function is linear. In multifractal case, the scaling exponent function is everywhere convex.
There is one interesting property to be considered with Scaling exponent function:
(5)
where: t - local scaling exponent.
This condition is essential for Multifractal spectrum estimation. Actually this condition is satisfied not in all cases, for example in case of financial time series analysis. For that author offers following formula:
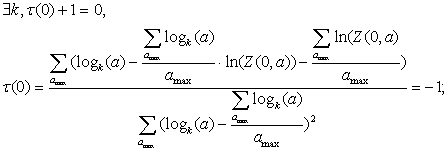(6.1)
let:
(6.2)
then:
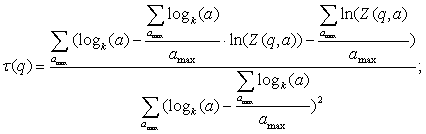(6.3)
or:
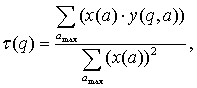(6.4)
where:
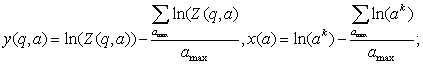(6.5)
under the conditions:
(6.6)
exploration: t - local scaling
exponent; Z(q,a) – thermodynamics partition function; à
– scaling parameter; amax – maximal scaling
parameter; q –exponent number, e.g..
This transformation is beneficial for
Scaling exponent function estimation in case if 
. After transformation this essential
condition is satisfied.
In Matlab environment this algorithm is realized by script:
%Local scaling exponent (tau) calculation
tau = zeros(nq,1);
for kq =1:nq,
y = log(z(kq,:)); y = y-mean(y);
x = log(a_scale(cor_row:end)); x = x-mean(x);
tau(kq) = sum(y.*x) / sum(x.*x);
end [[4]]
Local Scaling Exponent normalization is represented next:
% Adjusting tau
k = -tau((q==min(abs(q - 0))));
an_scale = a_scale.^(k);
for kq =1:nq,
y = log(z(kq,:)); y = y-mean(y);
x = log(an_scale(cor_row:end)); x = x-mean(x);
tau(kq) = sum(y.*x) / sum(x.*x);
end
clear x y kq k an_scale q cor_row
After that, local scaling exponent function is plotted by Matlab code:
ii=ii+1; figure('Name',strcat(ii),'Color',[1 1 1])
axes('YGrid','on',...
'XGrid','on',...
'FontWeight','bold',...
'FontName','Times New Roman');
box('on'); hold('all');
plot(Q,tau,'MarkerSize',4,'LineWidth',1.5);
axis([min(Q) max(Q) min(tau) max(tau)])
title([name{yy}, sprintf('\n'),'Scaling exponent (tau)'],'FontSize',16,'FontName','Times New Roman');
xlabel('q values','FontSize',16,'FontName','Times New Roman');
ylabel('Scaling exponent','FontSize',16,'FontName','Times New Roman');
saveas(gcf,strcat(output,'tau',name{yy},'.jpg'))
clear x y kq
Estimated scaling exponent function is used for MMAR stochastic process simulation that satisfies equation (1).
2. Multifractal spectrum function estimation
Multifractal Formalism use multifractal spectrum for detailed fractal analysis of the signal. Multifractal spectrum function shows the scope of all fractal measures. Multifractal spectrum function is calculated from Scaling exponent function via Legendre transformation by formula:
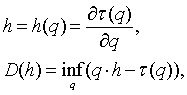(7)
where: D – multifractal spectrum; h – Holder
exponent; t - local scaling exponent; q – exponent number,
e.g..[5]
In case of monofractal signal Multifractal spectrum function transforms to single point (h, 1), but In case of multifractal signal Multifractal spectrum function is bell-shaped function, which branches are directed downwards. Multifractal spectrum function maxima point is (h, 1). In both cases: mono- and multifractal h is Holder exponent, which indicates most typical measure of fractal.
Multifractal spectrum is estimated in and plotted Matlab by script:
%Holder exponent (h) spectrum estimation
alpha = diff(tau)./diff(Q);
f=((Q(1:(end-1)).*(alpha))-tau(1:(end-1)));
ii=ii+1; figure('Name',strcat(ii),'Color',[1 1 1])
createfigure2(alpha,f,name{yy}) %for simplicity can be used: plot(alpha,f)
Polynom = polyfit(alpha,f,4);
saveas(gcf,strcat(output,'Alpha',name{yy},'.jpg'))
clear d_pre d_post max_alpha k_alpha half hind n_alpha nq depth D_max base ii Dummy
savefile = strcat(output, name{yy},'.mat'); save (savefile)
close all; clear all;
Multifractal spectrum can be approximate via polynomial. Multifractal spectrum is approximation with 4-th degree polynomial is scripted by formula:
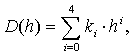(8)
where: D – multifractal spectrum; h – Holder exponent; k – polynomial coefficients; i - polynomial coefficient index i =0,1,…4. [[6]]
Multifractal spectrum is approximation by Matlab code is represented next:
Polynom = polyfit(alpha,f,4);
At the end, in the output directory are located signal data, Direct Continuous Wavelet Transform (Direct CWT), Skeleton, Thermodynamics partition function, Local Scaling exponent (t) and Multifractal spectrum images in ‘jpg’ format. Also calculation matrixes are provided in ‘mat’ file type in output directory.
For detailed application of WTMM approach, see article “Stock indexes multifractal analysis” in current journal.
Bibliography
1. Êîðîëåíêî, Ìàãàíîâà, Ìåñíÿíêèí. Íîâàöèîííûå ìåòîäû àíàëèçà ñòîõàñòè÷åñêèõ ïðîöåññîâ è ñòðóêòóð â îïòèêå. Ôðàêòàëüíûå è ìóëüòèôðàêòàëüíûå ìåòîäû, âåéâëåò-ïðåîáðàçîâàíèÿ. – Ì.: 2004 - 81 ñòð. – 41. ñòð.
2. Øåëóõèí. Ìóëüòèôðàêòàëû. Èíôîêîìóíèêàöèîííû ïðèëîæåíèÿ. – Ì.: Ãîðÿ÷àÿ ëèíèÿ Òåëåêîì, 2011.ã. 576 ñòð. – 24. ñòð.
3. http://en.wikipedia.org. Polynomial [http://en.wikipedia.org/wiki/Polynomial]. (Accessed 1. July 2012).
4. http://en.wikipedia.org. Wavelet transform modulus maxima method. [http://en.wikipedia.org/wiki/Wavelet_transform_modulus_maxima_method] (Accessed 1 July. 2012.).
5. http://www-stat.stanford.edu. FracScalExp - Calculate Moment Generating Function. [http://www-stat.stanford.edu/~wavelab/Wavelab_850/download.html] (Accessed 1 July. 2012.).
6. http://www-stat.stanford.edu. Fractal Partition Function based on wavelet modulus maxima. [http://www-stat.stanford.edu/~wavelab/Wavelab_850/download.html] (Accessed 1 July. 2012.).
Ïîñòóïèëà â ðåäàêöèþ 16.07.2012 ã.
[1] http://en.wikipedia.org. Wavelet transform modulus maxima method. [http://en.wikipedia.org/wiki/Wavelet_transform_modulus_maxima_method] (Accessed 1 July. 2012.).
[2] http://www-stat.stanford.edu. Fractal Partition Function based on wavelet modulus maxima. [http://www-stat.stanford.edu/~wavelab/Wavelab_850/download.html] (Accessed 1 July. 2012.).
[3] Êîðîëåíêî, Ìàãàíîâà, Ìåñíÿíêèí. Íîâàöèîííûå ìåòîäû àíàëèçà ñòîõàñòè÷åñêèõ ïðîöåññîâ è ñòðóêòóð â îïòèêå. Ôðàêòàëüíûå è ìóëüòèôðàêòàëüíûå ìåòîäû, âåéâëåò-ïðåîáðàçîâàíèÿ. – Ì.: 2004 - 81 ñòð. – 41. ñòð.
[4] http://www-stat.stanford.edu. FracScalExp -- Calculate Moment Generating Function. [http://www-stat.stanford.edu/~wavelab/Wavelab_850/download.html] (Accessed 1 July. 2012.).
[5] Øåëóõèí. Ìóëüòèôðàêòàëû. Èíôîêîìóíèêàöèîííû ïðèëîæåíèÿ. – Ì.: Ãîðÿ÷àÿ ëèíèÿ Òåëåêîì, 2011.ã. 576 ñòð. – 24. ñòð.
[6] http://en.wikipedia.org. Polynomial [http://en.wikipedia.org/wiki/Polynomial]. (Accessed 1. July 2012).