Исследование статистических свойств искажений частотных коэффициентов ДКП матрицы в условиях воздействия на изображение JPEG-сжатия

Коваленко Михаил Павлович,

аспирант, инженер-программист отдела СПМО МОУ

«Институт инженерной физики».

Цель работы – постановка и анализ результатов эксперимента, проводимого с целью выявления статистических свойств искажений частотных коэффициентов ДКП матрицы при Jpeg-сжатии изображения.

The goal of this article is staging and analysis of the results of the experiment conducted to identify the statistical properties of the DCT coefficients’ distortions in images after Jpeg-compression.

Ключевые слова: стеганография, алгоритм частотной области, коэффициент матрицы дискретно-косинусного преобразования, искажение, математическое ожидание, среднеквадратическое отклонение, Jpeg-сжатие.

Введение

Стеганографические алгоритмы, производящие встраивание скрываемой информации в частотную область изображений, получили широкое распространение в силу некоторых выгодных отличий от остальных стеганографических алгоритмов. К сильным сторонам данного вида алгоритмов, прежде всего, следует отнести возможность встраивать информацию в изображения-контейнеры, сжатые форматом JPEG, который является одним из наиболее распространенных форматов хранения и передачи мультимедиаконтента на сегодняшний день. Также к преимуществам данного вида алгоритмов можно отнести и достаточно хорошую устойчивость к различного рода внешним воздействиям или атакам на изображение-контейнер.

Частотные свойства матрицы ДКП коэффициентов

В основе большинства стеганографических алгоритмов частотной области лежит дискретно-косинусное преобразование (ДКП). Такие алгоритмы предварительно разбивают исходное изображение-контейнер на блоки, как правило, размером 8×8 пикселей, в дальнейшем подвергающиеся ДКП, результатом которого является матрица коэффициентов, представленная на рис. 1.

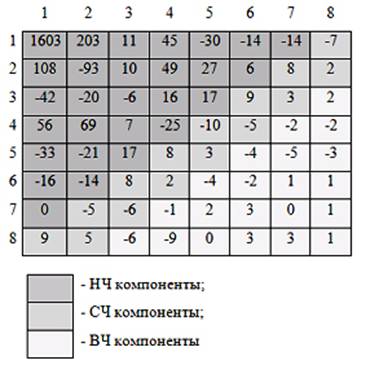
Рис. 1. Матрица ДКП коэффициентов.

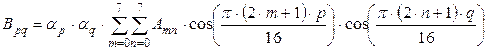,       (1)

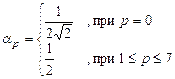 и 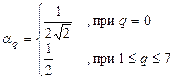,                                     (2-3)

где 0 £ p £ 7; 0 £ q £ 7; A – матрица, подвергаемая ДКП; B – матрица ДКП коэффициентов.

В ДКП матрице, вычисляемой для блоков размером 8×8 пикселей по формулам 1-3, коэффициенты низкочастотных компонент располагаются ближе к верхнему левому углу, в то время как коэффициенты высокочастотных компонент сгруппированы в правой нижней части матрицы (рисунок 1). Низкочастотные коэффициенты содержат преобладающую часть энергии изображения, в то время как высокочастотные компоненты наиболее уязвимы для внешних воздействий [1]. Поэтому авторы большинства алгоритмов считают пригодными для встраивания только среднечастотные коэффициенты. Но на сколько эти коэффициенты подвержены, например, Jpeg-сжатию изображения? Поиску ответа на данный вопрос и посвящена данная работа.

Анализ статистических свойств искажений частотных коэффициентов ДКП матрицы в условиях воздействия на изображение Jpeg-сжатия

Для среднечастотных коэффициентов ДКП матрицы на базе 82 изображений (общее число ДКП-блоков равно 1 124 837) определим математические ожадания и разбросы величин искажений, вносимых в изображения при их Jpeg-сжатии, осуществляемом при помощи пакета программ StirMark Benchmark 4.0.129.

Продемонстрируем уровень вносимых искажений на примере.

Рис. 2. Фрагмент исходного изображения.

Рис. 3. Фрагмент изображения после Jpeg-сжатия (параметр «JPEG Quality level» равен 90).

Рис. 4. Фрагмент изображения после Jpeg-сжатия (параметр «JPEG Quality level» равен 10).

Таблица 1.

Статистические свойства частотных коэффициентов.

В таблице 1 через  обозначен номер частотного коэффициента,  – математическое ожидание величины его искажения,  – среднеквадратическое отклонение величины его искажения,  – вероятность (в %) того, что величина искажения окажется в диапазоне от  до .

Выводы

Итак, согласно полученным данным математические ожидания искажений частотных коэффициентов лежат в интервале от – 0.0438641 до 0.0596889.

На основании представленных данных можно сделать вывод, что при внедрении информации частотные коэффициенты ДКП матрицы следует изменять на величины не менее трех среднеквадратических отклонений их искажений, а именно на величину из интервала от 4 до 37 при условии Jpeg-сжатия изображения в зависимости от его степени.

Литература

1. Конахович Г.Ф., Пузыренко А.Ю. Компьютерная стеганография: Теория и практика. – М.: МК-Пресс, 2006. – 283 с.

Поступила в редакцию 14.02.2012 г.