Статистические критерии для оценки энтропии

Ставер Елена Владимировна,

магистрант физико-математических наук.

Научно-образовательный центр «Современные системы обучения».

Моя основная цель – получить случайную последовательность. Можно сделать период последовательности длинным и при практических применениях он не будет повторяться [1]. Это важный критерий, но нет гарантии того, что последовательность будет использоваться в реальных приложениях.

Теоретическая статистика предоставляет количественные меры случайности. Существует теоретически бесконечное число критериев, которые можно использовать для проверки последовательности на случайность.

Если критерии T₁, T₂,…T_n подтверждают, что последовательность ведет себя случайным образом, это еще не означает, что проверка T_n+1-го критерия будет успешной [1]. Но каждая успешная проверка дает все больше уверенности в случайности последовательности. Обычно к последовательности применяется множество статистических критериев, и если она удовлетворяет этим критериям, то последовательность считается случайной.

Критерий на равномерное распределение

Этот критерий является важным методом проверки качества линейных конгруэнтных ГСЧ [1]. Испытанием для проверки случайности будет последовательность, связанная со свойствами распределений t последовательных элементов последовательности. Если задана последовательность U_n с периодом m, то для построения критерия необходимо изучить множество всех m точек

{(U_n,U_n+1, … U_n+t-1) | 0 ≤n≤m}                                                                                (1)

в t-мерном пространстве. Задана линейная конгруэнтная последовательность {Хо,а,с,m) с максимальным периодом длиной. В последнем случае прибавляется точка (0, 0, ...,0) к множеству (1), чтобы всегда было ровно m точек. При таком предположении (1) переписываем выражение:

                                                   (2)

Представляет собой элемент, следующий за x. Здесь рассматривается лишь множество всех таких точек в t-мерном пространстве, а не порядок, в котором они генерируются.

Критерий перестановок

Выборка является равномерно распределенной, после перемешивания она должна удовлетворять начальным критериям. Ожидается, что первоначальная оценка результатов будет основываться на «перемешанных» выборках, так как результаты, полученные на оригинальной выборке, либо необычайно высоки, либо низки, т.е. являются неточными [1]. Если выборка не является равномерно распределенной, то некоторые оценочные результаты могут сильно отличаться на оригинальной и «перемешанной» выборке.

Проверка по критерию «хи-квадрат»

Критерий «хи-квадрат» — является важным методом, который используется наряду с другими критериями. Для моего случая проверка по данному критерию позволяет узнать, насколько созданный мной реальный ГСЧ будет удовлетворять требованию равномерного распределения [1].

Частотная диаграмма реального ГСЧ представлена на рисунке 1. Закон распределения эталонного ГСЧ равномерный, то вероятность p_i попадания чисел в i-ый интервал равна p_i = 1/k. В каждый из k интервалов попадет ровно по p_i · N чисел.

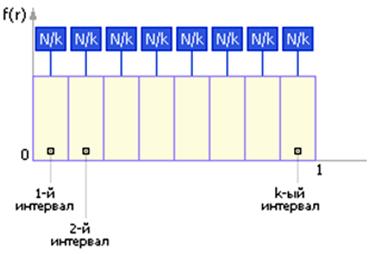
Рис. 1. Частотная диаграмма реального ГСЧ.

Реальный ГСЧ будет генерировать числа, распределенные по k интервалам, и в интервал попадет по n_i чисел [1]. Нужно рассмотреть квадраты разностей между полученным количеством чисел n_i и «эталонным» p_i · N. Слаживая их, в результате получим:

 χ²_эксп. = (n₁ – p₁ · N)² + (n₂ – p₂ · N)² + … + (n_k – p_k · N)².

Чем меньше разность в каждом из слагаемых, тем сильнее закон распределения случайных чисел, генерируемых реальным ГСЧ, тяготеет к равномерному [1]. В предыдущем выражении каждому из слагаемых приписывается одинаковый вес; для статистики «хи-квадрат» необходимо провести нормировку каждого i-го слагаемого, поделив его на p_i · N:

Наконец, полученное выражение более компактное уравнение:

Так можно получить значение критерия «хи-квадрат» для экспериментальных данных.

Приемлемым считают p от 10% до 90%.

Если χ²_эксп. больше χ²_теор., то генератор не удовлетворяет требованию равномерного распределения, так как полученные значения n_i очень отличаются от теоретически допустимых p_i · N и не могут рассматриваться как случайные [1]. Устанавливается большой доверительный интервал, в котором ограничения на числа становятся очень нежесткими, требования к числам — слабыми. При этом будет наблюдаться очень большая абсолютная погрешность.

Литература

1.                  http://csrc.nist.gov/publications/PubsSPs.html «DRAFT - SP800-90b».

Поступила в редакцию 11.10.2012 г.