Применение полиномов Чебышева при расчете коэффициента концентрации для трещин в однородной бесконечной (полубесконечной) упругой среде. Часть 2
Мовчан Игорь Борисович,
кандидат геолого-минералогических наук, доцент Санкт-Петербургского государственного горного университета.
Трещина Гриффитса
Согласно [1], поле напряжений имеет разрыв в каждой вершине трещины, представляемой в виде эллиптического выреза в нагружаемой среде. Напряжения сжатия-растяжения прикладываются к бесконечно удаленным от трещины границам этой среды. Берега самой трещины считаем ненагруженными. Процесс роста трещины представляет как увеличение семейства софокусных эллипсов. На каждом этапе роста трещина представляется в виде линии дислокаций (краевых – в случае плоского сжатия-растяжения, винтовых – в случае сдвиговой нагрузки). При обходе вокруг этой линии вектор смещения имеет конечное приращение – вектор Бюргерса b:
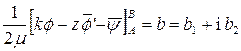 (2.1)
(2.1)
Существование, например, краевых дислокаций не приводит к дополнительным нагрузкам:
![]() , (2.2)
, (2.2)
где
![]() ,
, ![]() – комплексные
потенциалы, связанные с компонентами поля напряжений:
– комплексные
потенциалы, связанные с компонентами поля напряжений:
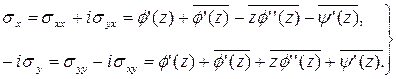 (2.3)
(2.3)
Объединим (2.1) и (2.2):
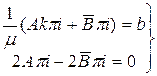 =>
=>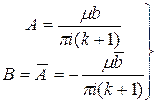 (2.4)
(2.4)
Для единичной дислокации, размещенной в начале координат:
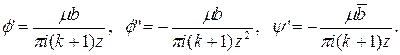 (2.5)
(2.5)
Пусть эта дислокация помещена в произвольную точку комплексной плоскости, тогда
![]()
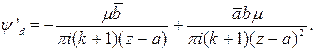 (2.6)
(2.6)
Тогда согласно (2.3) в окрестности единичной дислокации справедливо:
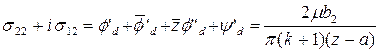 . (2.7)
. (2.7)
Для
простоты положим, что большая полуось эллиптического выреза расположена вдоль
вещественной оси, т.е. ![]() – координата дислокации
– координата дислокации ![]() - чисто вещественная, а
вектор Бюргерса имеет лишь мнимую составляющую
- чисто вещественная, а
вектор Бюргерса имеет лишь мнимую составляющую ![]() . Рассматривая линию краевых дислокаций вместо
одной, перепишем (2.7) в виде интегрального соотношения:
. Рассматривая линию краевых дислокаций вместо
одной, перепишем (2.7) в виде интегрального соотношения:
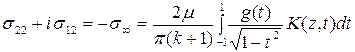 . (2.8)
. (2.8)
Заменой
переменных в (2.8) ![]() ,
где
,
где ![]() выводим
выводим
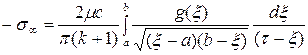 , (2.9)
, (2.9)
где
![]() - большая
полуось эллиптического выреза. Применим к (2.9) аппроксимационную формулу (1.28)
(Мовчан И.Б. «Аппроксимационный подход …», 2012), упрощая ее до вида,
известного в виде интегральной формулы Гаусса-Чебышёва:
- большая
полуось эллиптического выреза. Применим к (2.9) аппроксимационную формулу (1.28)
(Мовчан И.Б. «Аппроксимационный подход …», 2012), упрощая ее до вида,
известного в виде интегральной формулы Гаусса-Чебышёва:
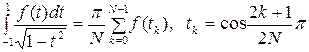 . (2.10)
. (2.10)
Объединяя (2.9) и (2.10), получим
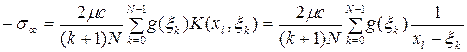 . (2.11)
. (2.11)
Здесь
![]() ,
, ![]() . (2.12)
. (2.12)
Для получения замкнутой системы линейных уравнений введем условие совместности, пригодное как трещины Гриффитса, так и для приповерхностной трещины:
![]() . (2.13)
. (2.13)
Это означает, что при обходе трещины по замкнутому контуру получаем нулевое приращение смещения. Рассматривая (2.10), (2.11) и (2.10), запишем
![]() . (2.14)
. (2.14)
Окончательно выводим следующую систему линейных уравнений:
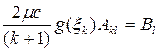 ,
,
где
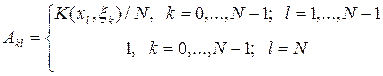 (2.15)
(2.15)
а
также 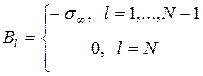 . (2.16)
. (2.16)
На основании формул (1.17.1), (1.17.2) (Мовчан И.Б. «Аппроксимационный подход …», 2012) запишем
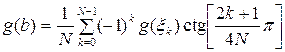 , (2.17.1)
, (2.17.1)
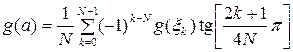 . (2.17.2)
. (2.17.2)
Для
вывода выражения коэффициента концентрации напряжений применим известное
теоретическое решение ![]() . Тогда, учитывая (2.17.1), (2.17.2) и (2.11),
имеем
. Тогда, учитывая (2.17.1), (2.17.2) и (2.11),
имеем
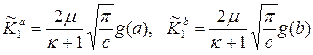 . (2.18)
. (2.18)
Например,
для концов единичной трещины ![]() формулы (2.18) дают
формулы (2.18) дают ![]() 0.1253D+01, что совпадает с
теоретическим решением для различных длин трещины Гриффитса. Последнее
демонстрирует правильность соотношений (2.18), которые применим теперь для
приповерхностной трещины и поверхностного выреза.
0.1253D+01, что совпадает с
теоретическим решением для различных длин трещины Гриффитса. Последнее
демонстрирует правильность соотношений (2.18), которые применим теперь для
приповерхностной трещины и поверхностного выреза.
Приповерхностная трещина
Предполагается
существование вертикальной границы раздела двух сред, причем в правой задана
краевая дислокация [2,3]. Среды слева от границы раздела соответствует
отрицательной полуоси ![]() ,
а справа – положительной. Условие непрерывности полей напряжений на границе
раздела приобретает форму:
,
а справа – положительной. Условие непрерывности полей напряжений на границе
раздела приобретает форму:
![]() . (2.19)
. (2.19)
Следовательно, на самой поверхности раздела:
![]() , (2.20)
, (2.20)
где индекс d определяет комплексные потенциалы краевой дислокации, а индекс 0 – комплексные потенциалы вмещающей среды. Простейшие преобразования (2.20) с объединением членов аналитических с правой и с левой стороны от поверхности раздела, получаем
![]() .(2.21)
.(2.21)
Поскольку поверхность раздела свободна от напряжений,
то ![]() , т.е.
, т.е.
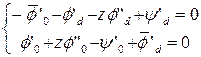 =>
=> 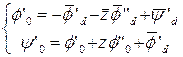 . (2.22)
. (2.22)
Комплексно сопряженные функции будут аналитическими
только при соблюдении условия ![]() . В этом случае
. В этом случае
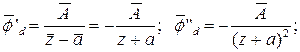
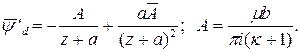 (2.23)
(2.23)
Тогда используя (2.22) для вывода ![]() и
и ![]() получаем следующие выражения:
получаем следующие выражения:
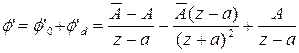 , (2.24)
, (2.24)
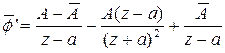 , (2.25)
, (2.25)
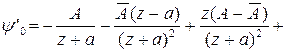
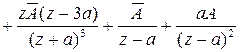 . (2.26)
. (2.26)
Причем в (2.25) условие ![]() более не применимо. Для проверки
справедливости (2.24)-(2.26) применим их при
более не применимо. Для проверки
справедливости (2.24)-(2.26) применим их при ![]() при стремлении z к границе раздела,
т.е. когда
при стремлении z к границе раздела,
т.е. когда ![]() ,
тогда как
,
тогда как ![]() -
произвольная. Тогда
-
произвольная. Тогда
![]()
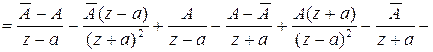
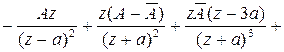
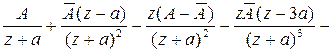
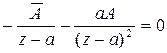 для любой точки на границе раздела. Таким
образом, формулы (2.24)-(2.26) верны. Используем их для вывода (2.8):
для любой точки на границе раздела. Таким
образом, формулы (2.24)-(2.26) верны. Используем их для вывода (2.8):
![]()
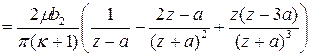 . (2.27)
. (2.27)
Аппроксимируя трещину линией краевых дислокаций и обращаясь вновь к (2.11), можем записать
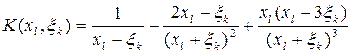 , (2.28)
, (2.28)
где ![]() и
и ![]() определяются формулой (2.12). Завершая
вывод системы линейных уравнений, как и в предыдущем случае, добавим условие
совместности (2.13) и дополнительное уравнение (2.14). Затем применим (2.15)-(2.18)
для получения коэффициента концентрации напряжений на левой и правой вершинах
горизонтальной приповерхностной трещины. Окончательно, мы можем рассчитать
безразмерную функцию F(c/d):
определяются формулой (2.12). Завершая
вывод системы линейных уравнений, как и в предыдущем случае, добавим условие
совместности (2.13) и дополнительное уравнение (2.14). Затем применим (2.15)-(2.18)
для получения коэффициента концентрации напряжений на левой и правой вершинах
горизонтальной приповерхностной трещины. Окончательно, мы можем рассчитать
безразмерную функцию F(c/d):
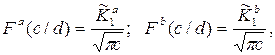 (2.29)
(2.29)
где d - наикратчайшее расстояние от границы раздела до центра трещины.
Поверхностный вырез
В рамках настоящей статьи имеется два аргумента к рассмотрению этой задачи:
· прослеживание изменения безразмерной функции F(c/d) в момент, когда приповерхностная трещина выходит на границу раздела, становясь поверхностным вырезом [4];
· проверка выводов в (2.27) и (2.28) при сравнении приблизительных значений коэффициента концентрации напряжений на вершинах трещины со значениями этого коэффициента, полученными из теоретической формулы
![]() . (2.30)
. (2.30)
Здесь
![]() - длина
большой полуоси эллиптического выреза (длина всей трещины) или расстояние от
границы раздела (свободной поверхности) до вершины трещины. Отличие от
приповерхностной трещины в том, что условие совместности (2.13) более не применимо.
Рассматривая случай раскрытия трещины в виде круглой дырки, возможно поместить
одну дислокацию внутрь нее для компенсации процесса раскрытия. Математически
это означает:
- длина
большой полуоси эллиптического выреза (длина всей трещины) или расстояние от
границы раздела (свободной поверхности) до вершины трещины. Отличие от
приповерхностной трещины в том, что условие совместности (2.13) более не применимо.
Рассматривая случай раскрытия трещины в виде круглой дырки, возможно поместить
одну дислокацию внутрь нее для компенсации процесса раскрытия. Математически
это означает:
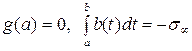 . (2.31)
. (2.31)
Составляя
алгоритм, прибегнем к (2.28) для получения коэффициентов ![]() линейных уравнений. Применяя
первое уравнение из (2.31) получим
линейных уравнений. Применяя
первое уравнение из (2.31) получим ![]() -е уравнение с коэффициентами, легко
выводимыми из (2.17.2):
-е уравнение с коэффициентами, легко
выводимыми из (2.17.2):
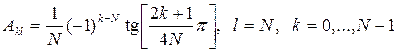 . (2.32)
. (2.32)
Затем
следует лишь использовать (2.16)-(2.18) для трещины, распространяющейся вглубь
материала. В результате получаем коэффициент концентрации напряжений как
функцию от ![]() и
функцию вида
и
функцию вида
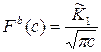 . (2.33)
. (2.33)
Можно
видеть, что ![]()
![]() и равна .119847D+00.
Справедливость данного результата подтверждается формулой (2.30).
и равна .119847D+00.
Справедливость данного результата подтверждается формулой (2.30).
Резюме
Нами рассмотрены аппроксимации трех классических в теории трещин случаев на основе ортогональных полиномов Чебышёва. Существование теоретических решений позволило подтвердить достоверность предложенных аппроксимаций. В качестве перспективы развития этой задачи сформулируем построение аналитической модели полей напряжений в вершине трещины, возникающей в периодическом и квазипериодическом композитах.
Литература
1. H.Liebowitz (ed.): Fracture. An advanced treatise. Vol.2, Mathematical Fundamentals. NY, 1968.
2. T.S.Cook, F.Erdogan: Stresses in bonded materials with a crack perpendicular to the interface. Int.J.Engineering Science., Vol.10, 1972, p.677.
3. D.O.Swenson, C.A.Rau: The stress distribution around a crack perpendicular to an Interface between Materials. Int.J.Fracture Mechanics, Vol.6, No4, 1970, p.357.
4. D.Nowell, D.A.Hills: Open cracks at or near free edges. J.Strain Analysis, 1987, Vol.22, p.177-185.
Поступила в редакцию 20.03.2012 г.