Об одном численном методе нахождения скоростей солитоновых волн в насыщенных пористых средах
Байрамова Нигяр,
диссертант Института прикладной математики,
Бакинский государственный университет.
On Nonlinear Waves Evolution in Porous Media at Two-Phase turation
Nigar Bayramli,
PhD Student Institute of Applied Mathematics of Baku State University.
Рассматривается численное решение нелинейного уравнения, описывающего распространения нелинейных волн в двухфазных континуумах. При этом, переходя в подвижную систему координат, с изменением масштаба времени и пространства, исследуется эволюция волны от источника возмущения. В первом приближении получено дисперсионное уравнение для скорости стационарно бегущих линейных волн, во втором приближении – нелинейное уравнение эволюции, мера эффект нелинейности которого сильно зависит от скорости дисперсии волн, диссипации энергии, реологии твердых частиц и силы межфазного взаимодействия. Первое уравнение решается как система линейных алгебраических уравнений. Используя метод конечных разностей и решение первой задачи, решается второе уравнения.
Ключевые слова: солитоновые волны, аппроксимация, пористая среда.
Nonlinear waves evolution in porous medium with two-phase pore filling has been created. Changing time and place scale with the help of the moving coordinating system waves evolution spread from vibrated and impulse reservoir is explored. In the first approximation a dispersed equation for linear waves at various velocities and in the second approximation the nonlinear equation of evolution are derived. The dependences of wave propagation on the velocity of dispersion, the dissipation of energy, the theology of sandstones and interphase resistance is shown. The first equation is solved as a system of linear algebraic equations. Using finite difference method and the decision of the first task, solved the second equation.
Keywords: solitonovye wave, approximation, porous medium.
1. Введение
При распространении волн с бесконечно малой амплитудой на земной коре, вместе ними могут возникать нелинейные волны с конечной амплитудой. В зависимости от состава пористой среды нелинейные волны, создаваемые источником возмущения, могут трансформироваться на близкие и дальние расстояния. Среди нелинейных волн существует такие волны, которые распространяются на дальние расстояние без изменения формы. Существование таких волн в земной коре доказано геофизическими наблюдениями. Нелинейные волны содержат больше информации, чем линейные волны. Среди них наибольший интерес представляют изолированные, т.е. солитоновые волны.
Основную долю многофазных пористых сред составляет скелет, а меньшая – насыщена газожидкостной смесью или одной из этих фаз. В рассматриваемой задаче средой является твердая среда, насыщенная водой. В работах [1, 2] Т.Рамазановым рассмотрена в разных средах задача трансформации волн во время возмущений. В этих работах показано, что если фазы многофазной пористой среды находятся в относительном покое, то в зависимости от реологии насыщенной пористой среды возмущения могут распространятся солитоновыми волнами. Эти конечно амплитудные волны, которые распространяют большие энергии, ускоряют разрушение среды. Аналогичные задачи рассматривались в работах [3, 4].
2. Постановка задачи
Для математической формулировки задачи даются уравнение неразрывности среды
![]() , (1)
, (1)
уравнение движения среды
![]() , (2)
, (2)
закон реологической деформации
![]() , (3)
, (3)
уравнение термодинамического состояния
![]() , (4)
, (4) ![]() концентрация среды.
концентрация среды.
Система (1)-(4) замыкается кинематическим соотношением
![]() , (5)
, (5)
Здесь i=1
относится твердой фазе, i=2 жидкой фазе; ![]() -соответственно средняя плотность и
скорость твердой и жидкой фаз;
-соответственно средняя плотность и
скорость твердой и жидкой фаз; ![]() ,
,![]() -давление в жидкой фазе,
-давление в жидкой фазе, ![]() -истинное напряжение в
твердой фазе;
-истинное напряжение в
твердой фазе; ![]() -пористость
среды;
-пористость
среды; ![]() -деформация
твердой фазы;
-деформация
твердой фазы; ![]() -определенные
константы конкретных самоэластичных жидкостей;
-определенные
константы конкретных самоэластичных жидкостей; ![]() - коэффициент расширения
- коэффициент расширения ![]() , или разжимания
, или разжимания ![]() ,
,![]() -единичный тензор.
-единичный тензор.
3. Решение задачи
Система уравнений (1)-(5) рассматривается в движущийся координатной системе и принимаются новые параметры
![]() , (6)
, (6)
Учитывая эти параметры систему (1)-(5) можно преобразовывать в следующем виде [5-7]:
![]() , (7)
, (7)
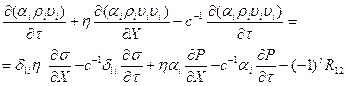 , (8)
, (8)
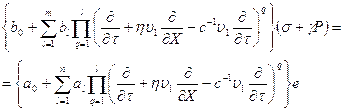 , (9)
, (9)
![]() , (10)
, (10)
Представим
искомые переменные в виде рядов по малому параметру ![]() <<1.
<<1.
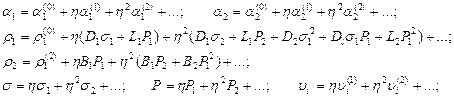 (11)
(11)
где
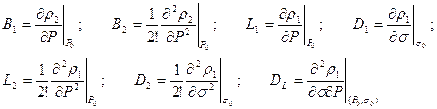 , (12)
, (12)
где ![]() и
и ![]() -значения концентрации, давления
и эффективного напряжения в неподвижном двухфазном континууме:
-значения концентрации, давления
и эффективного напряжения в неподвижном двухфазном континууме: ![]()
Членов ![]() представим в виде
представим в виде
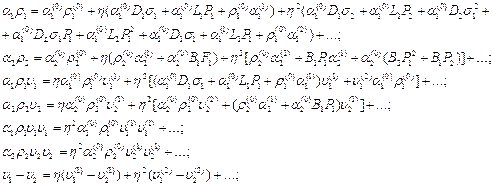 (13)
(13)
Если разложений
(11)-(13) подставим в систему уравнений (7)-(10) и приравниваем коэффициенты
членов с одинаковыми степенями ![]() в первом приближении получается система
однородных уравнений
в первом приближении получается система
однородных уравнений
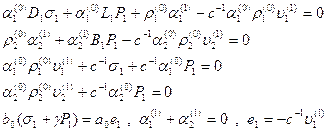 , (14)
, (14)
Система (14)
имеет нетривиальное решение, если ее детерминант обращается в нуль, что дает
следующее дисперсионное уравнение относительно скорости линейных волн -![]() :
:
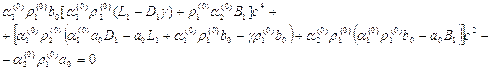 , (15)
, (15)
После обозначения
![]() =
=![]() ,
,
![]() =
=![]() , (16)
, (16)
![]() =
=![]() ,
,
![]() .
.
уравнение (15) получается в следующем виде
![]() , (17)
, (17)
Для среде камень-жидкость в уравнение (17) примем следующие данные:
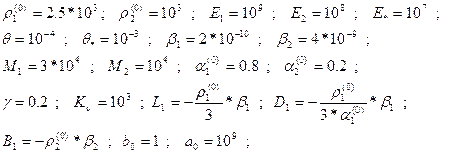 , (18)
, (18)
Учитывая эти
оценки в уравнении (17) скорость солитоновых волн получается: ![]() и
и ![]() .
.
Во второй приближении получается нелинейное эволюционное уравнение
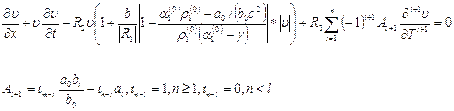 (19)
(19)
где
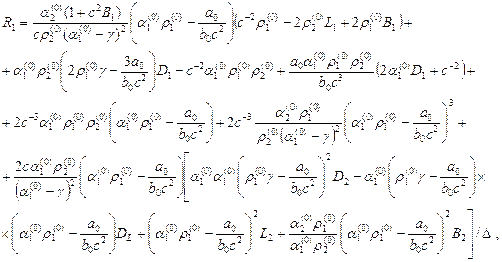
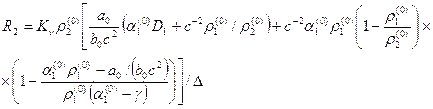
![]()
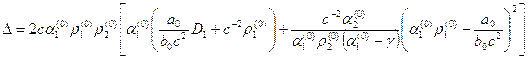
Уравнение (19) решается численным методом при следующих начальном и граничных условиях (n=2):
![]() , (20)
, (20)
![]() , (21)
, (21)
![]() , (22)
, (22)
![]() , (23)
, (23)
Для решения уравнения (21)-(23) используется метод конечных разностей или метод сеток [8]. Задача рассматривается в конечной области
G={![]() }
}
4. Аппроксимация
Разобьем ![]() на m равных
частей длины
на m равных
частей длины ![]() ,
а
,
а ![]() на n равных
частей длины
на n равных
частей длины ![]() .
Множество этих точек называется равномерной сеткой и обозначается
.
Множество этих точек называется равномерной сеткой и обозначается
![]()
Аппроксимурием дифференциальные операторы в форме
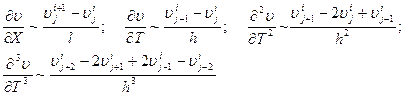 , (24)
, (24)
начальные и граничные условия (21),(22),(23) в форме
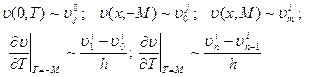
После аппроксимации уравнение (20) имеет вид:
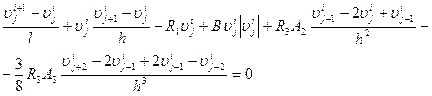 , (25)
, (25)
или
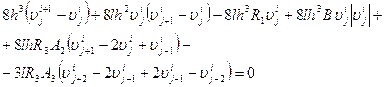
Отсюда
получаем значение для ![]()
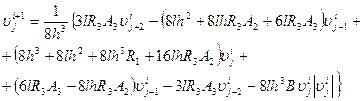 , (26)
, (26)
Уравнение (27) решается при следующих начальных данных:
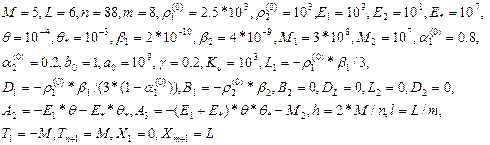 , (27)
, (27)
Решение
задачи (26) определено при ![]() и
и ![]() , результаты показаны в виде графика (рис.
1).
, результаты показаны в виде графика (рис.
1).
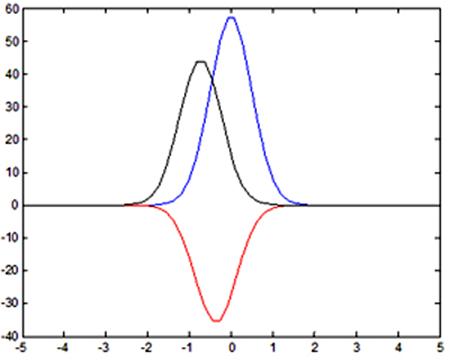
Рис. 1.
Литература
1. Рамазанов Т.К. Нелинейные волны в двухфазных системах// Прикладная механика, International Applied Mechanics.- Киев.- 1995.- том 31.- N8.- 1995.-С.38-45.
2. Рамазанов Т.К., Курбанов А.И. Математическая модель эволюции нелинейных волн в пористых средах при двухфазном насыщении // Труды ИММ АН Азербайджана .-Том IX(XVII).- 1998.- С. 157-166.
3. Шагапов В.Ш., Гималтдинов И.К., Галимзянов М.Н. Двумерные волны давления в жидкости, содержащей пузырьки // Механика жидкости и газа.- №2.- 2002.- С.139-147.
4. Ильичев А.Т. Уединенные волны в моделях гидромеханики. –М.:Физматлит, 2003.- 256 с.
5. Ramazanov T.K., Kurbanov A.I., Askerov T.M. Nonlinear waves in micrononequilibrium porous medium at two-phase saturation. Proceedinqs of Ion oflu // MM of NAS of Azerbaijan..- 2004.-XX(XXVIII),- Р.173-182.
6. Ramazanov T.K. On unequal solvabilitu of the evolutionary KdVRD equation. Solutions. // The Second International Conference. Tools for mathematical modeling. June 14-18. Book of abstracts.- Sank-Petersburg.1999,- P.115-116.
7. Самарский А.А.. Введение в численные методы.- Москва: Наука,1982.- 284 с.
Поступила в редакцию 08.06.2012 г.