Нелинейные колебания токонесущей ортотропной оболочки в переменном магнитном поле
Индиаминов Равшан Шукурович,
кандидат физико-математических наук, доцент,
Дониёров Абдирашид Абдирасулович,
магистрант.
Самаркандский филиал Ташкентского университета информационных технологий.
В работе построена нелинейная двумерная модель магнитоупругости токонесущей оболочки с учетом конечной ортотропной электропроводностью, магнитной и диэлектрической проницаемости. Проводится анализ электромагнитных эффектов и напряженно–деформированное состояние токонесущей ортотропной оболочки с учетом ортотропной электропроводности.
Ключевые слова: оболочка, магнитное поле, магнитоупругость.
A two-dimensional variant of connected nonlinear equations of electrodynamics of the current - carrying orthotropic rotation shells, under no stationary loads in presented. A procedure for solution of asymmetrical problems of magneto elasticity of flexible current-carrying orthotropic rotation shells under no stationary actions of mechanical and electromagnetic forces is plotted. A stress-strained state of flexible current-carrying orthotropic rotation shells in geometrically nonlinear statement.
Keywords: shell, magnetic field, magneto elasticity.
Развитие теории сопряженных полей и, в частности, теории электромагнитного взаимодействия с деформируемой средой считается одним из главных направлений развития современной механики твердого тела. Механизм взаимодействия упругой среды с электромагнитным полем разнообразен и обусловлен геометрическими характеристиками и физическими свойствами рассматриваемого тела. В частности, этот механизм получает некоторые специфические особенности, когда рассматриваем проблемы относительно тонких пластин и оболочек, обладающих анизотропной электропроводностью.
В большинстве работ взаимодействие упругого тела с электромагнитным полем рассматривается без учета анизотропной электропроводностью, магнитной и диэлектрической проницаемости. Когда материал проводящего упругого тела обладает свойством анизотропной электропроводностью, магнитной и диэлектрической проницаемости, то картина взаимодействия полей значительно усложняется и поэтому создания упрощенной, нелинейной теории магнитоупругого взаимодействия с учетом анизотропной электропроводностью, магнитной и диэлектрической проницаемости представляет научный интерес, как сточки зрения теории, так и приложений.
Задачи электромагнитоупругости анизотропных пластин и оболочек обладающей анизотропной электропроводностью представляет научный интерес. Дело в том, что в случае тонких анизотропных или изотропных тел с анизотропной электропроводностью можно ставить и решать оптимальные задачи магнитоупругости путем вариации всех физико-механических параметров материала тела. В частности, при постоянных механических и геометрических параметрах задачи, с помощью изменения анизотропных электродинамических параметров можно получить конструктивные элементы с качественно новым механическим поведением. Отметим, что в последнее время созданы материалы и наноматериалы с новыми электромагнитными свойствами. Эти материалы могут эффективно использоваться в различных областях новой техники при разработке новых технологий.
Нелинейная постановка задачи.
Будем рассматривать
гибкие токонесущие конические оболочки переменной вдоль меридиана толщины,
находящихся под действием нестационарных электромагнитных и механических полей.
Пренебрегая влиянием процессов поляризации и намагничивания, а также
температурными напряжениями считаем, что к торцу оболочку подводится переменный
электрический ток от внешнего источника. Предполагается, что сторонний электрический
ток в невозмущенном состоянии равномерно распределен по телу (плотность тока не
зависит от координат). Упругие свойства материала оболочки считаются ортотропными,
главные направления, упругости которого совпадают с направлениями соответствующих
координатных линий, электромагнитные же свойства материала характеризуются
тензорами электрической проводимости 
, магнитной проницаемости 
, диэлектрической
проницаемости 
.
При этом, исходя из кристаллофизики, для рассматриваемого класса проводящих
ортотропных сред с ромбической кристаллической структурой считаем, что тензоры 
, 
и 
принимают диагональный вид. В этом случае
произвольная поверхность второго порядка обладает тремя взаимно
перпендикулярными осями второго порядка и можно расположить эти оси параллельно
кристаллографическим осям второго порядка, а также характеристическая поверхность
второго порядка обладает всеми элементами симметрии, которые могут быть у
классов орторомбической системы. Предположим, что геометрические и механические
характеристики тела таковы, что для описания процесса деформирования применим
вариант геометрически нелинейной теории тонких оболочек в квадратичном
приближении. Также предполагаем, что относительно напряженности электрического
поля 
и
напряженности магнитного поля 
выполняются электромагнитные гипотезы [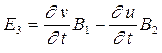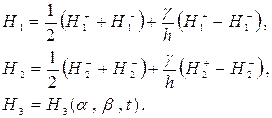1]:
, 
, 
,
(1)
Эти допущения являются некоторым
электродинамическим аналогом гипотезы недеформируемых нормалей и вместе с
последней составляют гипотезы магнитоупругости тонких тел. Принятие этих
гипотез позволяет свести задачу о деформации трехмерного тела к задаче о
деформации выбранной произвольным образом координатной поверхности. Координатную
поверхность в недеформированном состоянии отнесем к криволинейной ортогональной
системе координат 
и
, где 
длина дуги образующей
(меридиана), отсчитываемая от некоторой фиксированной точки, 
центральный угол в параллельном
круге, отсчитываемый от выбранной плоскости. Координатные линии 
и 
являются линиями главных кривизн
координатной поверхности. Выбирая координату 
по нормали к координатной поверхности
вращения, относим оболочки к координатной пространственной системе координат 
. Предполагаем, что на
поверхности конической оболочки известен вектор магнитной индукции, а также
поверхностные механические силы.
При получении
разрешающей системы в нормальной форме Коши выберем в качестве основных функций
Выбрав
именно эти функции, в дальнейшем можно выбирать различные комбинации
закрепления конуса. Дифференциальная система уравнений в основных функциях, описывающая
напряженно-деформированное состояние токонесущих оболочек в магнитном поле при
учете геометрической нелинейности и ортотропной электропроводностью,
разрешается относительно первой производной искомых функций по одной из
координат. Предполагаем, что все компоненты возбужденного электромагнитного
поля и поля перемещений входящие в уравнения задачи магнитоупругости не зависит
от координаты 
,
а также считаем, что упругие и электромагнитомеханические характеристики
материала оболочки не изменяются вдоль параллели. После некоторых преобразований
[2] получаем полную систему нелинейных дифференциальных уравнений
магнитоупругости в форме Коши, которая описывает напряженно-деформированное
состояние токонесущей ортотропной конической оболочки при нестационарном
воздействии механического и магнитного полей.
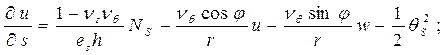
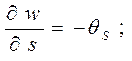
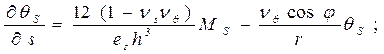
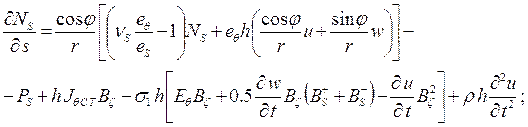(2) 
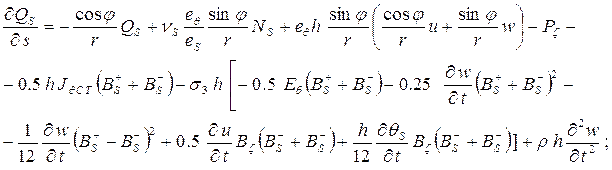
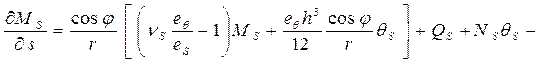
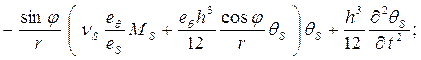
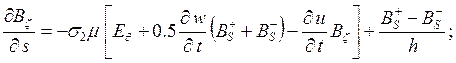
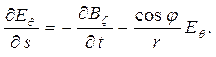
В соотношениях (1), (2)
использованы общепринятые в теории оболочек и теории электромагнитоупругости
обозначения. Кроме того, здесь введены такие обозначения: 
- тангенциальные составляющие
индукции магнитного поля на поверхностях токонесущей конической оболочки.
Решение краевых задач магнитоупругости связано с определенными трудностями. Это
объясняется тем, что разрешающая система (2) является системой дифференциальных
уравнений гиперболо-параболического типа восьмого порядка с переменными
коэфициентами. Компоненты пондеромоторной силы Лоренца включают нелинейные члены,
обусловленные учетом перемещений оболочки при ее деформировании.
Разработанный методики к численному решению новых класс связанных задач магнитоупругости теории ортотропных конических оболочек вращения обладающей ортотропной электропроводностью, основан на последовательном применении конечноразностной схемы Ньюмарка, метода квазилинеаризации и дискретной ортогонализации [2, 3, 4, 5].
Для
эффективного использования предложенной методики предполагаем, что при
появлении внешнего магнитного поля не возникает резких скин-эффектов по толщине
оболочки и электромагнитный процесс по координате 
быстро выходит на режим, близкий к
установившемуся. Отметим что, применяя схему Ньюмарка, весь интервал изменения
времени разобьем на отдельные малые по времени интервалы и историю деформирования
проследим, последовательно решая задачи на каждом временном слое.
В качестве
примера рассматриваем нелинейное поведение ортотропной токонесущей конической
оболочки переменной толщины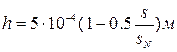 
. Считаем, что оболочка из бериллия
находится под воздействием механической силы 
, стороннего электрического тока 
и внешнего магнитного
поля 
, а также
что оболочка имеет конечную ортотропную электропроводность 
. Сторонний электрический ток в
невозмущенном состоянии равномерно распределен по оболочке, т.е. плотность
стороннего тока не зависит от координат.
Исследуем поведение ортотропной оболочки переменной толщины в зависимости от изменения стороннего электрического тока, который изменяется следующим образом (5 вариантов):
; 
; 
;
; 
Граничные условия:
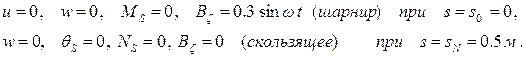
Параметры оболочки и материала принимаем следующими:
, 
, 
, 
, 
,
, 
, 
, 
,
,
,
, 
, 
, 
, 
,
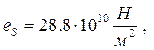
Решение
задачи определено на интервале времени 
, шаг интегрирования по времени выбирался
равным 
.
Максимальные значения получены при шаге по времени 
. Отметим, что в ррассматриваемом
случае анизотропия удельного электрического сопротивления равно 
.
На ниже приведенных рисунках графики (1, 2, 3, 4, 5) соответствуют следующим вариантам изменения стороннего электрического тока:
1.
; 2.
; 3.
; 4.
; 5. 
.
На рис. 1
дано распределения максимальных значений напряжений 
внутренней поверхностях оболочки
в зависимости от времени при 
для всех вариантов изменения стороннего
электрического тока 
.
Из рис. 1 следует,
что увеличение значения стороннего электрического тока приводит к увеличению
значения напряжений оболочки и их максимальные значения возникают в окрестности
точки при 
.
На рис. 2
приведено изменение магнитной индукции 
по длине оболочки при для всех вариантов изменения
стороннего электрического тока 
.
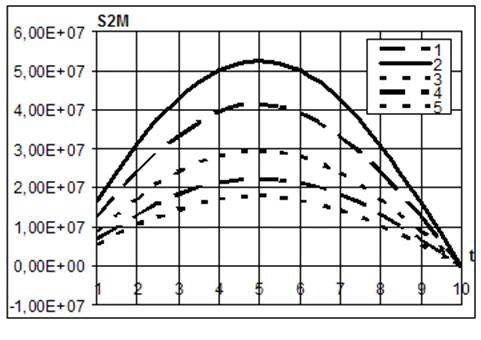
Рис. 1. Распределение напряжений 
по внутренней поверхности
оболочки в зависимости от времени при для всех вариантов изменения стороннего
электрического тока 
.
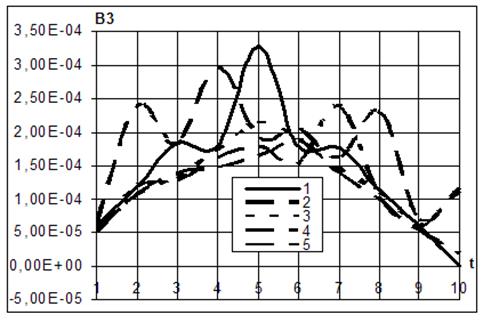
Рис. 2. Изменение магнитной индукции 
в зависимости от
времени при для
всех вариантов изменения стороннего электрического тока .
Как видно из рисунков, с увеличением значений стороннего электрического тока значения напряжений оболочки и магнитной индукции увеличиваются.
Приведенные результаты дают возможность оценить влияние на оболочку внешнего электрического тока и магнитной индукции, а также их комбинированное воздействие.
Таким образом, выбирая направленность и величину плотности стороннего электрического тока, можно оптимизировать напряженное состояние оболочки.
Литература
1. Амбарцумян С.А., Багдасарян Г.Е., Белубекян М.В. Магнитоупругость тонких оболочек и пластин. - Москва: Наука, 1977. - 272 с.
2. Indiaminov R.SH., Mol`chenko L.V., Loss. I.I. The magnetoelastisity of conical shells mith ortotropic elektroconductivity in nonlinear position // Bulletin of the University of Kiev. Series: Physics & Mathematics.-2007. N.2. P.85-90.
3. Indiaminov R.SH., Mol`chenko L.V., Loss. I.I. Determining the Stress State of Flexible Orthotropic Shells of Revolution in Magnetic Field //International Applied Mechanics.-2008.-Vol. 44. No.8. P.882 - 891.
4. Indiaminov R.SH. On the absence of the tangential projection of the Lorenz force on the ax symmetrical stressed state of current-carrying conic shells // International Journal Computational Technologies 2008. - Vol.13. N.6. P. 65 - 77.
5. Индиаминов Р.Ш. Решение связанных динамических задач магнитоупругости токонесущих ортотропных конических оболочек // Сборник статьей Одиннадцатой междунар. научно-практ. конф. «Фундаментальные и прикладные исследования, разработка и применение высоких технологий в промышленности». 27-29 апреля 2011 г., г. Санкт-Петербург, Россия. Т. 3. - Санкт-Петербург, 2011. - С: 152-158.
Поступила в редакцию 10.09.2012 г.