Использование симметричных и несимметричных операционных усилителей для реализации активных RC-фильтров
Ержан Асел Ануаркызы,
докторант Казахского национального технического университета им. К. И. Сатпаева, г. Алматы.
Основные преимущества симметричных операционных усилителей по сравнению с несимметричными заключается в возможности комбинации в широких пределах положительной и отрицательной обратной связей и наличии двух достаточно хорошо развязанных путей передачи сигнала.
Вначале рассмотрим модели, где используется операционный усилитель с симметричным входом и несимметричным выходом. На рисунке 1 изображена модель реализации на основе ОУ с симметричным входом в сочетании с RC-пятиполюсником.
При ![]() передаточная функция напряжения имеет
вид [1]:
передаточная функция напряжения имеет
вид [1]:
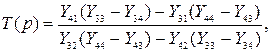 (1)
(1)
где ![]() – элемент матрицы
проводимостей пассивного RC-пятиполюсника. С
помощью такой модели возможно реализовать передаточную функцию n-го порядка с
произвольным расположением нулей на плоскости комплексного переменного. Общей
методике реализации схем по модели (см. рисунок 1) по заданной передаточной
функции
– элемент матрицы
проводимостей пассивного RC-пятиполюсника. С
помощью такой модели возможно реализовать передаточную функцию n-го порядка с
произвольным расположением нулей на плоскости комплексного переменного. Общей
методике реализации схем по модели (см. рисунок 1) по заданной передаточной
функции ![]() в настоящее время не существует [2].
в настоящее время не существует [2].
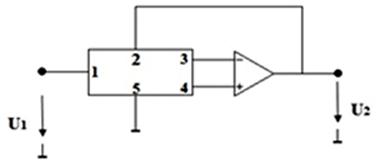
Рис. 1. Модель реализации на основе ОУ с симметричным входом в сочетании с пассивным RC – пятиполюсником.
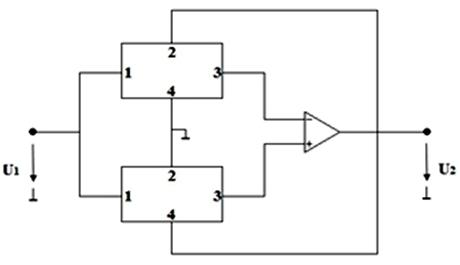
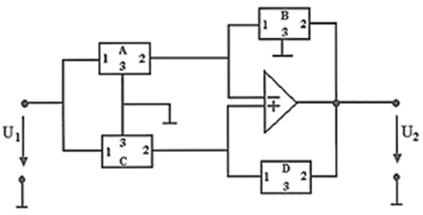
Рис. 2. Модель реализации на основе ОУ с симметричным входом а) в сочетании с двумя RC-четырехполюсниками; б) в сочетании с двумя RC- трехполюсниками.
На основе модели (см. рисунок 1) можно получить ряд вариантов, позволяющих упростить синтез пассивного RC-пятиполюсника. Путем разбиения RC-пятиполюсника на две четырехполюсника, получим модель, представленную на рисунке 2. а и имеющую передаточную функцию напряжения вида
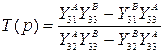 , (2)
, (2)
где ![]() – элементы матриц проводимостей
соответствующих RC-
четырехполюсников.
– элементы матриц проводимостей
соответствующих RC-
четырехполюсников.
На рисунке 2,б приведена модель, которая получается из предыдущей модели представлением каждого четырехполюсника в виде двух RC- трехполюсников. Передаточная функция напряжения этой модели
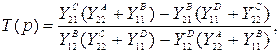 (3)
(3)
где ![]() - элементы матриц проводимостей
соответственно А, В, С и D-трехполюсников
[1].
- элементы матриц проводимостей
соответственно А, В, С и D-трехполюсников
[1].
Согласно [2], общих методов синтеза пассивных цепей этих моделей в настоящее время не существует. В литературе излагаются лишь конкретные способы реализации простых передаточных функций.
Cхема на рисунке 3 позволяет реализовать амплитудно-частотную характеристику фильтра второго порядка низкочастотного (ФНИЧ), высокочастотного (ФВЧ) и полосового (ПФ) типов. Несмотря на то, что эту схему можно рекомендовать только в случае малых устройствах связи
Тонкопленочные резисторы и конденсаторы, необходимые для реализации любой функции второго порядка схемой рисунок 4, изготавливают на поверхности подложки. Имеются токопроводящие дорожки цепи обратной связи для всех вариантов и по необходимости они размыкаются. Получить любую цепь второго порядка можно, удалив каким-нибудь способом (срезом, скрайбированием или травлением) соответствующие компоненты и соединением.
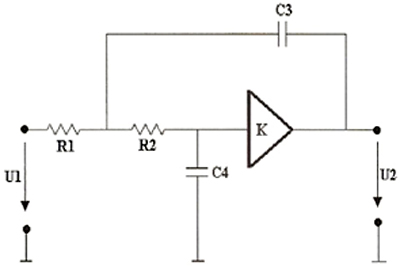
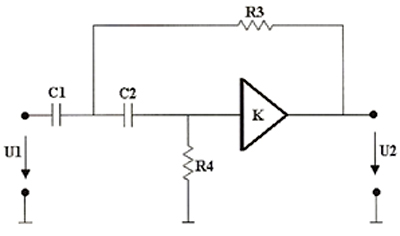
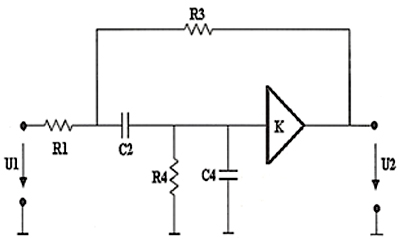
Например, удалив C1, С2 и R3, можно получить фильтр нижних частот (см. рисунок 4, а), R2, R1и СЗ 9 фильтр верхних частот (см. рисунок 4, б), R2, С1 и С2 - полосовой фильтр (см. рисунок 4, в).
Запишем функцию передачи с комплексными
полюсами ![]()
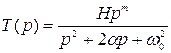 , (4)
, (4)
где Н - постоянный множитель;![]() m = 0, 1,2.
m = 0, 1,2.
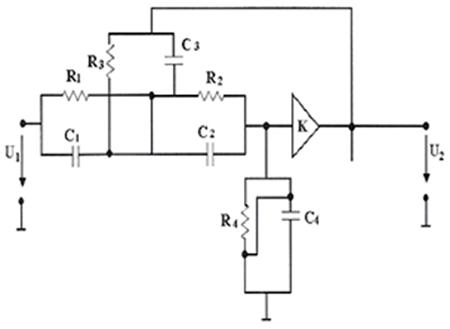
Рис. 3. Схема унифицированного блока 2-го порядка.
а)
б)
в)
Рис. 4. Схема ФНЧ 2-го порядка (а). Схема ФВЧ 2-го порядка (б). Схема ПФ 2-го порядка (в).
Если ![]() , то функция (4) определяет функцию
передачи фильтра нижних частот с собственной частотой
, то функция (4) определяет функцию
передачи фильтра нижних частот с собственной частотой ![]() и добротность
и добротность ![]()
При ![]() получим полосовой фильтр,
получим полосовой фильтр, ![]() – фильтр верхних частот. Для схемы
нижних частот (см. рисунок 4,а):
– фильтр верхних частот. Для схемы
нижних частот (см. рисунок 4,а):
![]() (5)
(5)
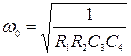 (6)
(6)
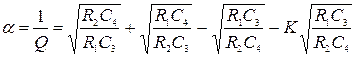 (7)
(7)
Для фильтра верхних частот (см. рисунок 4, б):
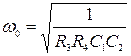 (8)
(8)
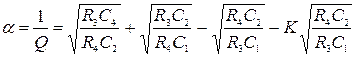 (9)
(9)
Для полосового фильтра (см. рисунок 4, в):
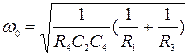 (10)
(10)
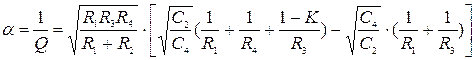 (11)
(11)
Параметры этих схем можно регулировать.
Так, например, для фильтра нижних частот настройку на частоту ![]() можно производить резисторами R1 и R2 (или емкостями
СЗ и С4) при сохранении их отношения, чтобы не влиять на величину добротности.
Добротность можно регулировать изменением усиления К. Эти схемы при больших
добротностях обладают значительным диапазоном параметров схемных элементов и
высокими чувствительностями. Для достаточной стабильности характеристик
добротность Q
должна
быть меньше 10, что и препятствует широкому использованию этих схем.
можно производить резисторами R1 и R2 (или емкостями
СЗ и С4) при сохранении их отношения, чтобы не влиять на величину добротности.
Добротность можно регулировать изменением усиления К. Эти схемы при больших
добротностях обладают значительным диапазоном параметров схемных элементов и
высокими чувствительностями. Для достаточной стабильности характеристик
добротность Q
должна
быть меньше 10, что и препятствует широкому использованию этих схем.
Подведя итоги рассмотрения методов реализации с использованием несимметричного операционного усилителя, можно сделать выводы, что эти фильтры – наиболее детально исследованные элементы в теории активных RC-фильтров. Но необходимо учесть отсутствие таких схем, которые позволяют строить унифицированные звенья второго порядка.
По результатам исследования различных схем активных RC-фильтров с непосредственным использованием ОУ, видно, что схемы звеньев 2-го порядка с одним ОУ при больших добротностях обладают значительным диапазоном параметров схемных элементов, для большинства таких схем характерна высокая чувствительность.
С помощью аппроксимирующей цепи с низкой добротностью и активной корректирующей цепью, возможно реализация унифицированного звена второго порядка.
Литература
1. Хъюлсман Л.П. Теория и расчет активных RC-цепей. Перевод с англ. Под редакцией А.Е. Знаменского М., «Связь», 1973. 238 с.
2. Синтез активных RC-цепей. Современное состояние и проблемы. Под ред. Ланнэ А.А. М., «Связь», 1975. 296 с.
3. Ержан А.А., Жунусов З.А. Уравнения в гибридных координатных базисах. Сборник трудов // I-ая Международная научно-практическая конференция – 2010 г.-Алматы.- с.145-152.
Поступила в редакцию 24.04.2012 г.