Моделирование процесса прогрева углеродного материала

Безуглов Александр Михайлович,

доктор технических наук, профессор,

Безуглов Владимир Александрович,

соискатель.

Кафедра высшей математики, Южно-Российский государственный технический университет (Новочеркасский политехнический институт) им. Платова.

Решение задачи о прогреве углеродсодержащего материала базируется на теории теплопроводности Фурье. Получающееся в результате дифференциальное уравнения температуропроводности может быть решено в зависимости от начальных и граничных условий для образцов разной формы и размеров [1]. Как известно из стационарных решений, распределение температуры внутри образца существенно зависит от его формы, но не смотря на различия, в выражениях для температур, из них получаются близкие по смыслу и величине оценки времени прогрева: , где a² – температуропроводность, R – некоторый геометрический размер (радиус диска, шара) [2].

Реальные химические технологии включают процессы далеко отличающиеся от стационарных. Ниже приводятся результаты рассмотрения процессов прогрева в реальных условиях промышленной установки, изменяющихся с течением времени и по мере обработки, соответствующие краевые условия и уравнения имеют вид:

T(0, r) = T₀ – начальная температура,

 – поверхностная температура,

 – условия в центре образца.

, где .

Операционным методом было получено решение:

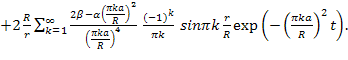
Последнее слагаемое становится малым при . При этом на поверхности r=R температура для любого момента времени t:

В центре образца r = 0, :

В результате, как показывают оценки для конкретных случаев - , температуры внутри образцов могут отличаться от поверхностных на сотни градусов (до 500⁰С). При этом общее выражение для разности температур поверхности и центра имеет вид:

где основной вклад дает первое слагаемое. Задержка прогрева как во времени, так и по температуре пропорциональна .

В условиях реального производства такая закономерность проявляется в сильной зависимости основных показателей производства – прежде всего, кпд и качества продукта - от неоднородности гран состава исходного материала. Поскольку основным действующим фактором изменения физико-химических свойств углеродного материала, является удельное количество поглощенного тепла. Оценим его с учетом найденной .

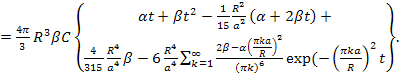
При условии , последнее слагаемое в Q исчезает, а первое, с точностью до множителя, совпадает с аналогичным для T(t,r):

Поэтому можно воспользоваться сделанными для T(t,r) оценками, и утверждать, что с ростом R удельное количество поглощенного тепла 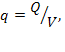может снижаться в несколько раз в сравнении со значением q для образцов малого радиуса(внутри допустимого грансостава).

В связи с этим возникает технологическая дилемма – повышать время и температуру термообработки, ужесточая процесс, или мириться со снижением качества вследствие недостаточности термообработки внутренних слоев крупных образцов. Поскольку показатели качества фиксированы или ограниченны допусками, то приходится идти на ужесточение процесса(при этом, всегда оказывается, что за время дообработки крупной фракции, мелкая пережигается, угорает, уносится и т.д., приводя к дополнительным потерям и снижает кпд процесса).

Если технологический процесс оптимизирован на обработку определенной фракции R₀ углеродного материала: подобраны время выдержки (процесса) и определен закон T=T(t,R₀), то в результате, получается качественный готовый продукт, при некотором достигнутом уровне кпд -. Образцы R<R₀ прогреваются раньше, следовательно, какое-то время предназначенная для них доля энергии улетает в трубу, тем самым снижается общий кпд. Часть материала-R>R₀ – прогревается частично, получает q<q₀ , при тех же общих затратах энергии. Следовательно, в определении полного кпд появляется еще один понижающий множитель, пропорциональный концентрации крупной фракции.

Представим q в более удобной форме: Откуда можно получить еще одно выражение:  - заданная температура, инвариантная технологическая величина, рассчитанная на эффективное производство оптимальных образцов  Вводя представление , для  получим выражение: Откуда  Определим кпд для оптимального образца , где  доля энергии, направленная на оптимальное нагревание частиц оптимального размера R₀, для неоптимальных размеров получим или . Кпд закономерно снижается.

Изменение знака , то есть наличие мелкой фракции к противоречию не приводит и коэффициент полезного действия не увеличивает, так как в этом случае включаются другие негативные процессы.

Таким образом в технологиях, где основным является процесс термообработки, ключевую роль играет оптимизация грансостава. Если из химических, физических, конструкционных и прочих соображений  выбирается в качестве «средней», «стандартной» и т.п. фракции технологического процесса, то одинаково важным является минимальное присутствие как крупной, так и мелкой фракций.

Полученные теоретические выводы можно проиллюстрировать результатами промышленных испытаний прокалочных печей: в результате комплексных мер по оптимизации грансостава технологического процесса удалось снизить потери на угар на 67%(то есть в 3 раза).

Литература

1.                  Безуглов А.М. Оптимизация прогрева антрацита в термопечах. Современные достижения в области исследования производства и эксплуатации углеродных материалов.- Тезисы докладов и сообщений Всесоюзной конференции молодых ученых и специалистов: Челябинск 1984.-С.42.

2.                  Посыльный В.Я., Безуглов А.М. Влияние неоднородностей грансостава на оптимизации. Процесса термообработки антрацитов. Высокотемпературные и плазмохимические процессы:Межвуз. сб. науч. тр. – Литиздат, 1987.-С.124-127.

Поступила в редакцию 18.02.2013 г.