Статистика технологических флуктуаций
Безуглов Александр Михайлович,
доктор технических наук, профессор,
Безуглов Владимир Александрович,
соискатель.
Кафедра высшей математики, Южно-Российский государственный технический университет (Новочеркасский политехнический институт) им. Платова.
В реальном
термодинамическом процессе флуктуации могут испытывать как координаты процесса,
так и термодинамические потенциалы и целевые функции. Для описания
термодинамического процесса (или состояния) достаточно выбрать ограниченное
число термодинамических координат и соответствующих им потенциалов, остальные параметры
являются функциями этих независимых аргументов [1]. Статистическое описание
независимых переменных производиться через их математическое ожидание и дисперсию.
Все прочие характеристики, являясь в общем случае нелинейными функциями,
зависят как от средних значений координат, так и от средних значений их
флуктуаций. Среднее значение некоторой статистической функции 
, распределенное по закону 
, определяется выражением [2]:
Поскольку заранее не известна, рассмотрим, в качестве
примера, два крайних случая.Предполагая 
распределенной
равномерно на 
, а 
разложимой в ряд Тейлора в окрестности 
получим:
Таким образом,
если 
положительно определена, то флуктуации (
) эффективно увеличивают
, если 
для 
и уменьшают, если 
. Аналогичные поправки связаны с высшими
производными четных порядков. Если - отрицательна, то для сохраняется те же утверждения, а для модуля 
справедливы противоположные. Полученные результаты
универсальны и, в известной степени, не зависят от способа усреднения.
Вычисления в случае нормального распределения приводят к
аналогичным результатам.
Следовательно,
можно утверждать, что дисперсия – D =
– флуктуирующего физического параметра определяет в
первом приближении смещение его функции 
от ее нулевого
приближения 
. Физический смысл полученных выражений состоит в
том, что нелинейные процессы реагируют изменением своих показателей на наличие
флуктуаций. Статистический подход, к оценке влияния флуктуаций позволяет
сделать некоторые общие выводы, имеющие отношение к произвольным
термодинамическим процессам, идущим с поглощением тепла. Если целевая функция
имеет область насыщения, то, как известно, условия 
означает убывающую функцию, с графиком обращенным
выпуклостью вниз, а 
– означает возрастающую функцию с выпуклостью,
обращенной вверх (линии 1 и 2 на рис. 1).
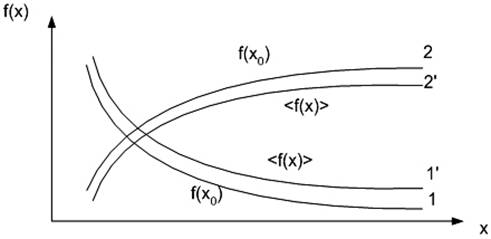
Рис.
1. Влияние флуктуаций на достижение целевой функцией 
оптимального значения.
Для таких
функций всегда будет справедливо утверждение: наличие флуктуаций негативно
сказывается на показателе и, следовательно, требуются дополнительные затраты
на достижение заданного результата (см. линии 
, 
, рис.1).
Для технологического процесса это означает повышение, прежде всего, энергозатрат (и, следовательно, снижение кпд). Таким образом важнейшим следствием присутствия флуктуаций параметров в технологическом процессе является появление понижающего его множителя в выражении для кпд (по некоторому актуальному параметру).
Наиболее выгодным с экономической точки зрения оказывается процесс без флуктуаций, для повышения эффективности производства необходимо принимать меры к снижению интенсивности флуктуаций технологических параметров.
Если функция такова, что она
возрастает, не имея области насыщения, то при наличие флуктуации приводит к ускоренному и
неограниченному росту. Однозначно можно утверждать, что таких флуктуаций не
существует в природе, если растет с ростом энергопотребления: существование их
противоречило бы закону сохранения энергии, флуктуации приводили бы к
энергетическим эффектам без энергопотребления, например, плавлению при 
.
Литература
1. Безуглов А.М., Кураков Ю.И. Математическое моделирование технологических процессов. Северо-Кавказкий научный центр высшей школы: Ростов-на-Дону 2002.-С.104.
2. Посыльный В.Я., Безуглов А.М. Влияние неоднородностей теплового поля на качество термоантрацита // Химия твердого топлива, 1986.-№ 1.-С. 103-104.
Поступила в редакцию 18.02.2013 г.